Find the focal length of lens shown in the figure. Solve for three cases nS=1.5,nS=2.0,nS=2.5.
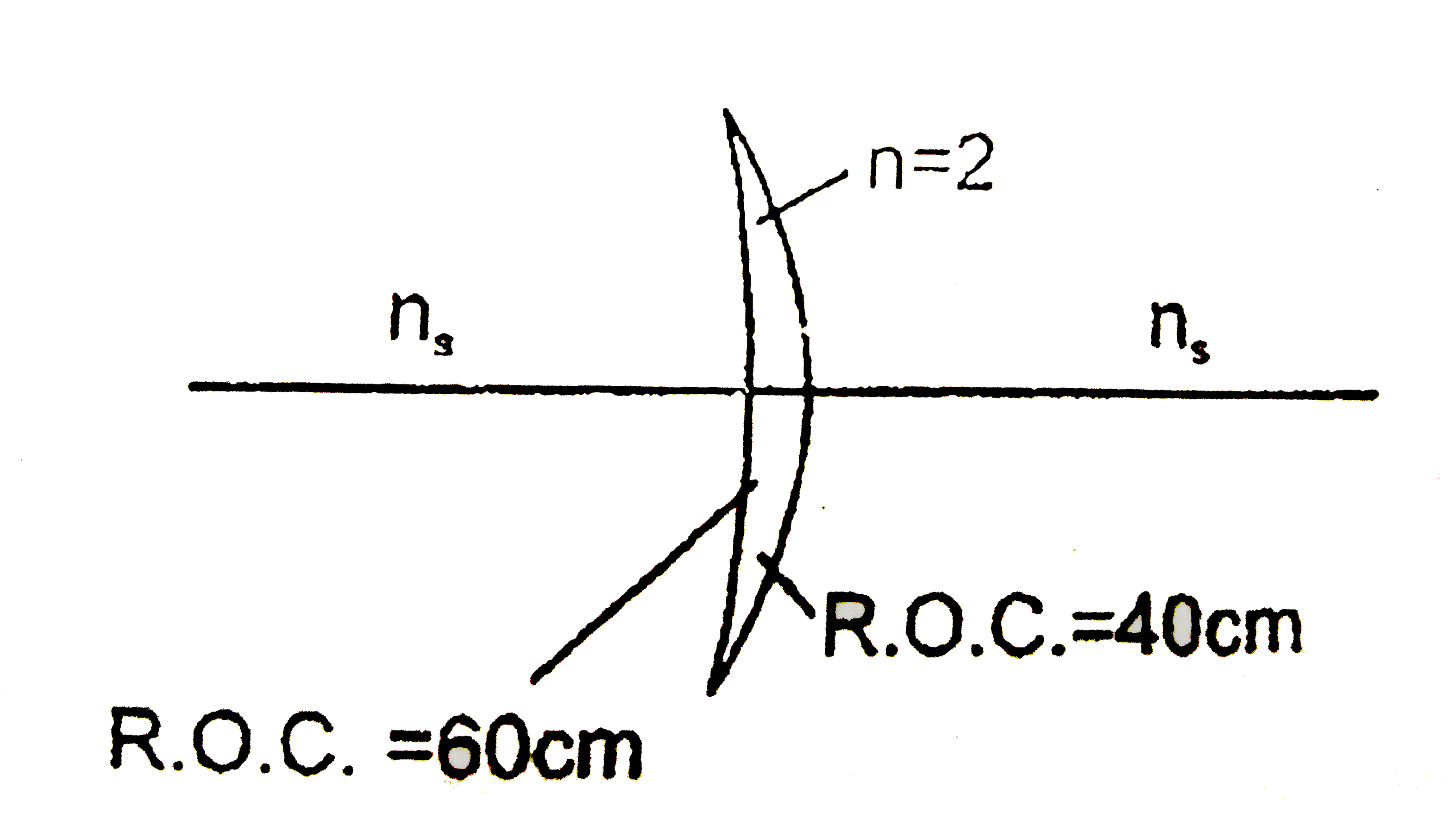
The correct Answer is:360cm,∞;−600cm
1f1=(21.5−1)(1−60−1−40)⇒f1=360cm
1f2=(22−1)(1−60−1−40)=0⇒f2=∞
1f3=(22.5−1)(1−60−1−40)⇒f3=−600cm
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-2
Explore 62 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Which of the following sets of quantum numbers represents the highest energy of an electron?
(A) n = 5, l = 0, m = 0, s = +1/2
(B) n = 6, l = 2, m = 1, s = +1/2
(C) n = 5, l = 1, m = 1, s = -1/2
(D) n = 4, l = 1, m = 0 s = -1/2
View SolutionFind the product of 72s2t and s+t. Verify the result for s=12and t=5.
View SolutionIf sum of n terms of a sequence is Sn then its nth term tn=Sn−Sn−1. This relation is valid for all n>−1 provided S0=0. But if S1=0, then the relation is valid ony for n≥2 and in that case t1 can be obtained by the relationt1=S1. Also if nth term of a sequence tn=Sn−Sn−1 then sum of n term of the sequence can be obtained by putting n=1,2,3,.n and adding them. Thus n∑n=1tn=Sn−S0. if S0=0,thenn∑n=1tn=Sn. On the basis of above information answer thefollowing questions: If nth term of a sequence is 1(n+2)n! then sum of to infinity of this sequence is (A) 1 (B) 12 (C) 13 (D) none of these
View SolutionLet S1,S2,S3, …. Are squares such that for each n≥1, The length of the side of Sn is equal to length of diagonal of Sn+1. If the length of the side S1 is 10 cm then for what value of n, the area of Sn is less than 1 sq.cm.
View SolutionIn an arithmetic series, if Sn=3n2+2n, find the first three terms.
View SolutionFrom the following sets quantum number state which are possible. Explain why the other are not permitted ?
a. n=0,l=0,m=0,s=+1/2
b. n=1,l=0,m=0,s=−1/2
c. n=1,l=1,m=0,s=+1/2
d. n=1,l=0,m=+1,s=+1/2
e. n=0,l=1,m=−1,s=−1/2
f. n=2,l=2,m=0,s=−1/2
g. n=2,l=1,m=0,s=−1/2
View SolutionTwo coherent monochromatic point sources S1 and S2 are placed in front of an infinite screen as shown in figure. Wavelength of the light emitted by both the sources is zero. Initial phase difference between the sources is zero.
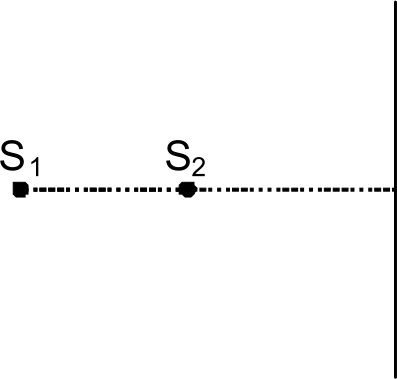
Initially S1S2=2.5λ and the number of bright circular rings on the screen in n1. if the distance S1S2 is increased and made 5.7λ, the number of bright circular rings becomes n2. the difference n2−n1 is
View SolutionIf C0,C1,C2,…,Cn denote the binomial
coefficients in the expansion of (1+x)n , then n∑0≤rn∑<s≤nCrCs=.
View SolutionIf Sn, be the sum of n terms of an A.P; the value of Sn−2Sn−1+Sn−2, is
View SolutionDesignate the electrons with the following sets of quantum numbers :
(a) n=3,l=0,m=0,s=−12
(b) n=2,l=1,m=+1,s=+12
(c ) n=5,l=0,m=0,s=+12
View Solution