An object of height 1cm is set at angles to the optical axis of a double convex lens of optical power 5D and 25cm away from the lens. Determine the focal length of the lens, the position of the image. The linear magnification of the lens, and the height of the image formed by it.
The correct Answer is:20cm,1m,−4,4cm
To solve the problem step by step, we will determine the focal length of the lens, the position of the image, the linear magnification, and the height of the image formed by the lens.
Step 1: Determine the Focal Length of the Lens
The power P of a lens is related to its focal length f by the formula:
P=1f
Given that the power of the lens is 5D, we can rearrange the formula to find the focal length:
f=1P=15=0.2 m=20 cm
Step 2: Determine the Position of the Image
We will use the lens formula to find the position of the image. The lens formula is given by:
1f=1v−1u
Where:
- f is the focal length (20 cm),
- u is the object distance (which is negative for real objects, so u=−25 cm),
- v is the image distance (which we need to find).
Substituting the known values into the lens formula:
120=1v−1−25
This simplifies to:
120=1v+125
To combine the fractions, we find a common denominator (100):
120=5100and125=4100
Thus, we have:
5100=1v+4100
Subtracting 4100 from both sides gives:
1100=1v
Taking the reciprocal of both sides, we find:
v=100 cm=1 m
Step 3: Determine the Linear Magnification
The linear magnification m of a lens is given by the formula:
m=hih=vu
Where:
- hi is the height of the image,
- h is the height of the object (1 cm),
- v is the image distance (100 cm),
- u is the object distance (-25 cm).
Substituting the known values:
m=100−25=−4
Step 4: Determine the Height of the Image
Using the magnification formula, we can find the height of the image:
m=hih
Rearranging gives:
hi=m⋅h
Substituting the values:
hi=−4⋅1 cm=−4 cm
Summary of Results
1. Focal length of the lens f=20 cm
2. Position of the image v=100 cm (1 m)
3. Linear magnification m=−4
4. Height of the image hi=−4 cm
The power P of a lens is related to its focal length f by the formula:
P=1f
Given that the power of the lens is 5D, we can rearrange the formula to find the focal length:
f=1P=15=0.2 m=20 cm
We will use the lens formula to find the position of the image. The lens formula is given by:
1f=1v−1u
Where:
- f is the focal length (20 cm),
- u is the object distance (which is negative for real objects, so u=−25 cm),
- v is the image distance (which we need to find).
120=1v−1−25
This simplifies to:
120=1v+125
To combine the fractions, we find a common denominator (100):
120=5100and125=4100
Thus, we have:
5100=1v+4100
Subtracting 4100 from both sides gives:
1100=1v
Taking the reciprocal of both sides, we find:
v=100 cm=1 m
The linear magnification m of a lens is given by the formula:
m=hih=vu
Where:
- hi is the height of the image,
- h is the height of the object (1 cm),
- v is the image distance (100 cm),
- u is the object distance (-25 cm).
m=100−25=−4
Using the magnification formula, we can find the height of the image:
m=hih
Rearranging gives:
hi=m⋅h
Substituting the values:
hi=−4⋅1 cm=−4 cm
1. Focal length of the lens f=20 cm
2. Position of the image v=100 cm (1 m)
3. Linear magnification m=−4
4. Height of the image hi=−4 cm
Topper's Solved these Questions
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-2
Explore 62 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Exercise-3
Explore 80 Videos
- GEOMATRICAL OPTICS Book:RESONANCE ENGLISHChapter:GEOMATRICAL OPTICS Exercise:Problem
Explore 33 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:HIGH LEVEL PROBLEMS
Explore 16 Videos
Similar Questions
Find the focal length and nature of a lens whose optical power is -5D.
View SolutionA thin linear object of size 1mm is kept along the principal axis of a convex lens of focal length 10cm. The object is at 15cm from the lens. The length of the image is:
View SolutionA convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?
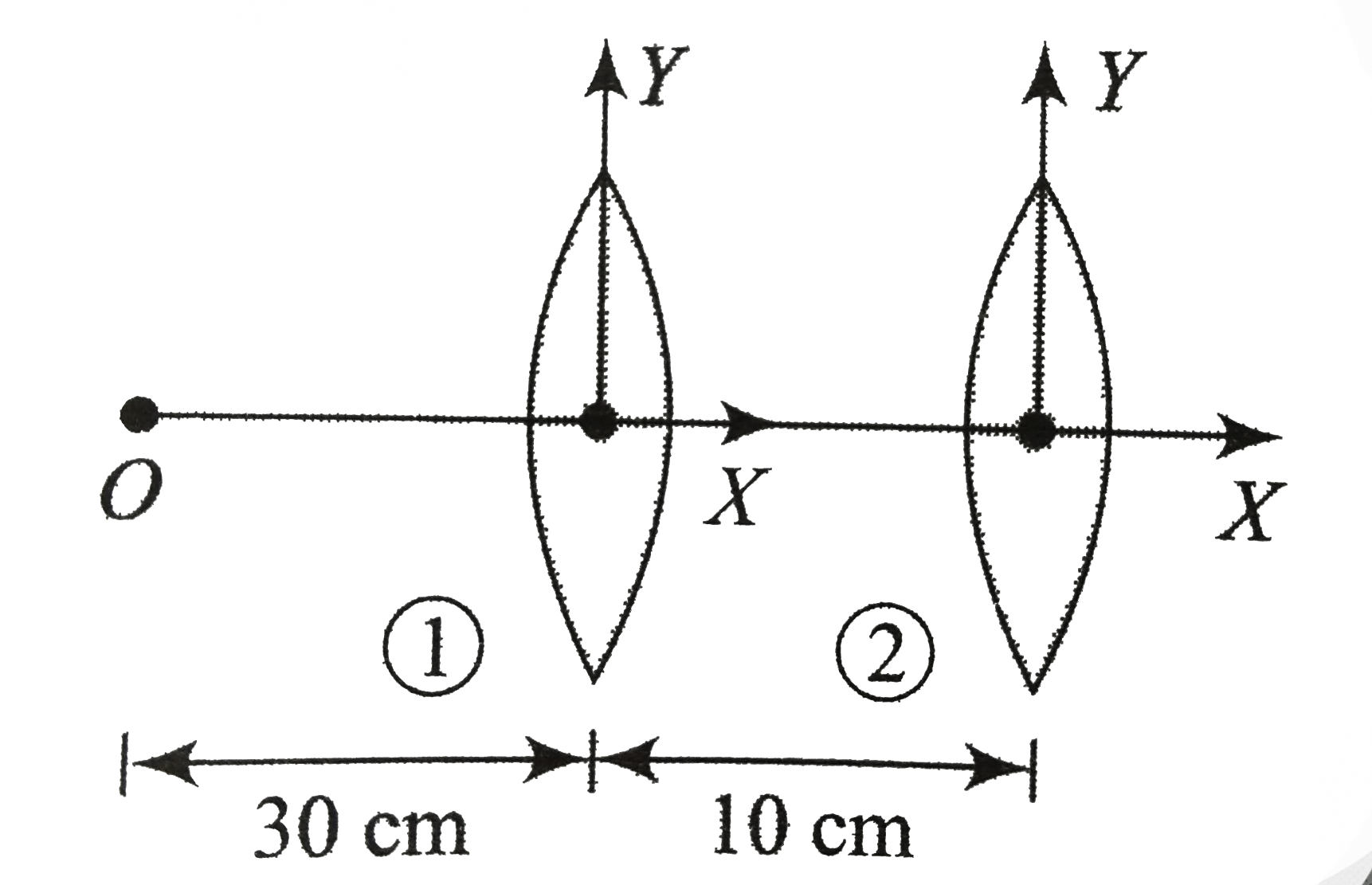
View SolutionA pin of length 1cm lies along the principle axis of a converging lens, the centre being at a distance of 5,5cm form the lens. The focal length of the lens is 3cm. Find the size of the image.
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View SolutionWhat is the optical power in dioptre of a concave lens of focal length 50 cm?
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionThe focal length of a converging lens is 8 cm. Fins the magnification power when it is used as a reading lens to form the image at near point.
View SolutionA 1.5 cm tall object is placed perpendicular to the principal axis of a convex lens of focal length 15 cm. Distance of object from the lens is 20 cm. Use lens formula to find the nature, position and size of the image.
View Solution(i) A diverging lens of focal length 15 cm, forms an image at distance of 10 cm from the lens. How far is the object placed from the lens ?
(ii) What is the linear magnification of the image?
View Solution

