Two identical thin converging lenses brought in contact so that their axes coincides are placed 12.5cm form an object. What is the optical power of the system and each lens, if the real image formed by the system of lenses if four times as large as the object?
The correct Answer is:10D, Optical pwer of each lens =5D
To solve the problem step by step, we will follow the given information and apply the relevant formulas.
Step 1: Understand the given data
- Distance of the object (U) = -12.5 cm (the negative sign indicates that the object is on the same side as the incoming light).
- Magnification (M) = 4 (the image is four times larger than the object).
- Since the image is real, the magnification is given by the formula:
M=VU
where V is the image distance.
Step 2: Calculate the image distance (V)
Using the magnification formula:
M=VU
Substituting the values:
4=V−12.5
Rearranging gives:
V=4×(−12.5)=−50 cm
Step 3: Use the lens formula to find the focal length (F)
The lens formula is given by:
1F=1V−1U
Substituting the values of U and V:
1F=1−50−1−12.5
Calculating the right side:
1F=−150+112.5
Finding a common denominator (50):
1F=−150+450=350
Thus:
F=503 cm≈16.67 cm
Step 4: Calculate the optical power of the system
The optical power (P) is given by:
P=1F
Where F must be in meters:
F=503 cm=50300 m=16 m
Thus:
P=116=6 diopters
Step 5: Calculate the power of each lens
Since the two lenses are identical and in contact, the total power of the system is the sum of the powers of the individual lenses:
Ptotal=P1+P2
Since P1=P2=P0:
Ptotal=2P0
Thus:
6=2P0
So:
P0=3 diopters
Summary of Results
- The optical power of the system is 6 diopters.
- The power of each lens is 3 diopters.
- Distance of the object (U) = -12.5 cm (the negative sign indicates that the object is on the same side as the incoming light).
- Magnification (M) = 4 (the image is four times larger than the object).
- Since the image is real, the magnification is given by the formula:
M=VU
where V is the image distance.
Using the magnification formula:
M=VU
Substituting the values:
4=V−12.5
V=4×(−12.5)=−50 cm
The lens formula is given by:
1F=1V−1U
1F=1−50−1−12.5
1F=−150+112.5
1F=−150+450=350
F=503 cm≈16.67 cm
The optical power (P) is given by:
P=1F
Where F must be in meters:
F=503 cm=50300 m=16 m
P=116=6 diopters
Since the two lenses are identical and in contact, the total power of the system is the sum of the powers of the individual lenses:
Ptotal=P1+P2
Since P1=P2=P0:
Ptotal=2P0
Thus:
6=2P0
So:
P0=3 diopters
- The optical power of the system is 6 diopters.
- The power of each lens is 3 diopters.
Topper's Solved these Questions
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-2
62 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Exercise-3
80 Videos
- GEOMATRICAL OPTICS BOOK - RESONANCE ENGLISHCHAPTER - GEOMATRICAL OPTICS EXERCISE - Problem
33 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS
16 Videos
Similar Questions
An object 15cm high is placed 10cm from the optical center of a thin lens. Its image is formed 25cm from the optical center on the same side of the lens as the object
View SolutionAn illuminated object is placed on the principal axis of a converging lens so that real image is formed on the other side of the lens. If the object is shifted a little,
View SolutionTwo thin lenses, both of 10 cm focal length- one convex and other concave, are placed 5 cm apart. An object is placed 20 cm in front of the convex lens. Find the nature and position of the final image.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionTwo thin converging lenses are placed on a common axis, so that the centre of one of them coincides with the focus of the other. An object is placed at a distance twice the focal length from the left hand lens. Where will its image be? What is the lateral magnification? The focal of each lens is f.
View SolutionWhat should be the value of distance d so that final image is formed on the object itself. (Focal length of the lenses are written on the lenses.)
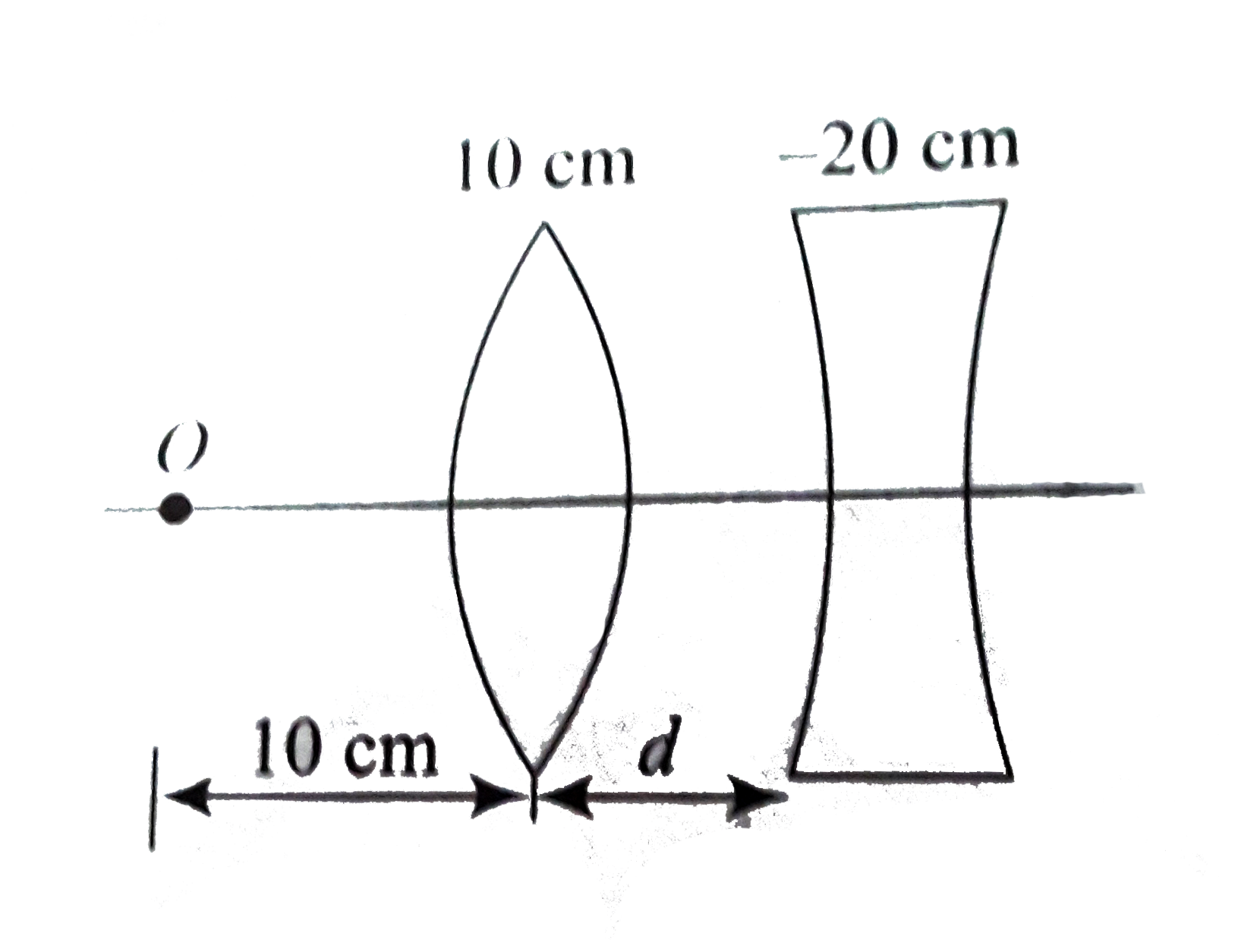
View SolutionA thin equiconvex glass lens (μ1=1.5) of radius of curvature 'R' and a thin plano-concave lens (μ2=1.4) are kept in contact and the plane surface is silvered. This lens system is placed in air. When a point object is placed at a distance 20cm from the lens system on its principal axis, the image formed by the lens system coincides with the object. Then the value of radius of curvature 'R' is

View SolutionA convex lens of focal length 30 cm produces 5 times magnified real image of an object. What is the object distance?
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View Solution
