A particle of mass 0.50 kg executes a simple harmonic motion under a force F=−(50Nm−1)x. If it crosses the centre of oscillation with a speed of 10ms−1, find the amplitude of the motion.
The kinetic energy of the particle when it is the centre of oscillation is
E=12mv2,=12(0.50kg)(10m/s)2,=25J.
The potential energy is zero here. At the maximum displacement x=A, the speed is zero and hence the kinetic enery is zero. The potential energy here is 12kA2. As there is no loss of energy.
12kA2=25J.......(i)
The force on the particle is given by
F=−(50N/m)x.
Thus, the spring constant is k=50N/m
Equation (i) gives
12(50N/m)A2=25J or, A=1m
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems9videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise24videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
Similar Questions
A particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle executes simple harmonic motion of period 16s. Two seconds later after it passes through the center of oscillation its velocity is found to be 2m/s. Find the amplitude.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA partical of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assum at t=0. The partical start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
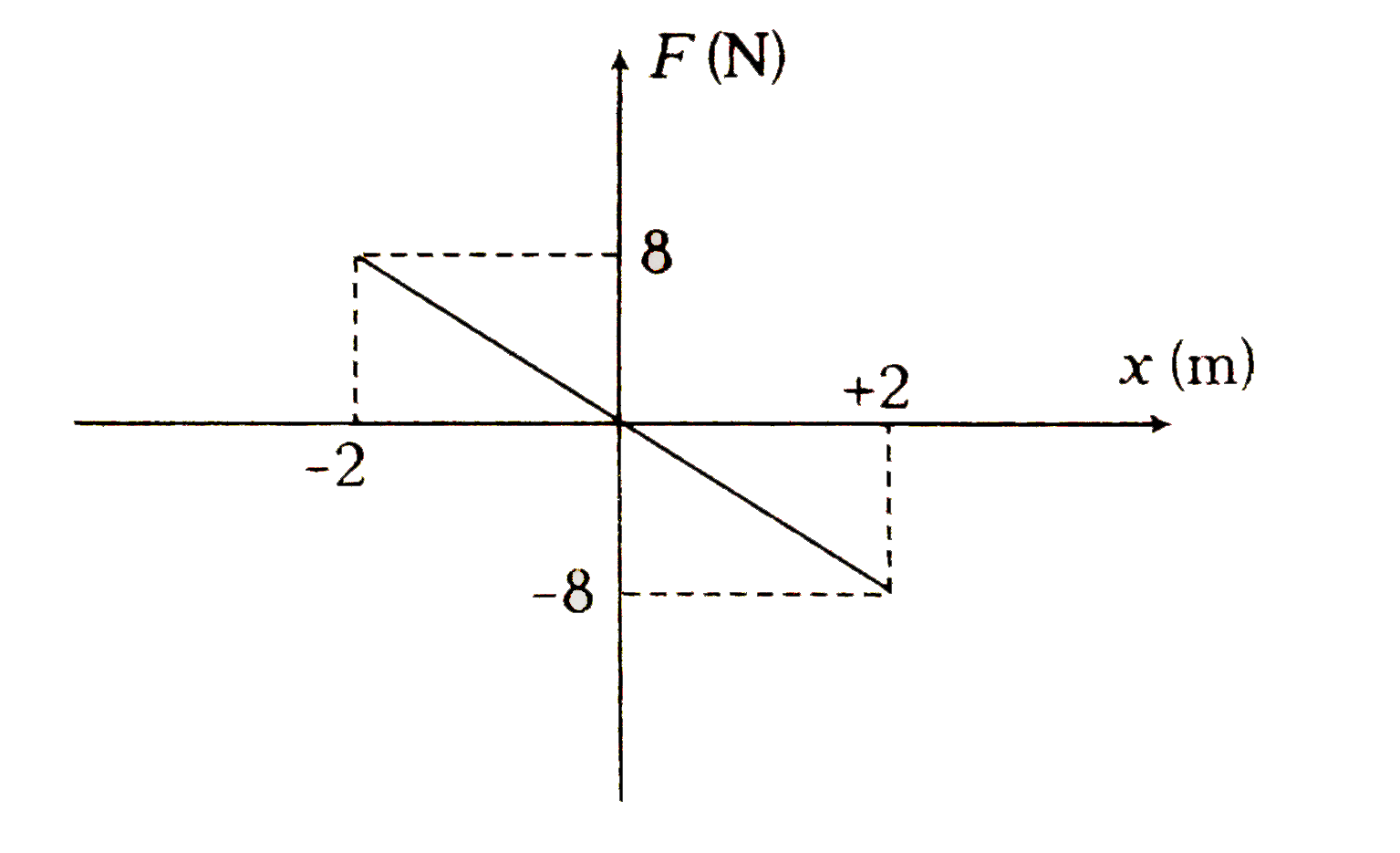 View Solution
View SolutionA body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
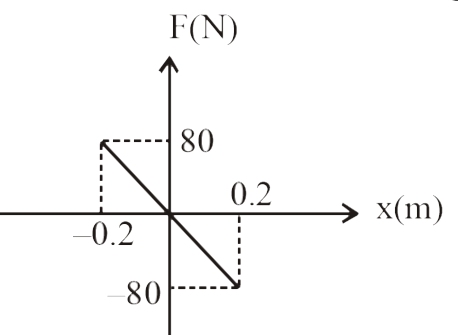 View Solution
View SolutionA particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cm / s . The frequency of its oscillation is
View Solution
