A piston of diameter and long works in a cylinder of diameter as shown in figure. If the annular space is filled with a lubricating oil of viscosity centipoises, calculate the constant speed (nearest to integer) of descent of piston in vertical position. The weight of piston and the axial load are .

The correct Answer is:
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - III
Explore 8 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 3 PART - I
Explore 7 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - I
Explore 9 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 92 illustration
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 43 Videos
Similar Questions
A syringe of diameter D = 8 mm and having a nozzie of diameter d = 2 mm is placed horizontally at a height of 1.25 m as shown in the figure . An incompressible and non - viscous liquid is filled in syringe and the piston is moved at speed of 0.25 m/s .Find the range of liquid jet on the ground.

View Solution(i) A conducting cylinder whose inside diameter is 4.00cm contains air compressed by a piston of mass m=13.0kg, which can slides freely in the cylinder shown in the figure. The entire arrangement is immersed in a water bath whose temperature can be controlled. The syetem is initially in equilibrium at temperature t1=20∘C. The initial height of the piston above the bottom of the cylinder is hi=4.00cm.Patm=1×105Nm2 and g=10m/s2.
If the temperature of the water bath is gradually increased to a final temperature tf=100∘C. Find teh height hf of the piston (in cm) at that instant?
(ii) In the above question, if we again start from the initial conditions and the temperature is again gradually raised, and weights are added to the piston to keep its height fixed at hi. Find the value of teh added mass when the final temperature becomes tf=100∘C?

View Solution2.00 mole of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston. The piston is connected to a vertical spring of spring constant 200Nm−1 as shown in .the area of cross section of the cylinder is 20.0cm2. initially, the spring is at its natural length and the temperature of the gas is 300K at its natural length. the atmosphere pressure is 100 kPa. the gas is heated slowly for some time by means of an electric heater so as to move the position up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.

View SolutionA steel wire of diameter 0.8 mm and length 1m is clamped firmly at two points P and Q which are one metre apart and in the same horizontal plane. A body is hung from the middle point of the wire, such that the middle point sags one cm lower from the original position as shown in figure. Calculate the mass of the body. Y=2×1011N/m2.
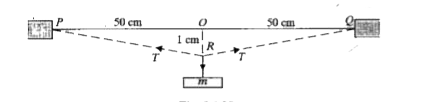
View SolutionA long cylindrical tank of cross-sectional area 0.5m2 is filled with water. It has a small hole at a height 50cm from the bottom. A movable piston of cross-sectional area almost equal to 0.5m2 is fitted on the top of the tank such that it can slide in the tank freely. A load of 20kg is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is 1m above the bottom. (Ignore the mass of the piston)

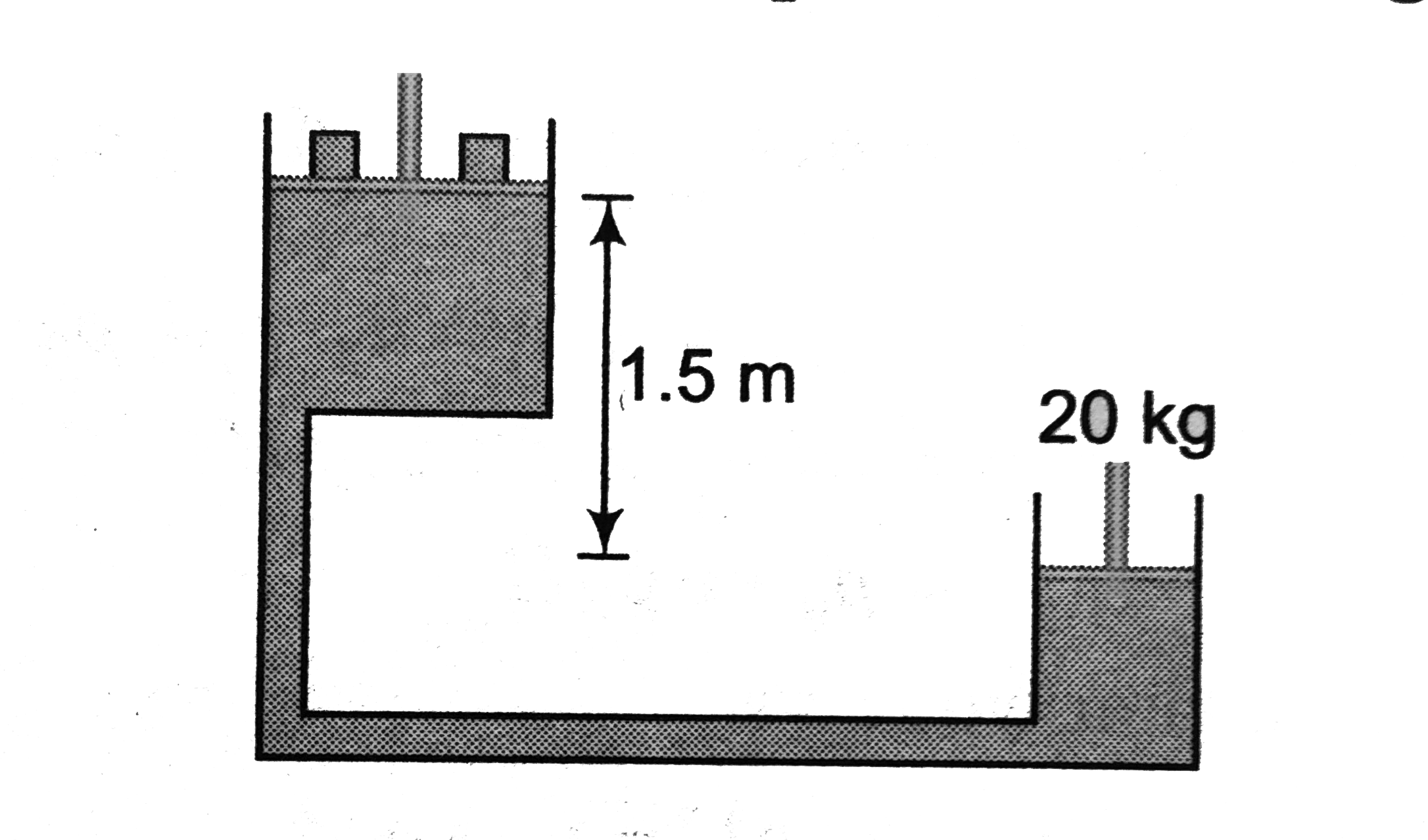
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
View Solution

