Two moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
The correct Answer is:K=2000N/m,Q=923 Joules approx.
To solve the problem, we will follow these steps:
Step 1: Calculate the heat supplied by the heater (Q)
The heat absorbed by the system can be calculated using the formula:
Q=nCpΔT
Where:
- n=2 moles (given)
- Cp for a monoatomic gas is 52R
- R=8.314J/(mol⋅K)
- ΔT=50K
Substituting the values:
Cp=52×8.314=20.785J/(mol⋅K)
Q=2×20.785×50=2078.5J
Step 2: Calculate the change in internal energy (U)
The change in internal energy can be calculated using the formula:
U=nCvΔT
Where:
- Cv for a monoatomic gas is 32R
Substituting the values:
Cv=32×8.314=12.471J/(mol⋅K)
U=2×12.471×50=1247.1J
Step 3: Apply the first law of thermodynamics
According to the first law of thermodynamics:
Q=U+W
We can rearrange this to find W:
W=Q−U
Substituting the values:
W=2078.5−1247.1=831.4J
Step 4: Determine the work done on the spring
The total work done (W) is the sum of the work done by the gas and the work done on the spring:
W=Wgas+Wspring
Where:
- Wgas=50J (given)
Thus:
Wspring=W−Wgas=831.4−50=781.4J
Step 5: Relate the work done on the spring to the spring constant (k)
The work done on the spring can be expressed as:
Wspring=12kx2
Where:
- x=0.1m (displacement)
Substituting the values:
781.4=12k(0.1)2
781.4=12k(0.01)
k=781.4×20.01=15628N/m
Final Answers:
- The spring constant k is 15628N/m.
- The heat supplied by the heater Q is 2078.5J.
---
Q=nCpΔT
- n=2 moles (given)
- Cp for a monoatomic gas is 52R
- R=8.314J/(mol⋅K)
- ΔT=50K
Cp=52×8.314=20.785J/(mol⋅K)
Q=2×20.785×50=2078.5J
U=nCvΔT
- Cv for a monoatomic gas is 32R
Cv=32×8.314=12.471J/(mol⋅K)
U=2×12.471×50=1247.1J
Q=U+W
W=Q−U
Substituting the values:
W=2078.5−1247.1=831.4J
W=Wgas+Wspring
Where:
- Wgas=50J (given)
Wspring=W−Wgas=831.4−50=781.4J
Wspring=12kx2
- x=0.1m (displacement)
781.4=12k(0.1)2
781.4=12k(0.01)
k=781.4×20.01=15628N/m
- The spring constant k is 15628N/m.
- The heat supplied by the heater Q is 2078.5J.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Advancel Level Problems
Explore 1 Video
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
3 moles of an ideal gas are contained within a cylinder by a frictionless piston and are initially at temperature T . The pressure of the gas remains constant while it is heated and its volume doubles . If R is molar gas constant , the work done by the gas in increasing its volume is
View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T1, pressure P1 and volume V1and the spring is in its relaxed state. The gas is then heated very slowly to temperature T2,pressure P2and volume V2. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View SolutionTwo moles of an ideal gas is contained in a cylinder fitted with a frictionless movable piston, exposed to the atmosphere, at an initial temperature T0. The gas is slowly heated so that its volume becomes four times the initial value. The work done by gas is
View SolutionTwo moles of an ideal monoatomic gas are contained in a vertical cylinder of cross sectional area A as shown in the figure. The piston is frictionless and has a mass m. At a certain instant a heater starts supplying heat to the gas at a constant rate qJ/s. Find the steady velocity of the piston under isobaric condition. All the boundaries are thermally insulated.

View Solution2 moles of a diatomic gas are enclosed in a cylinder piston arrangment. The area of cross section and mass of the piston are 1cm2 and 1 kg respectively. A heater is supplying heat to the gas very slowly. Find heat supplied (in joule) by the heater is the piston moves through a distance of 10 cm.
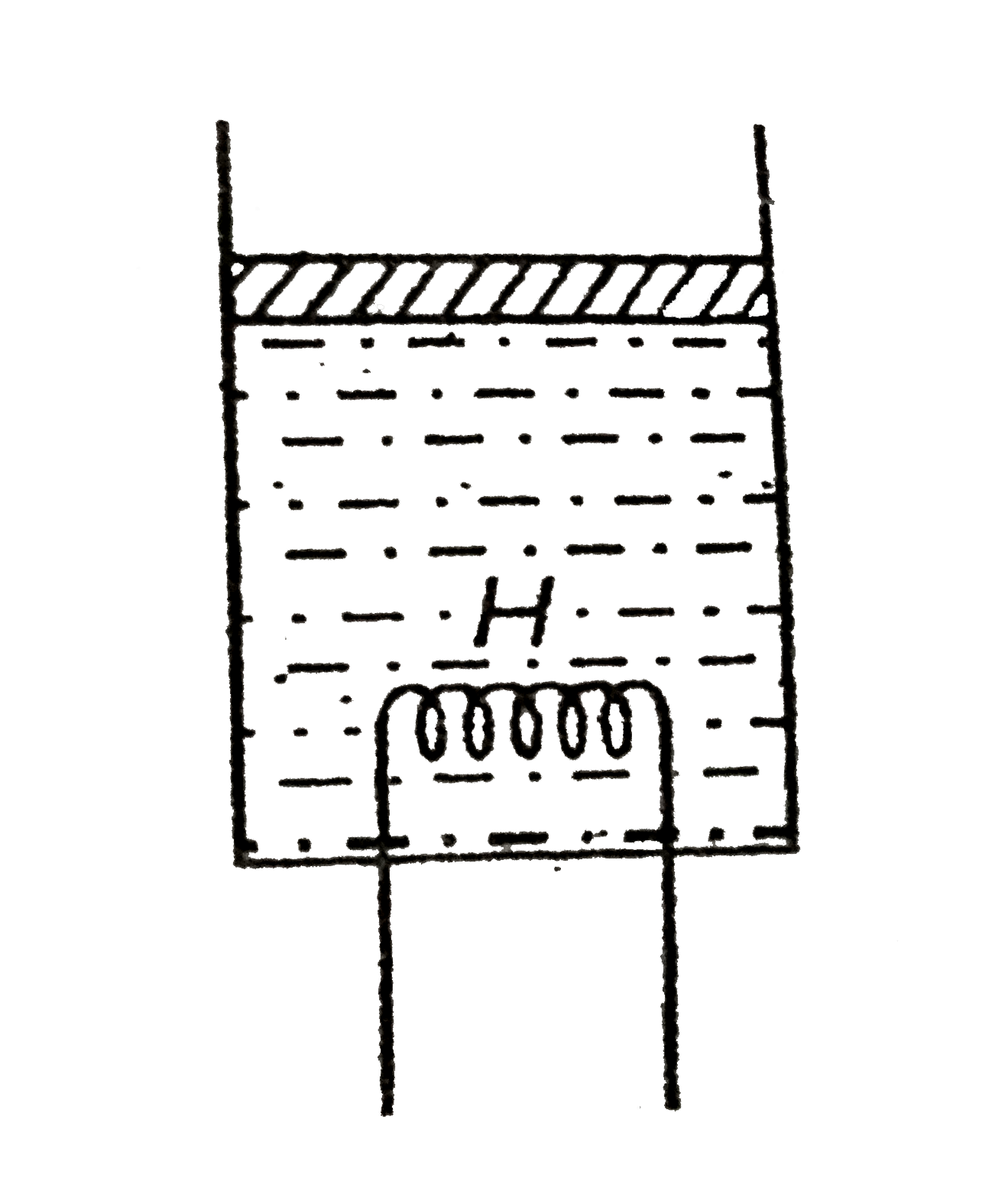 .
.
View SolutionTwo moles of an ideal gas are contained in a vertical cylinder with a frictionless piston. The piston is slowly displaced so that expansionin gas is isothermal at temperature T0=400K. find the amount of work done in increasing the volume to 3 times.t ake atmospheric pressure =105N/m2
View SolutionAn ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10cm2and weight 1kg. The length of the gas column in the vessel now taken into a spaceship revolving round the earth as satellite. The air pressure in the spaceship is maintained at 100kPa. Find the length of the gas column in the cylinder.
View SolutionAn ideal gas has a volume 0.3m3 at 150kPa. It is confined by a spring-loaded piston in a vertical cylinder. Initially, the spring is in relaxed state. If the gas is heated to a final state of 0.5m3 and pressure 600kPa find the work done on the spring (atmospheric pressure, P0=1×105N/m2).

View Solution

