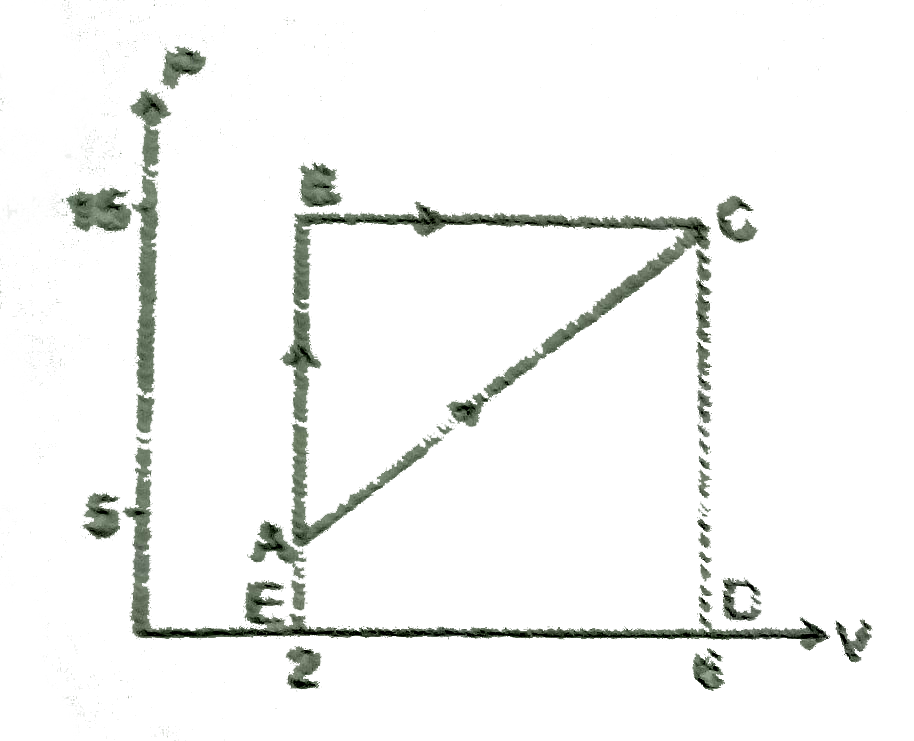
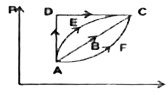
In the given figure, an ideal gas changes it state from A to state C by two paths ABC and AC.
(i) Find the path along which work done is the least.
(ii) The internal energy of the gas at A to 10J and the amount of heat supplied to change its state to C through the path AC is 200J. Calculate the internal energy at C.
(iii) The internal energy of the gas at state B is 30J. Find the amount of heat supplied to the gas to go from A→B.

The correct Answer is:(i) along AC
(ii) 170J (iii) 20J
(i) Along path AC work done is least. As areas under P−V diagram along AC is less as compare to along path ABC
ΔWABC=Area under the EABCDE=15×4=60J.
ΔWAC= Area under EACDE=5×4+10×42=40J.
(ii) ΔWAC=40J (as calculated above)
ΔQAC=200J.
∴ΔUAC=ΔQAC−ΔWAC=200−40=160
UAC=UC−UA=160
∴UC=UA+160=10+160=170J,
(iii) ΔWAB=0
Ideal gas equation PV=nRT
ΔP.V=nRΔT(∵V=const)
ΔT=ΔP.VnR
ΔU=nCvΔT=nCv.ΔPVnR=−CvR.ΔP.V
∴UB=CVRPB.V
UA=CVRPA.V
Given UB=30
CVR×PB×V=CVR×15×2
=30×CVR=30,CVR=1
∴UA=CVR=30,CVR=1
∴UA=CVR×PA×V=1×5×2=10J
∴ΔUAB=UB−UA=30−10=20J
∴ΔQA→B=ΔUA→B+ΔWA→B=20+0=20J.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Advancel Level Problems
1 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
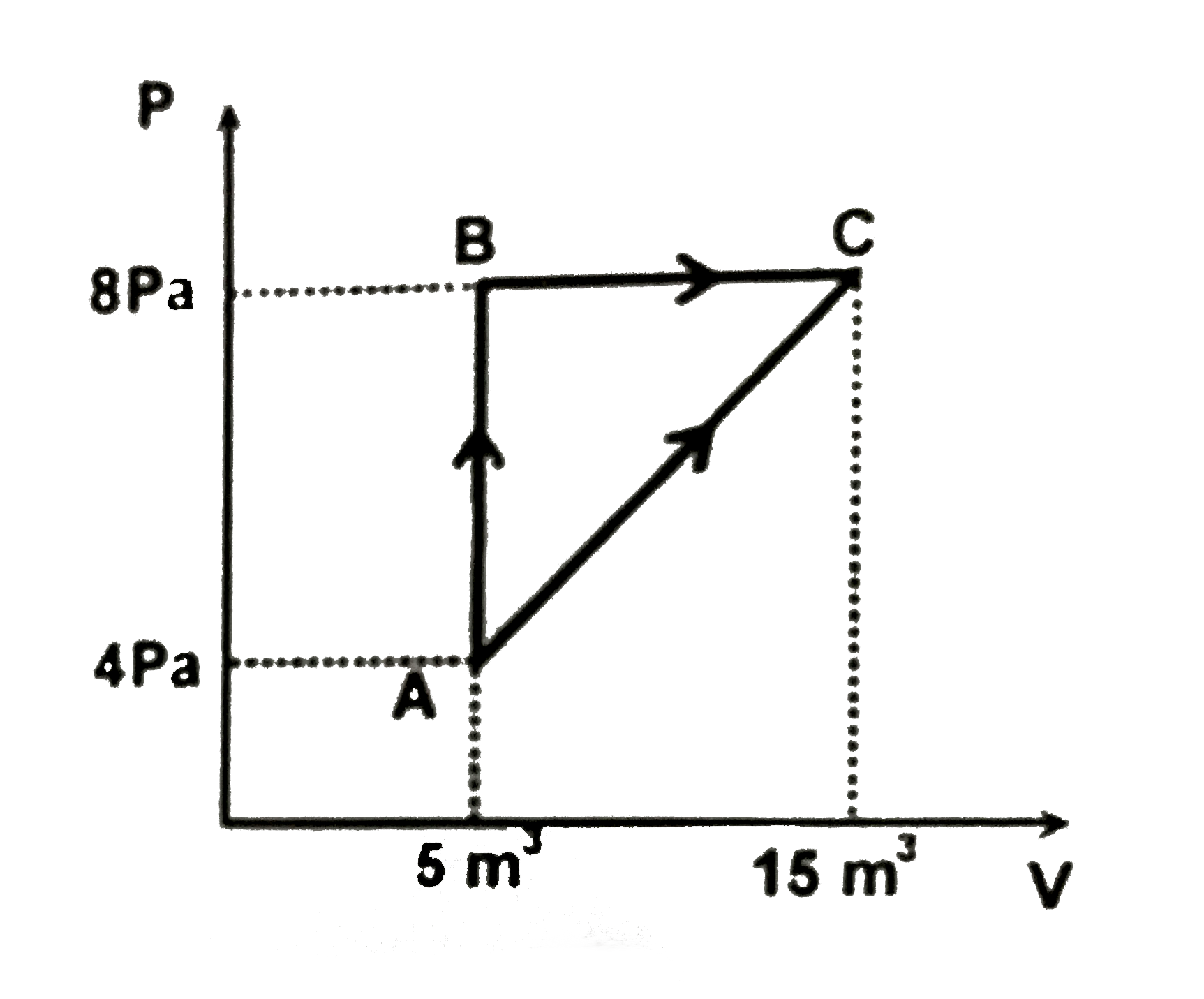
In the given figure an ideal gas changes its state from A to state C by two paths ABC and AC.
_E01_269_Q01.png)
(i) Find the path along which work done is the least.
(ii) The internal energy of gas at A and B is 10J and 20 J respectively amount of heat supplied to change its state to C through the path AC is 200J. Calculate the internal energy at C.
(iii) How much is the heat involved in the process ABC and ADC?
View SolutionIn the given figure, an ideal gas changes its state from A to state C by two paths ABC and AC.
_E01_269_Q01.png)
Along which path the work done by the gas is least.
View SolutionIn the given graph, an ideal gas changes its state from A to C by two paths ABC and AC.
(a) Find the path along which work done is less.
(b) The internal energy of gas at A is 10J and the amount of heat supplied in path AC is 200J. Calculate the internal energy of gas at C.
(c) The internal energy of gas at state B is 20J. Find the amount of heat supplied to the gas to go from A to B.
View SolutionIn the given an ideal gas can change its state from A to C by two paths ABC or AC. Then
View SolutionThe relationship between enthalpy and internal energy change is
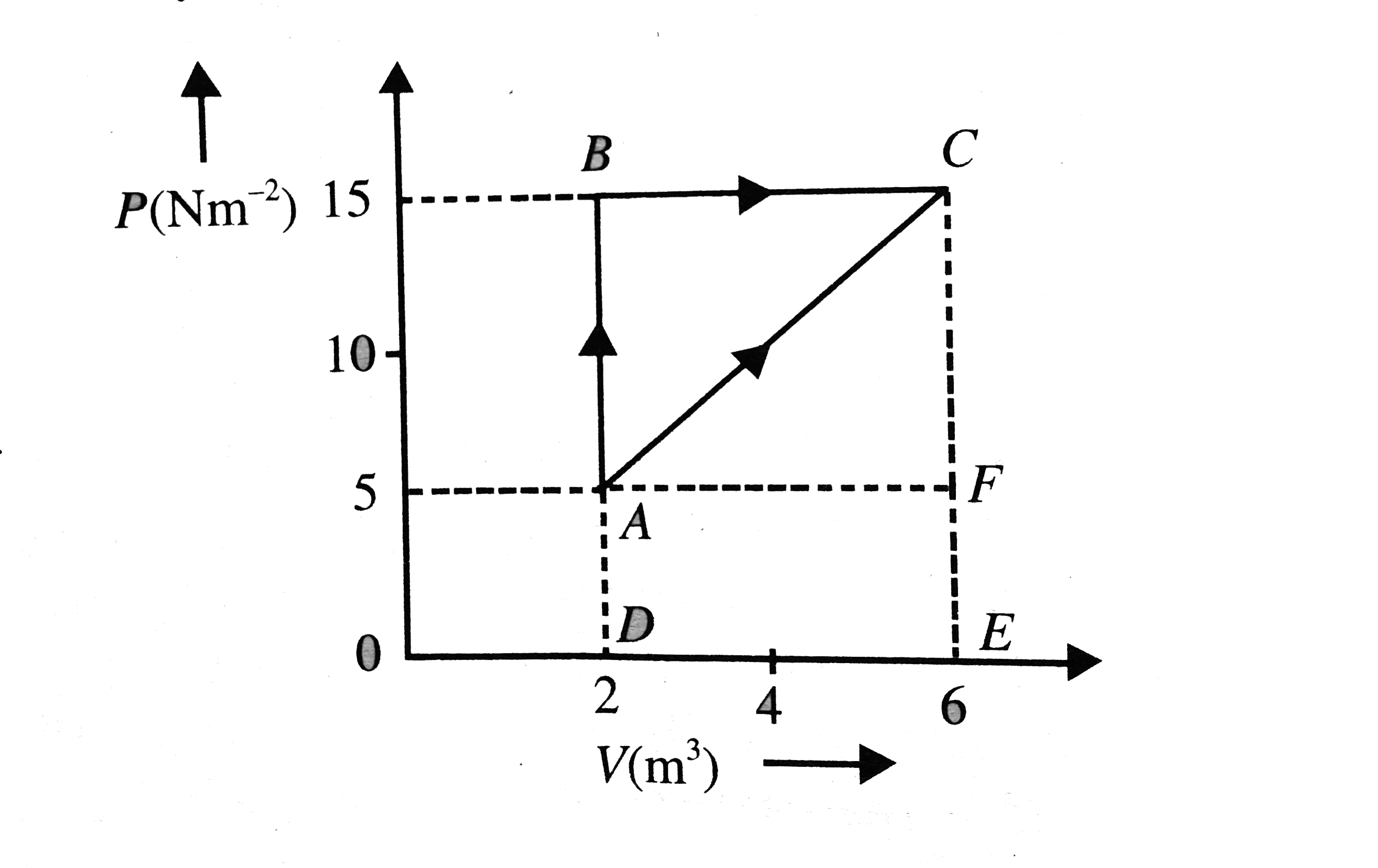
View SolutionThe given figure shown a change of state A to state C by two paths ABC and AC for an ideal gas. Calculate the :
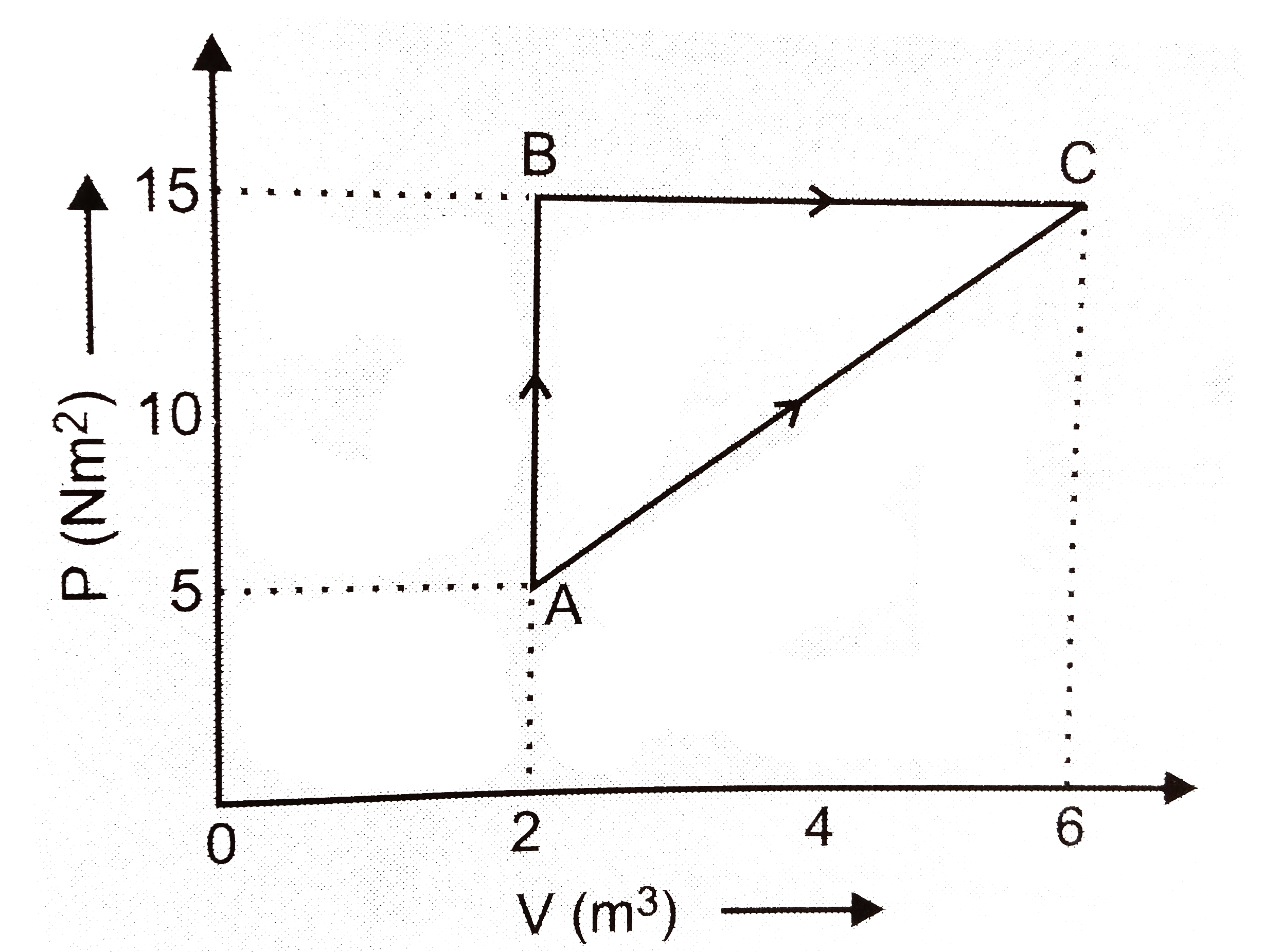
(a) Path along which work done is least.
(b) Internal energy at C if the internal energy of gas at A is 10J and amount of heat supplied to change its state to C through the path AC is 200J.
(c) Amount of heat supplied ot the gas to go from A to B, if internal energy of gas at state B is 10J.
View SolutionFigure shows an ideal gas changing its state A to state C by two different path ABC and AC. The internal energy of the gas at A is 10J and the amount of heat supplied to change its state to C through the path AC is 200J. Find the internal energy at C.
View SolutionIn the given figure, an ideal gas changes its state from state state C by two paths ABC and AC.
_E01_269_Q01.png)
How much is the heat involved in the process ABC and ADC ? The internal energy of gas at A and B is 10 J and 20 J respectively
View SolutionIn the given figure, an ideal gas changes its state from state state C by two paths ABC and AC.
_E01_269_Q01.png)
The internal energy of gas at A is 10 J and the amount of heat supplied to change its state to C through path AC is 200 J.Calculate the internal energy of gas at C
View SolutionIn the given figure, an ideal gas changes its state from A to C by four paths. The path for which work done is least, is
View Solution
