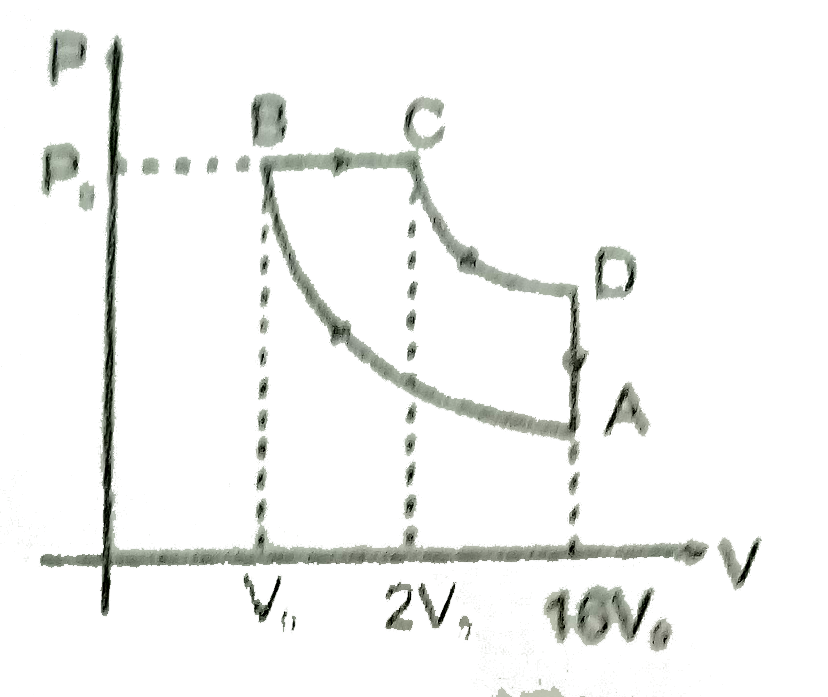
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression. B→C is isobaric expansion, D→A an adiabatic expansion and is isochoric.
The volume ratio are VA/VB−16 and VC/VB−2 and the temperature at TA=300k is
Find the temperature of the gas at the point (in K).
The correct Answer is:TB=600×23/5K,
TD=1200×2−3/5K,η=61.37%
The corresponding P−V diagram is as shown
Given : TA=300K,n=1,γ=1.4,VA/VB=16
andVC/VB=2LetVB=V0andPB=P0ThenVC=2V0andVA=16V0TemperatureatBB
Process A−B is adiabatic. Hence
TAVγ−1A=TBVγ−1B
or TB=TA(VAVB)γ−1
=(300)(16)1.4−1
=600×23/5K,
Temperature at D
B→C is an isobaric process (P= constant)
∴T∝V
VC=2VB
∴TC=2TB=(2)600×23/5K
TC=1200×23/5K
Now the process C−D is adiabatic.
Therefore
∴TD=TC(VCVD)γ−1=1200×23/5(216)1.4−1
TD=1200×23/5K,
Efficiency of cycle-
Efficiency of cycle (in percentage) is defined as
η=Net work doen in the cycleHeta absorbed in the cycle×100
η=WTotalQ+ve×100
=Q+ve=−Q−veQ+ve×100=(1−Q1Q2)×100...(1)
where Q1= Negative heat in the cycle (heat released)
and Q2= Positive heat in the cycle (heat absorbed) In the cycle-
QAB=QCD=0 (Adiabatic process)
In process DA:ΔQ=ΔU+ΔW(ΔW=0)
QDA=nCvΔT=(1)(52R)(TA−TD)(Cv=52R for a diatomic gas)
=52×8.31(300−791.7)J
[TD=1200×23/5K=791.K]
or QDA=−10215.06J (Release)
and QBC=nCPΔT=(1)(72R)(TC−TB)(CP=72R for a diatomic gas)
=(72)(8.31)(181.8−909.4)J
[TD=1200×23/5K≈1818.8K,TB=600×23/5≈909.4K]
or QBC=26449.89J
Therefore, substituting Q1=10215.06J and Q2=26449.89J in diatomic (1) we get-
∴η={1−10215.0626449.89}×100
or η=61.37%
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Advancel Level Problems
Explore 1 Video
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionAn ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state

View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
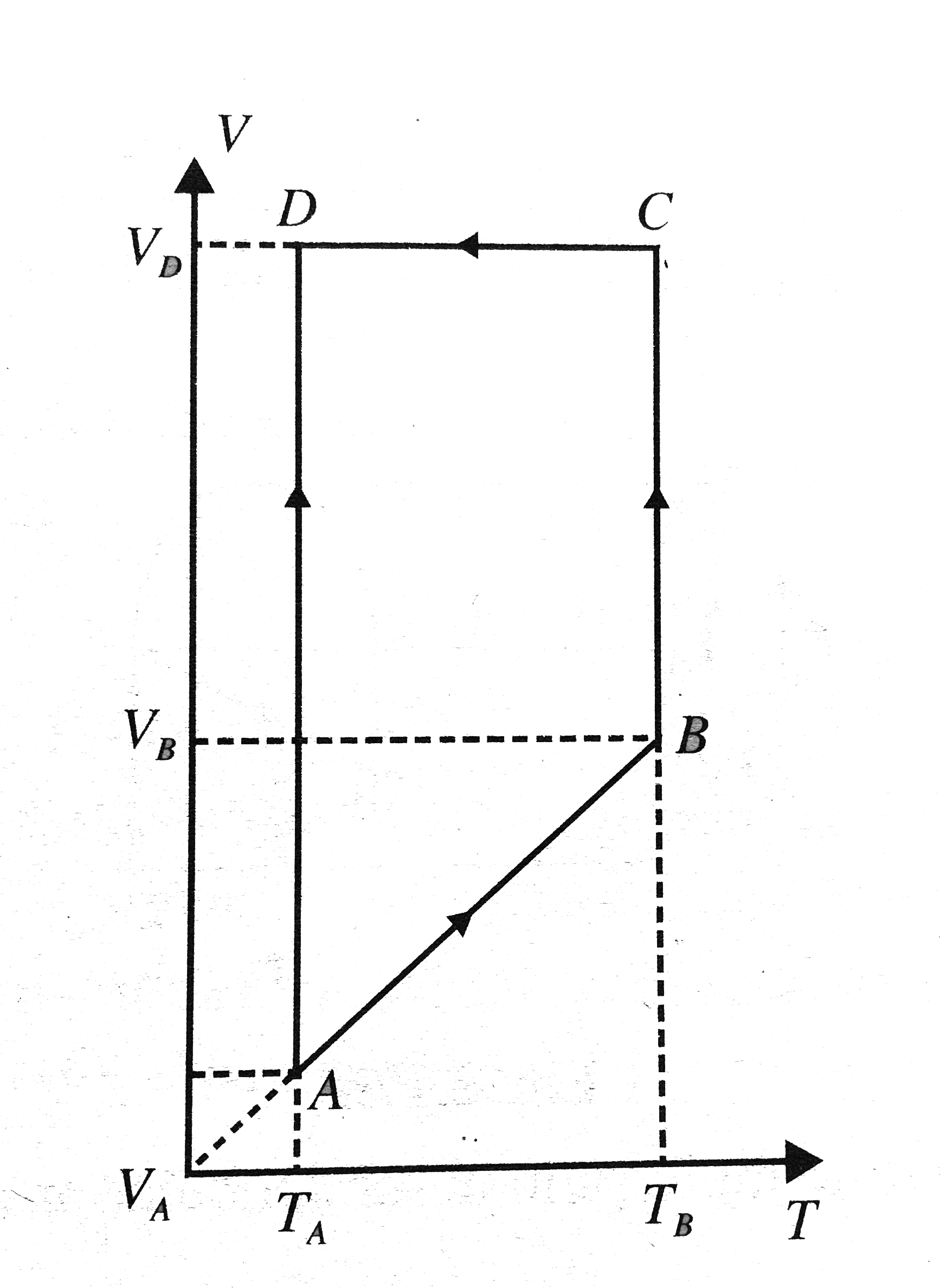
The temperature of the gas at point B
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate the temperature of the gas at point B
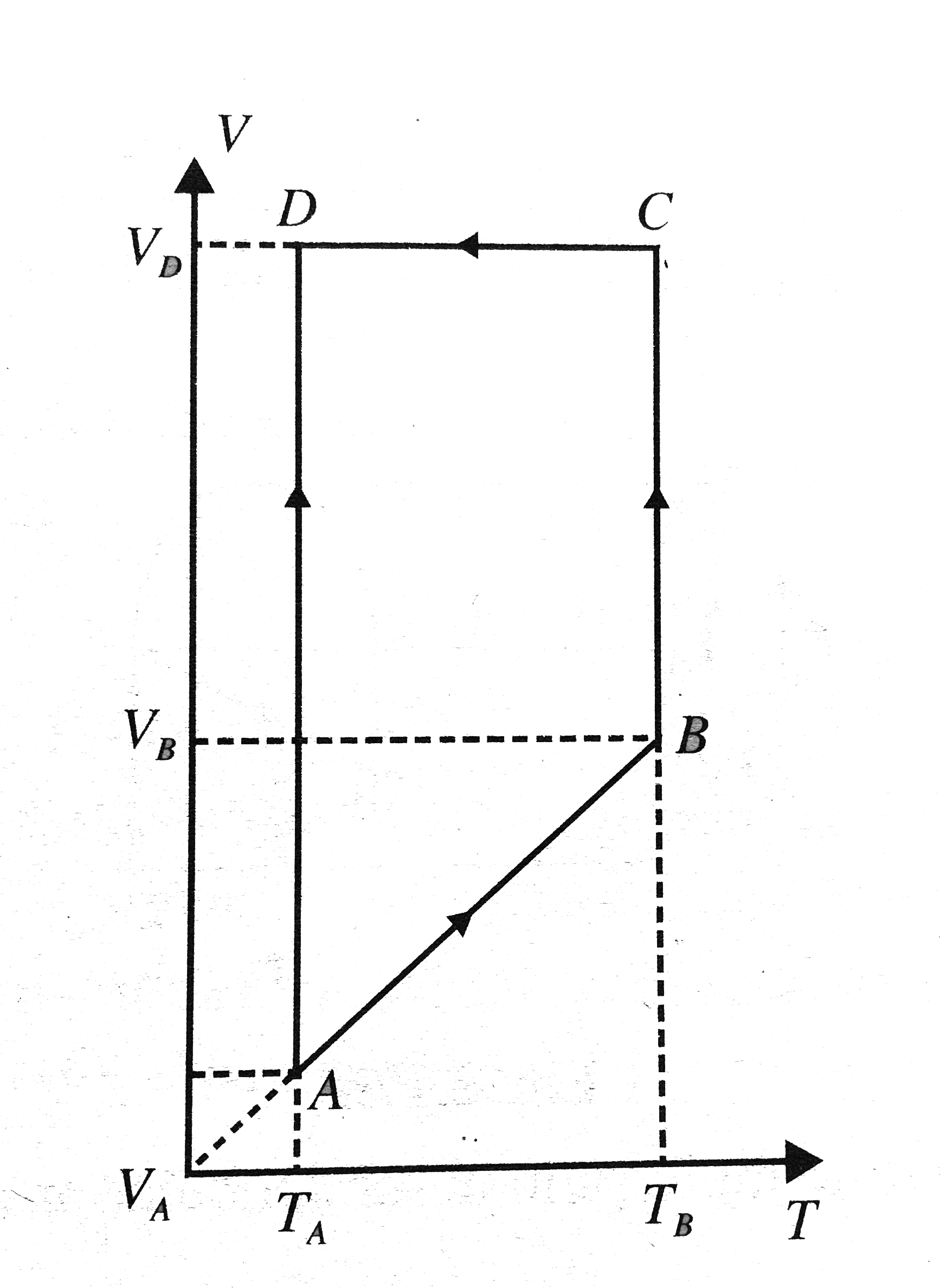
View SolutionA monoatomic ideal gas of two mole is taken through a cyclic process starting from A as shown VB/VA=2andVD/VA=4 Temperature TAis27∘C
The work done during the process D→A is
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
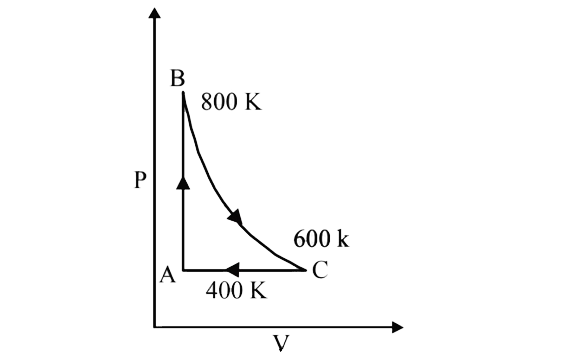
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:

View Solution
A monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown
VBVA=2 and VDVA=4
Temperature TA at A is 27∘C.
Q. Temperature at C is
View SolutionIn adiabatic process, the work involved during expansion or compression of an ideal gas is given by :
View Solution

