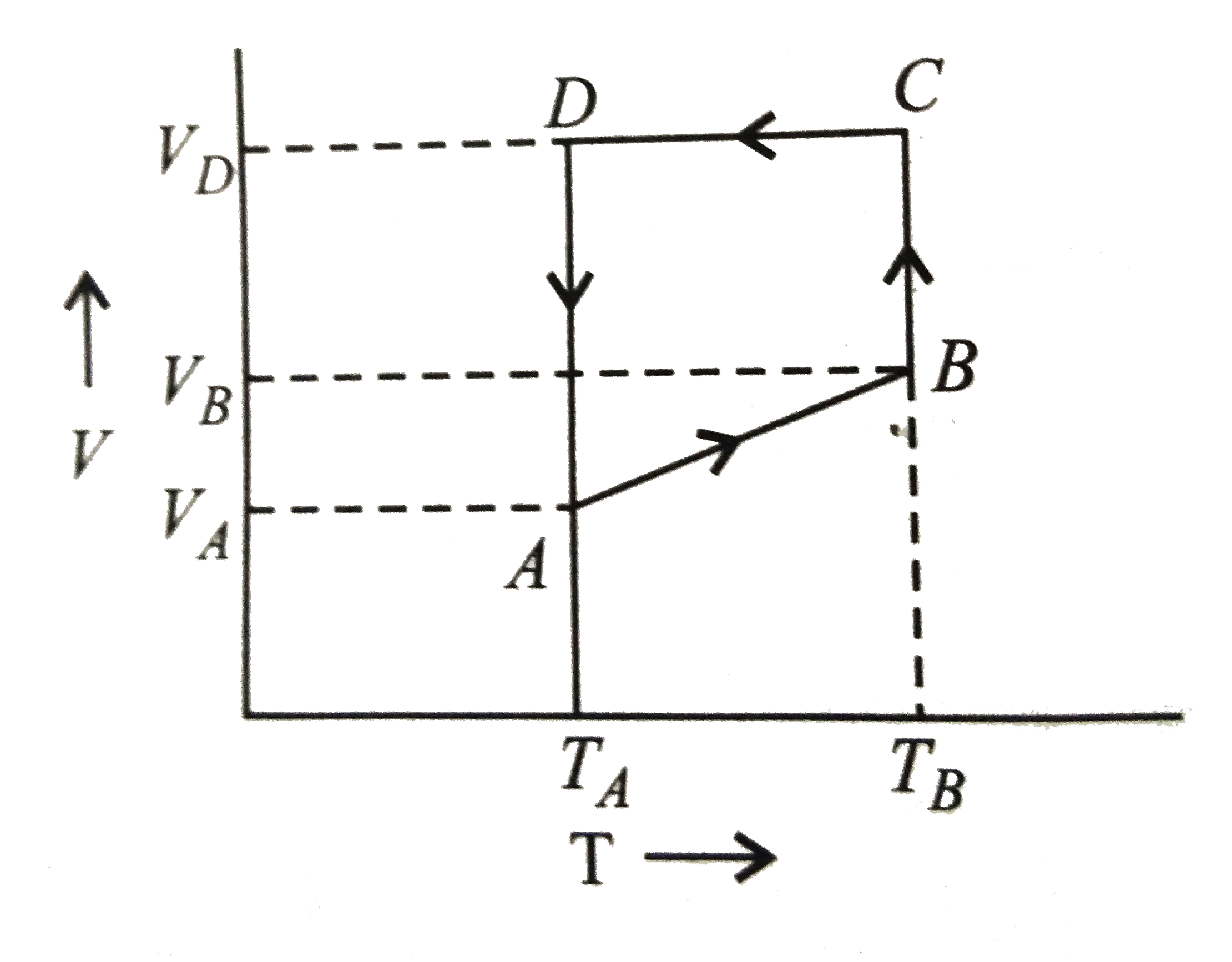
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
The correct Answer is:909
To solve the problem step by step, we will calculate the temperatures at points B and D, and then find the efficiency of the cycle.
Step 1: Calculate Temperature at Point B (T_B)
1. Identify the process from A to B: This is an adiabatic compression process.
2. Use the adiabatic relation: For an adiabatic process, we have the relation:
TBTA=(VAVB)γ−1
where γ=1.4 for a diatomic ideal gas.
3. Substitute the known values:
- TA=300K
- VAVB=16
Therefore,
TB=TA(VAVB)γ−1=300(16)0.4
4. Calculate TB:
TB=300×160.4≈300×2.297≈689.1K
Step 2: Calculate Temperature at Point D (T_D)
1. Identify the process from C to D: This is also an adiabatic process.
2. Use the adiabatic relation:
TDTC=(VCVD)γ−1
Since VD=VA (isochoric process from D to A), we need to find VC first.
3. Calculate VC:
- Given VCVB=2, we can express VC in terms of VB:
VC=2VB
4. Calculate VD:
- Since VD=VA and VAVB=16:
VD=16VB
5. Now substitute into the equation:
VCVD=2VB16VB=18
6. Use the relation to find TD:
TD=TC(VCVD)γ−1=TC(18)0.4
7. Calculate TC:
- From the isobaric process B to C:
TCTB=VCVB⇒TC=TB⋅VCVB=689.1⋅2≈1378.2K
8. Now substitute TC into the equation for TD:
TD=1378.2(18)0.4≈1378.2⋅0.5≈689.1K
Step 3: Calculate Efficiency of the Cycle
1. Identify the heat supplied (Q_s): The heat supplied occurs during the isobaric process (B to C):
Qs=nCP(TC−TB)
where CP=Rγγ−1.
2. Calculate CP:
CP=R⋅1.40.4=3.5R
3. Substitute values into Qs:
Qs=1⋅3.5R⋅(1378.2−689.1)≈3.5R⋅689.1
4. Calculate work done (W_net): The net work done is the sum of work done in all processes:
Wnet=Qs−Qr
where Qr is the heat rejected during the isochoric process (D to A).
5. Calculate efficiency:
η=WnetQs⋅100
Final Results
- Temperature at B: TB≈689.1K
- Temperature at D: TD≈791K
- Efficiency of the cycle: η≈61.4%
2. Use the adiabatic relation: For an adiabatic process, we have the relation:
TBTA=(VAVB)γ−1
where γ=1.4 for a diatomic ideal gas.
- TA=300K
- VAVB=16
TB=TA(VAVB)γ−1=300(16)0.4
TB=300×160.4≈300×2.297≈689.1K
2. Use the adiabatic relation:
TDTC=(VCVD)γ−1
Since VD=VA (isochoric process from D to A), we need to find VC first.
- Given VCVB=2, we can express VC in terms of VB:
VC=2VB
- Since VD=VA and VAVB=16:
VD=16VB
VCVD=2VB16VB=18
TD=TC(VCVD)γ−1=TC(18)0.4
- From the isobaric process B to C:
TCTB=VCVB⇒TC=TB⋅VCVB=689.1⋅2≈1378.2K
TD=1378.2(18)0.4≈1378.2⋅0.5≈689.1K
Qs=nCP(TC−TB)
where CP=Rγγ−1.
CP=R⋅1.40.4=3.5R
Qs=1⋅3.5R⋅(1378.2−689.1)≈3.5R⋅689.1
Wnet=Qs−Qr
where Qr is the heat rejected during the isochoric process (D to A).
η=WnetQs⋅100
- Temperature at D: TD≈791K
- Efficiency of the cycle: η≈61.4%
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE MAIN (ARCHIVE )
81 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
- GRAVITATIONBOOK - VMC MODULES ENGLISHCHAPTER - GRAVITATIONEXERCISE - JEE Advance (Archive) TRUE/FALSE
1 Video
Similar Questions
An ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state

View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate the temperature of the gas at point B
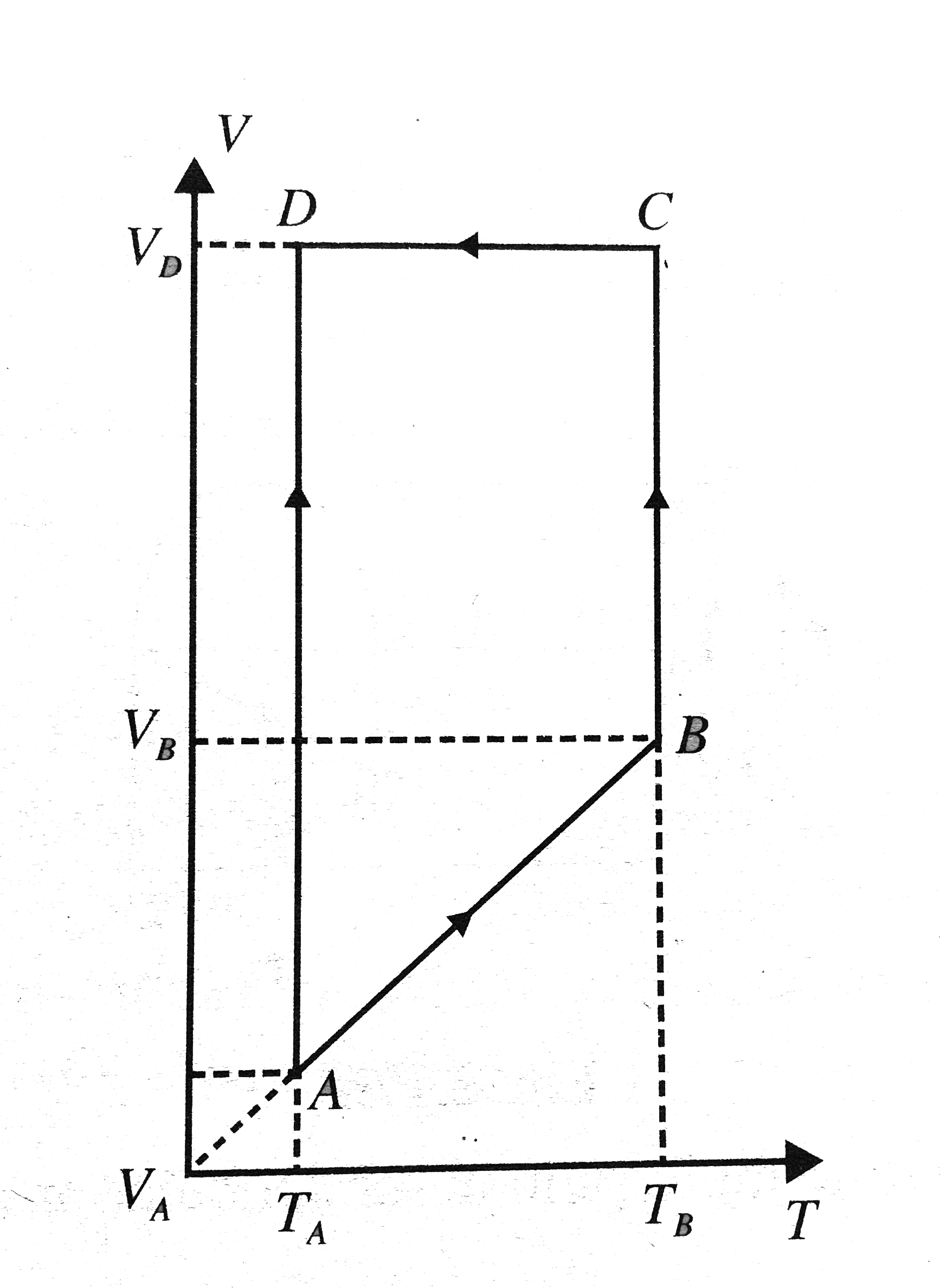
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
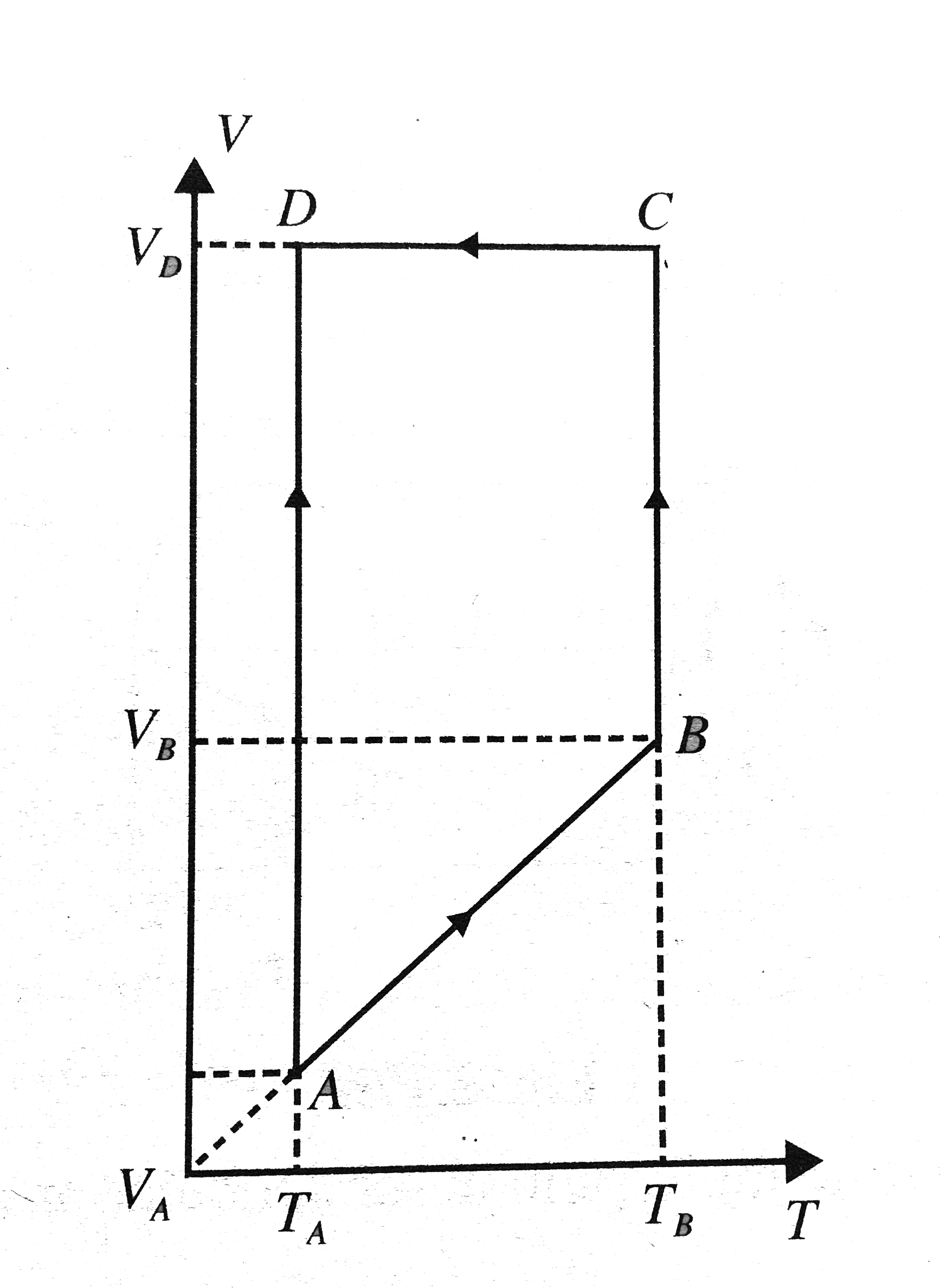
The temperature of the gas at point B
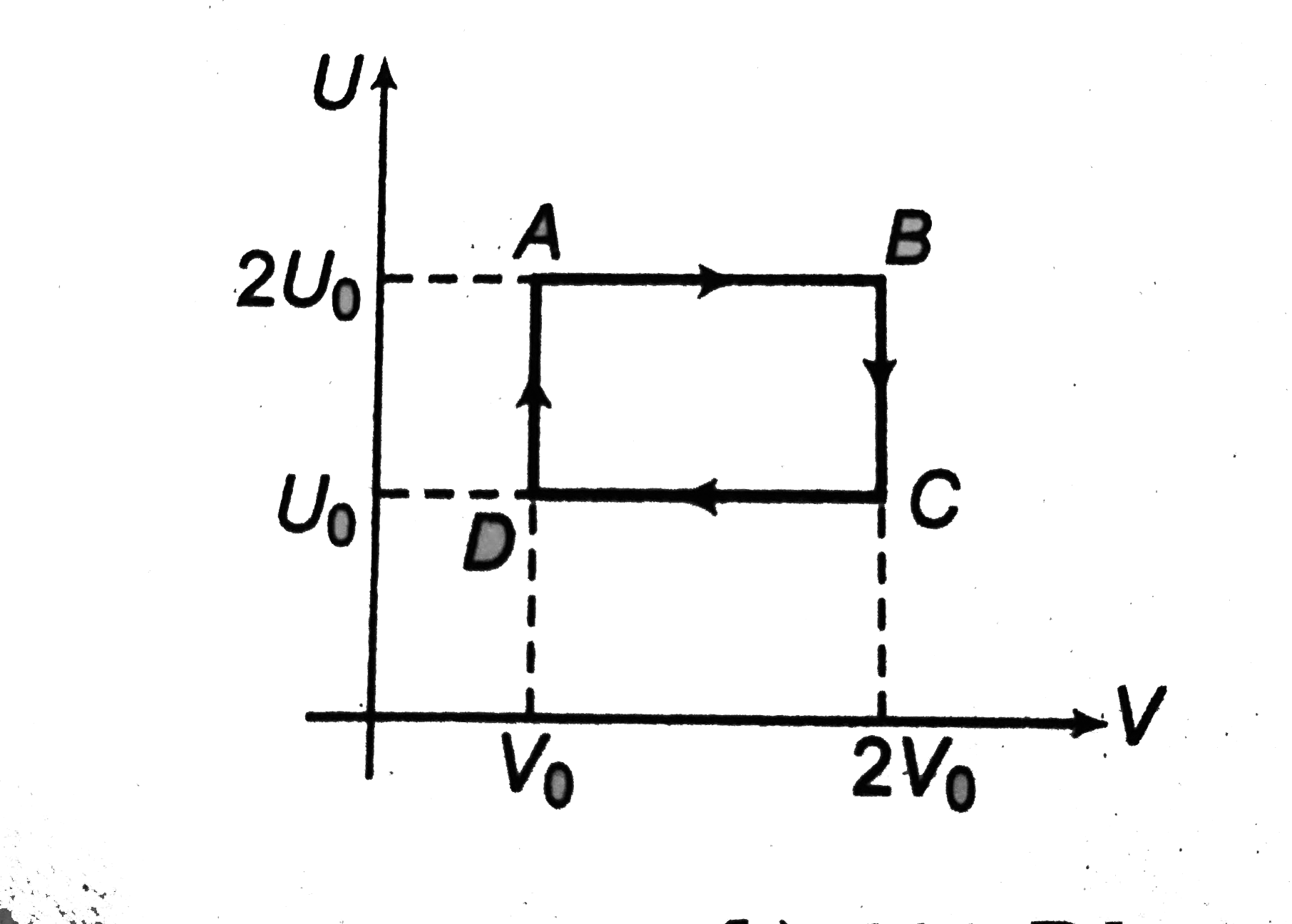
View SolutionOne mole of an ideal gas is taken through a cyclic process. The minimum temperature during the cycle is 300K. Then, net exchange of heat for complete cycle is
View SolutionA mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate
a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total work done in cyclic process.
View SolutionA mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate

a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total wrok done in cyclic process.
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:
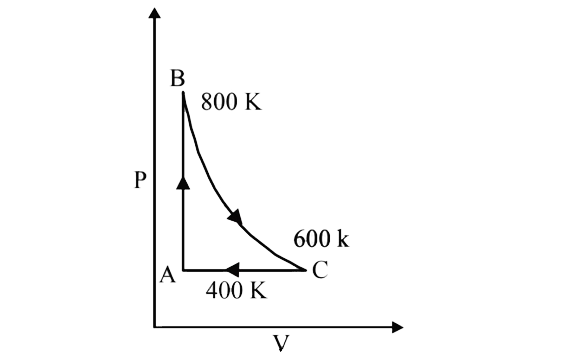
View SolutionOne mole of a diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperature at A,B and C are 400K, 800K and 600K respectively. Choose the correct statement:

View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2 and VDVA=4. If the temperature TA at A is 27∘C, calculate:
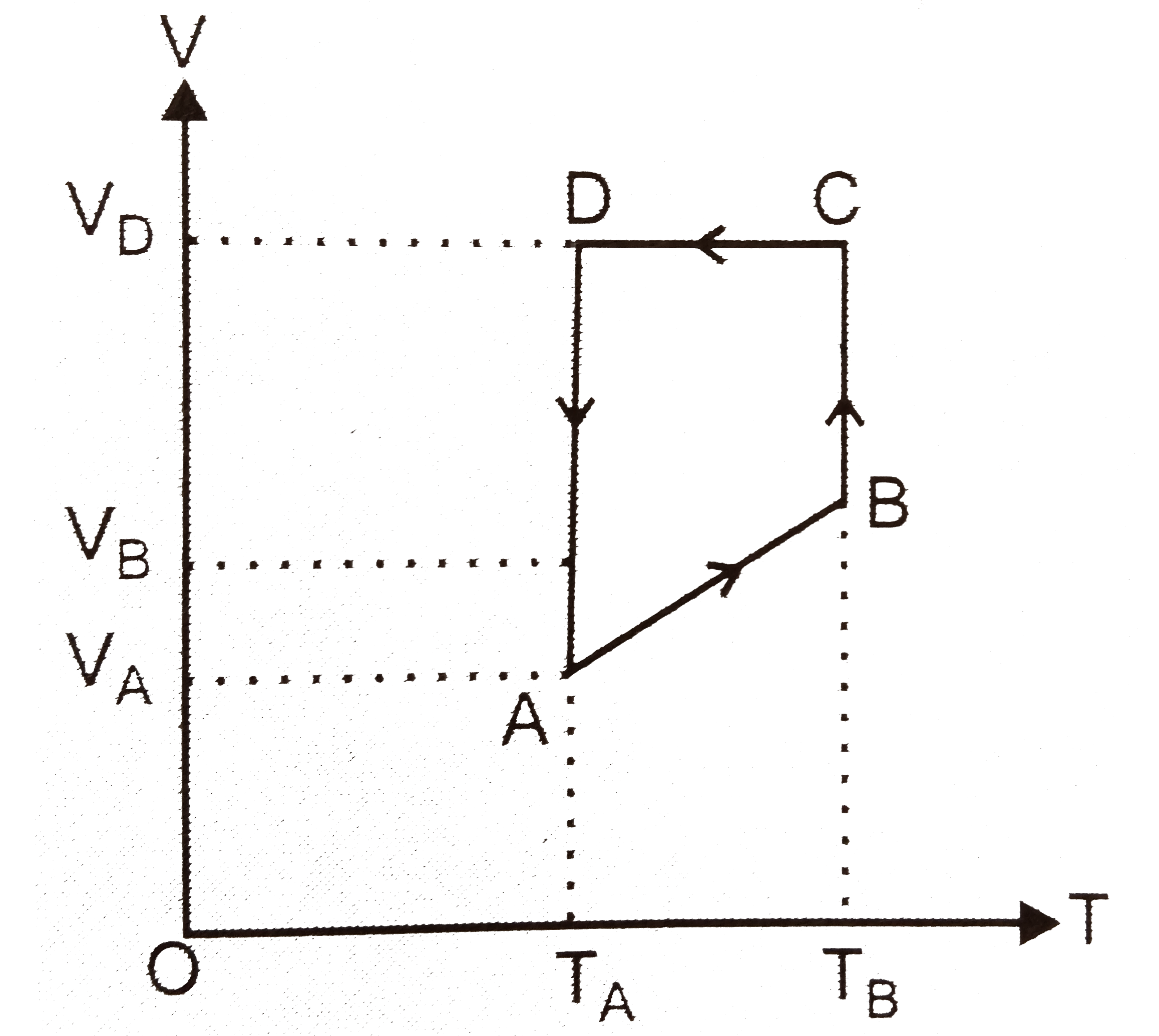
(a) The temperature of the gas at point B.
(b) Heat absorbed or released by the gas in each process.
(c) The total work done by the gas during complete cycle.
View SolutionA monatomic idea gas of 2mol is taken through a cyclic process starting from A as shown in figure. The volume ratio are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C, and gas constant is R. Calculate.
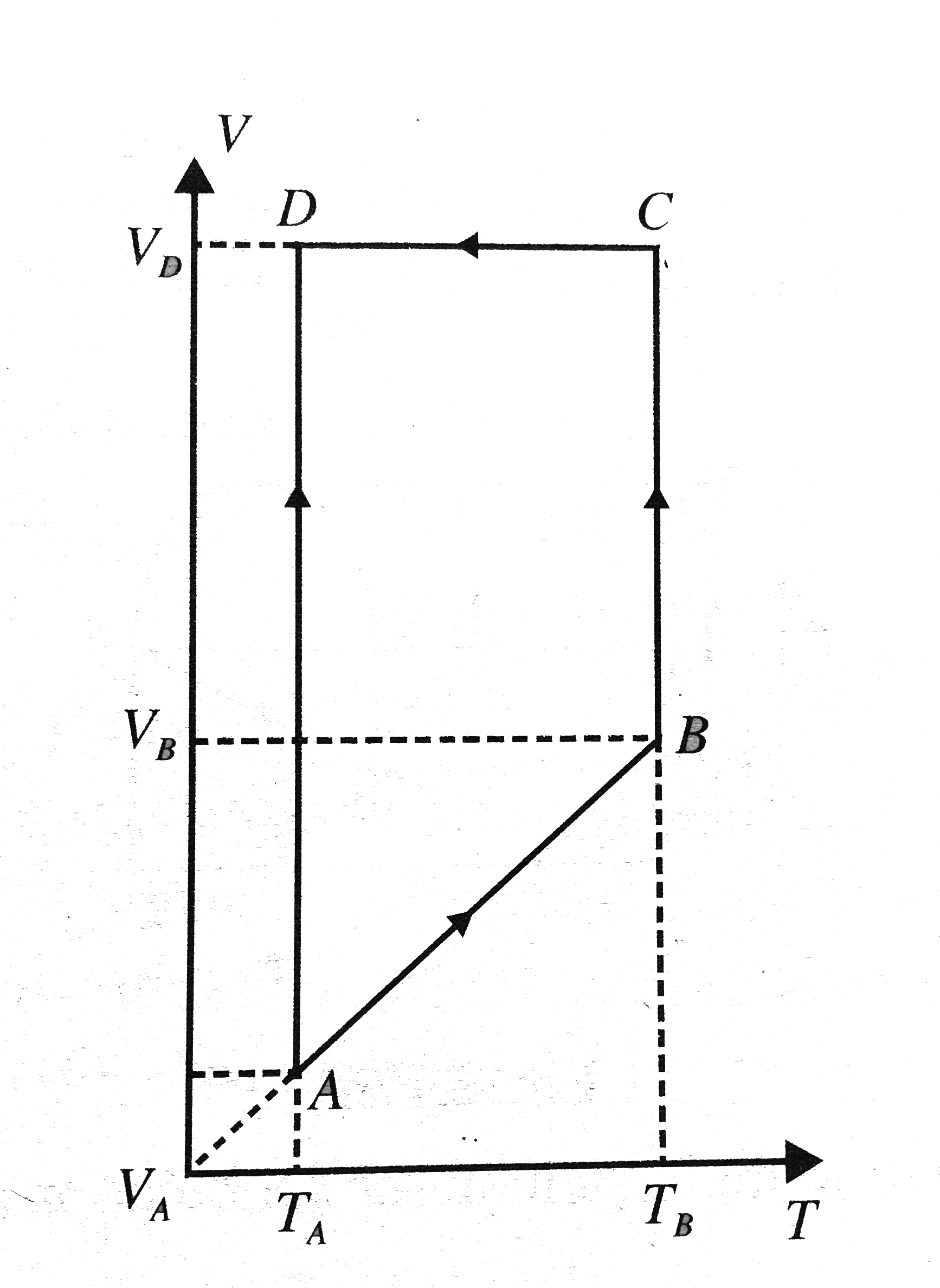
The total work done by the gas during the complete cycle.
View Solution
