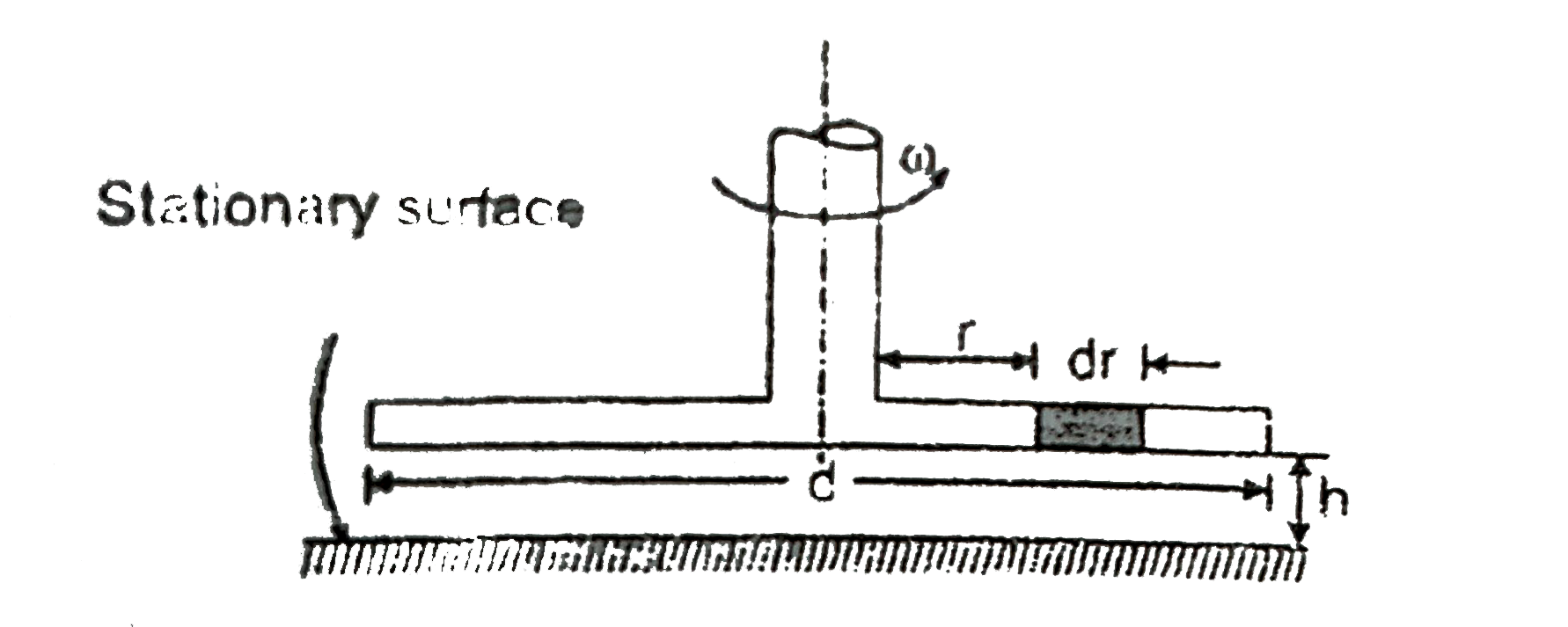
A circular disc of a diameter 'd' slowly rotated in a liquid of large viscosity 'η' at a small distance 'h' from a fixed surface as shown in figure. If an expression for torque 'τ' necessary to maintain an angular velocity 'ω' is πηd4λh then fidn λ.
The correct Answer is:32
dt=η(2πrdrωrh)
t=r∫0ηh2πωr3dr⇒t=∫d/20ηωh2πr3dr
t=[2πηωhr44]d/20⇒t=2πηωhd44×16
t=(πηωd432h)
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - III
Explore 8 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 3 PART - I
Explore 7 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Exercise- 2 PART - I
Explore 9 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 92 illustration
Explore 2 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercise
Explore 43 Videos
Similar Questions
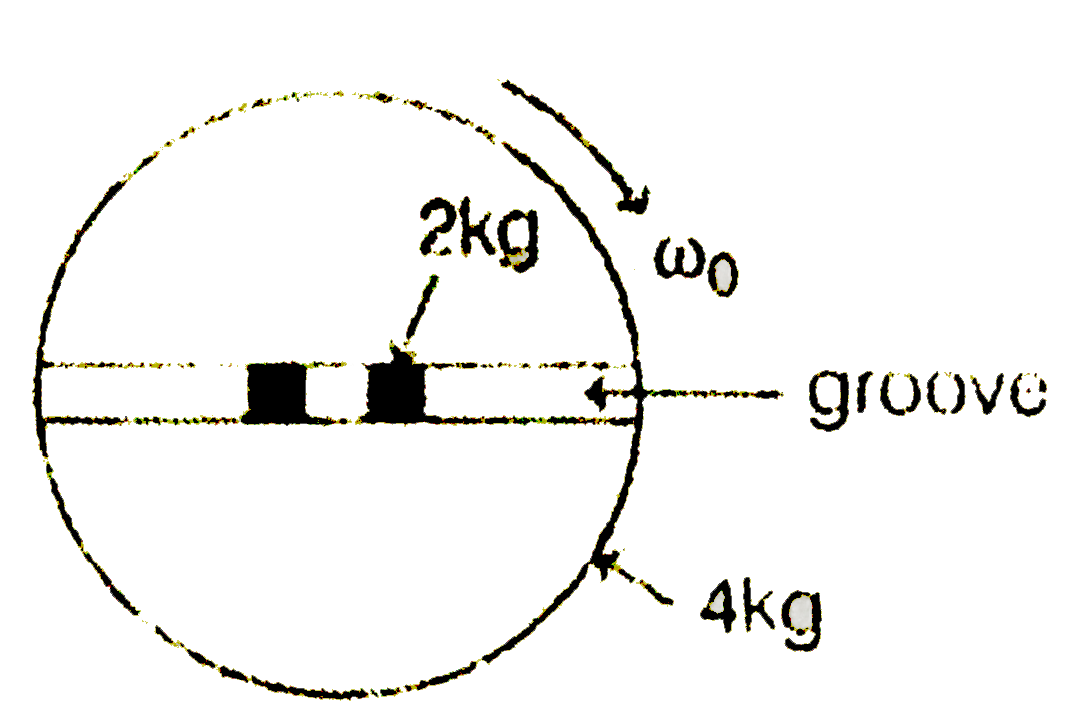
A disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The difference in the heights (h) of the liquid column in the two vertical thin tubes is :
View SolutionA horizontal thin tube of length 2L completely filled with a liquid of density δ rotates about a vertical axis passing through one of its end and along the diameter of its side face with an constant angular velocity ω. Two vertical thin long tubes are fitted with the horizontal tube to measure the pressure difference between points A and B which are at same horizontal level as shown. Neglect viscous forces and surfaces tension of liquid.

The graph of the pressure gradient (dPdx) with the distance x meaured from the axis of rotation is :
View SolutionA thin plate AB of large area A is placed symmetrically in a small gap of height h filled with water of viscosity η0and the plate has a constant velocity v by applying a force F as shown in the figure. If the gap is filled with some other liquid of viscosity 0.75η0 at what minimum distance (in cm) from top wall should the plate be placed in the gap, so that the plate can again be pulled at the same constant velocity V. by applying the same force F? (Take h=20cm)
View SolutionA uniform circular disc placed on a horizontal rough surface has initially a velocity v0 and an angular velocity ω0 as shown in the figure. The disc comes to rest after moving some distance in the direction of motion. Then v0/rω0 is :

View SolutionA uniform circular disc placed on a horizontal rough surface has initially a velocity v0 and an angular velocity ω0 as shown in the figure. The disc comes to rest after moving some distance in the direction of motion. Then v0/ω0 is :

View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View SolutionA smooth disc of mass M and radius L√3 is placed at rest horizontally on a smooth horizontal surface. A massless pin is fixed at point P at a distance L/2 from centre O of the disc as shown in the figure. Now a thin uniform rod of mass M and length L is placed horizontally on the surface of the disc parallel to the line OP such that its mid point and centre O of the disc just coincide as shown in figure. Now rod has given angular velocity ω0=24rad/sec in counter clockwise direction as shown. As a result, the end of the rod strikes the pin P and stricks to it rigidly. Calculate the angular velocity of disc just after collision.

View SolutionA metal rod OA of mann 'm' and length 'r' is kept rotating with a constantangular speed ω in a vertical plane about a horizontal axis at the end O. The free end A is arraged to slide without friction along fixed conduction circular ring in the same plane as that of rotation. A uniform and constant magnetic induction →B is applied perpendicular and into the plane of rotation as shown in the figure below. An inductor L and an external resistance R are connected through a swithch S between the point O and a point C on the ring to form an electrical circuit. Neglect the resistance of the ring and the rod. Initially, the switch is open.
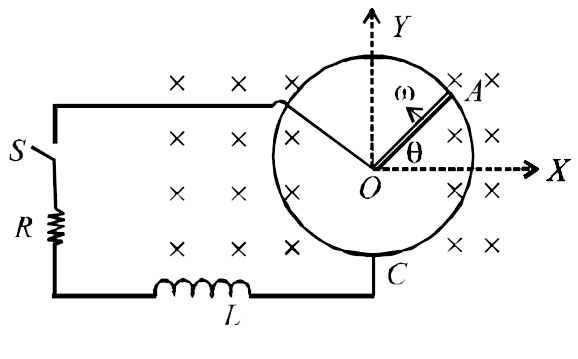
(a) What is the induced emf across the teminal of the switch?
(b) The switch S is closed at time t=0.
(i) Obtain an expression for the current as a function of time.
(ii) In the steady state, obtin the time dependence of the torque required to maintain the constant angular speed, given that the rod OA was along th positive X-axis at t=0.
View Solution

