
a cavity of radius R is taken out from a uniformly charged solid sphere with charge density ρ and radius 2R as shown Consider four points 1,2,3,4 at following positions,
1-(2R,0,0)
2- (R,0,0) ltbr> 3- (0,0,0)
4- (3R,0,0)
E1,E2,E3,E4 represents magnitude of net electric field at 1,2,3,4 respectively then the correct option (s) are:
a.E1E2=E2E3
b.E4E2=43
c.E4E1=34
d.E4E2=34
The correct Answer is:A, B, C
E=ρr3ε0 [for inside cavity points] &
(ρR33ε0r2 for out side cavity points)
E1=E2=E3=ρR3ε0
E4=ρR3ε0−ρ(R)33ε0(2R)2
=ρR3ε0−ρR3ε0×4=ρR4ε0
Similar Questions
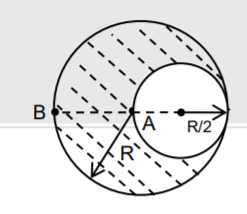
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionA solid non conducting sphere of radius R and uniform volume density ρ has centre at origin. Find out electric field intensity in vector form at following positions :
(i) (R, 0, 0) (ii) (0, 0, R/2) (iii) (R, R, R)
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View SolutionA uniformly charged solid sphere of radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere the equipotential surfaces with potentials 3V02,5V04,3V04 and V04 have radius R1,R2,R3 and R4 respecatively. Then
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
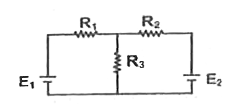
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3

View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View SolutionA solid insulating sphere of radius R has a nonuniform charge density that varies with r according to the expression ρ=Ar2, where A is a constant and r<R is measured from the centre of the sphere. Show that (a) the magnitude of the electric field outside (r>R) the sphere is E=AR5/5ε0r2 and (b) the magnitude of the electric field inside (r<R) the sphere is E=Ar3/5ε0.

View Solution