A trolley filled with sand is moving with a velocity v on a smooth horizontal surface due to inertia. If the sand falls off at the rate of μkg/sec, the velocity of the trolley as a function of time will be best represented by:

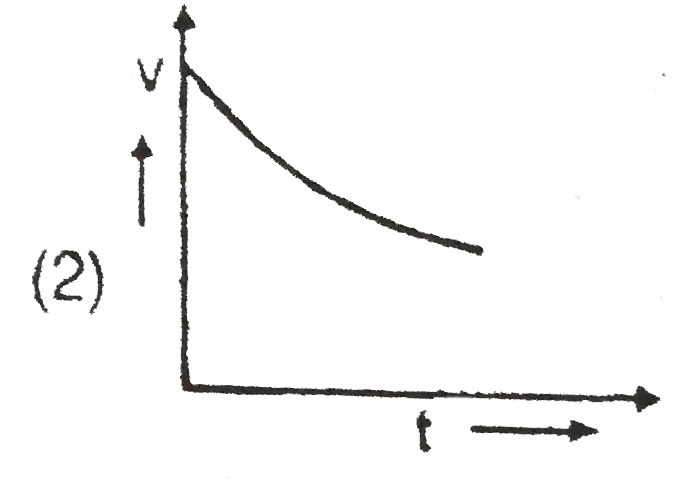
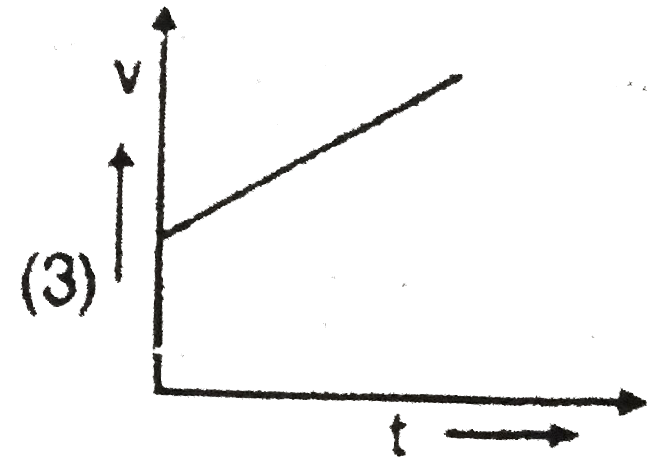

The correct Answer is:D
To solve the problem, we need to analyze the motion of the trolley filled with sand as the sand falls off. We will use the principle of conservation of momentum to derive the velocity of the trolley as a function of time.
1. Initial Conditions:
- Let the initial mass of the trolley filled with sand be M.
- The initial velocity of the trolley is v.
- The sand falls off at a rate of μ kg/s.
2. Mass of the Trolley Over Time:
- After time t, the mass of the sand that has fallen off is μt.
- Therefore, the mass of the trolley at time t is given by:
Mt=M−μt
3. Conservation of Momentum:
- According to the conservation of momentum, the total momentum before the sand falls must equal the total momentum after the sand starts falling.
- Initially, the momentum of the system (trolley + sand) is:
Pinitial=M⋅v
- After time t, the momentum of the trolley (with mass M−μt moving with velocity v′) and the falling sand (with mass μt moving with the same velocity v′) is:
Pfinal=(M−μt)⋅v′+μt⋅v′
- Simplifying this, we get:
Pfinal=(M−μt+μt)⋅v′=M⋅v′
4. Setting Initial and Final Momentum Equal:
- By conservation of momentum, we set the initial and final momentum equal:
M⋅v=M⋅v′
- Since M is not zero, we can divide both sides by M:
v=v′
5. Conclusion:
- This shows that the velocity of the trolley remains constant over time, regardless of the sand falling off. Thus, the velocity of the trolley as a function of time is:
v(t)=v
Final Answer:
The velocity of the trolley as a function of time remains constant and is given by:
v(t)=v
- Let the initial mass of the trolley filled with sand be M.
- The initial velocity of the trolley is v.
- The sand falls off at a rate of μ kg/s.
- After time t, the mass of the sand that has fallen off is μt.
- Therefore, the mass of the trolley at time t is given by:
Mt=M−μt
- According to the conservation of momentum, the total momentum before the sand falls must equal the total momentum after the sand starts falling.
- Initially, the momentum of the system (trolley + sand) is:
Pinitial=M⋅v
- After time t, the momentum of the trolley (with mass M−μt moving with velocity v′) and the falling sand (with mass μt moving with the same velocity v′) is:
Pfinal=(M−μt)⋅v′+μt⋅v′
- Simplifying this, we get:
Pfinal=(M−μt+μt)⋅v′=M⋅v′
- By conservation of momentum, we set the initial and final momentum equal:
M⋅v=M⋅v′
- Since M is not zero, we can divide both sides by M:
v=v′
- This shows that the velocity of the trolley remains constant over time, regardless of the sand falling off. Thus, the velocity of the trolley as a function of time is:
v(t)=v
The velocity of the trolley as a function of time remains constant and is given by:
v(t)=v
Topper's Solved these Questions
Similar Questions
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA cart loaded with sand moving with velocity v. Sand is falling through the hole as shown in diagram then after falling on the ground sand is
View SolutionA block of mass 5 kg is at rest on a smooth horizontal surface. Water coming out of a pipe horizontally at the rate of 2 kgs−1 , hits the block with a velocity of 6ms−1.The initial acceleration of the block is,
View SolutionA block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0+ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionA small body of mass m moving with velocity v0 on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient μ=0.27,m=1 kg and v0=1.5ms−1.
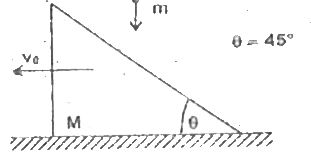
View SolutionA triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
View SolutionA cubical tanker completely filled with water is moving with a constant velocity. A hole develops at the bottom in its horizontal surface through which water comes out. 4kg of water leaks out in 30 seconds. If the velocity of truck becomes x times of its initial velocity then find x.
View SolutionA uniform rod PQ of mass m and length t rotates with an angular velocity a while its center moves with linear velocity v=2ω⋅f3 on a smooth horizontal surface If the end Q of the rod is suddenly gets stuck at the moment as shown in the figure then angular velocity of the rod will be
View SolutionA container filled with liquid up to height h is placed on a smooth horizontal surface. The container is having a small hole at the bottom. As the liquid comes out from the hole, the container moves in a backward direction with acceleration a and finally, when all the liquid is drained out, it acquires a velocity v. Neglect mass of the container. In this case

View SolutionA tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. From the plot shown in figure, indicate the one that represents the velocity (v) of the pebble as a function of time (t)
View Solution
