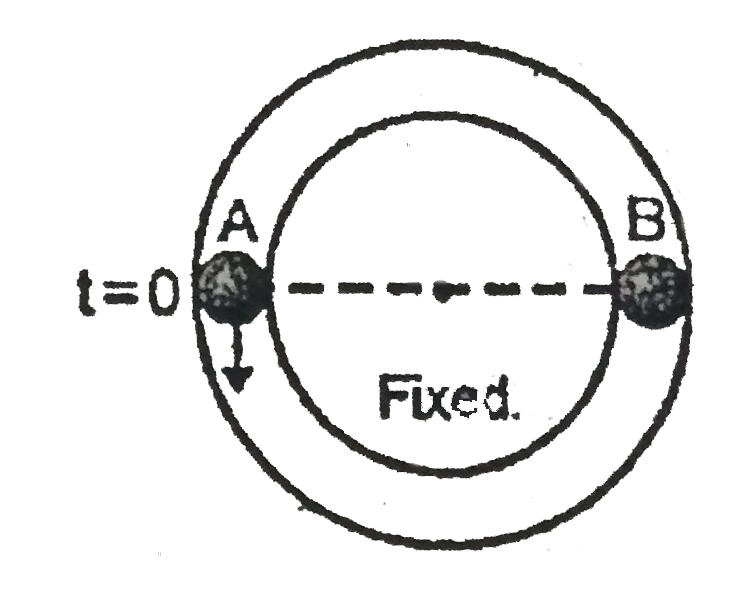
Particle 'A' moves with speed 10 m/s in a frictionless circular fixed horizontal pipe of radius 5 m and strikes with 'B' of double mass that of A. Coefficient of restitution is 1/2 and particle 'A' starts its journet at t = 0. The time at which second collision occurs is :

π2s
2π3s
5π2s
4πs
The correct Answer is:C
For first collision v =10 m/s t1=π(5)10=π/2sec.
velocity of separation =e. velocity of approach.
v2−v1=12(10)⇒v2−v1=5m/s
For second collision
∴t2=2π(5)5=2π
∴ Total time t=t+t2=π/2+2π⇒t=2.5π
Topper's Solved these Questions
Similar Questions
Particle 'A' moves with speed 10m/s in a frictionless circular fixed horizontal pipe of radius 5m and strikes with 'B' of double mass that of A. Coefficient of restitution is 12 and particle 'A' -starts its journey at t=0. The time at which second collision occurs is:
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Velocity of B after collision
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then
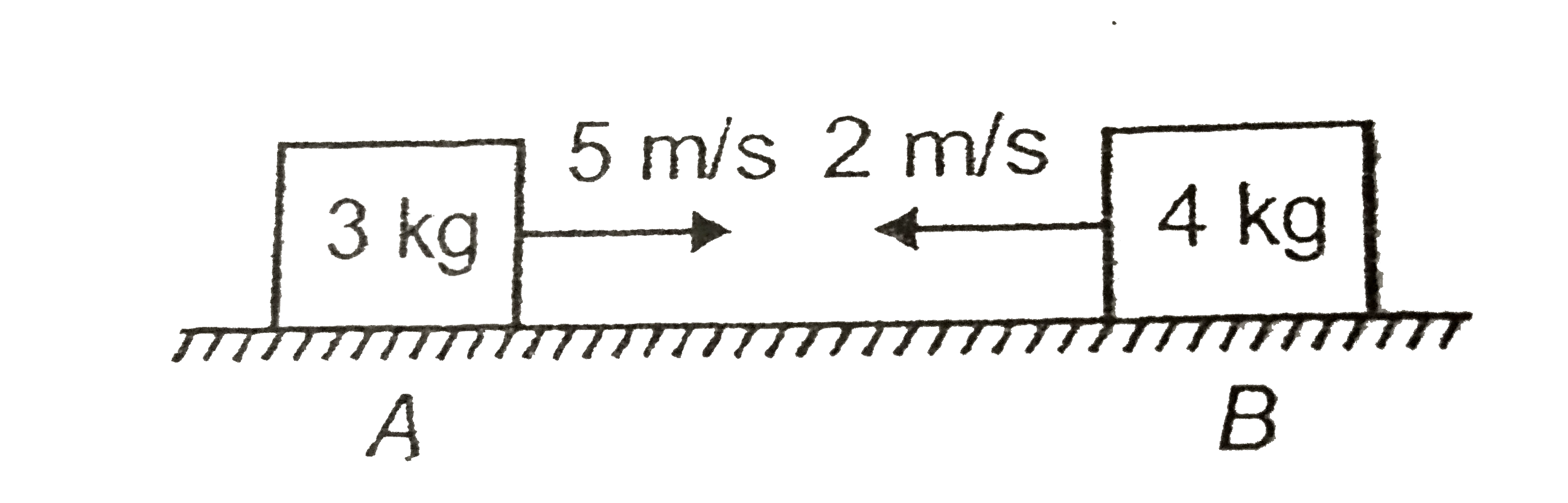
Velocity of A after collision
View SolutionA vehicle is moving at a speed of 30 m/s on a circular road of radius 450 m. Its speed is increasing at a rate of 2ms2 . The acceleration of particle at this instant is
View SolutionTwo particles A and B of mass 3kg and 4kg moving on a smooth horizontal surface with speed 5m/s and 2m/s respectively collides each other. Coefficient of restitution is e=12, then

Loss in kinetic energy in collision
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
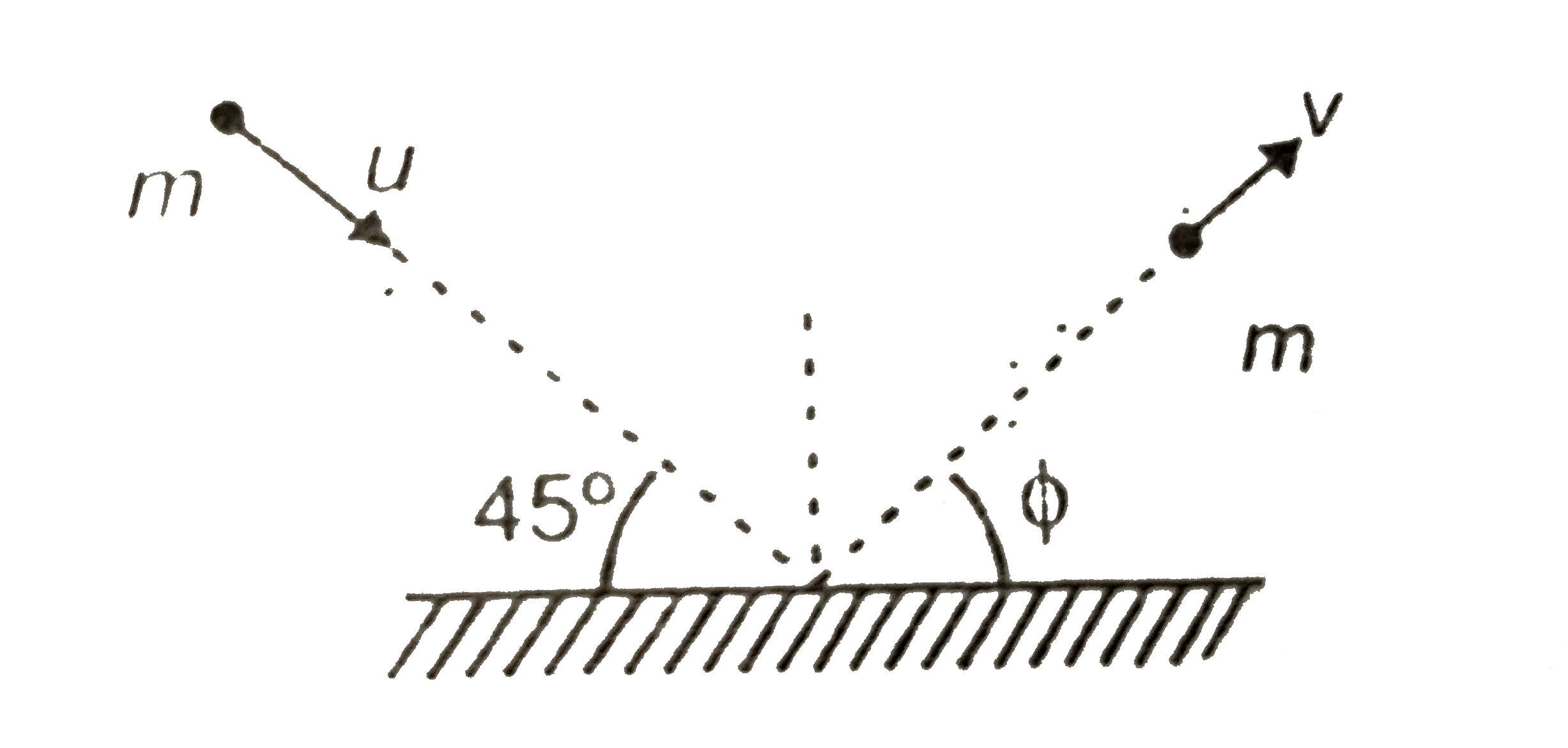
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is

View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View Solution