A triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
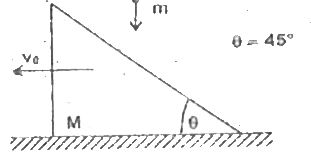
Line of impact is a straight line perpendicular to the incline. Normal reaction force between the body and the wedge acts along the impact line. This normal force becomes internal force when we consider (wedge + body) as a total system. But normal reaction is considerable in magnitude because the impact force during collision has contribution towards making of the normal force. Momentum of the system is conserved along the line perpendicular to this normal force. ....(i)
Momentum of the system is conserved along horizontal .....(ii)
Momentum of the particle is conserved along the common tangent at the point of impact. .....(iii)
As this is an elastic collision, relative velocity of separation along the impact line = Relative velocity of approach. .....(iv)
If the wedge were at rest then the particle would deflect along the horizontal after collision because it is an elastic collision .....(v)
As, in this case, wedge is moving, the object would not be deflected horizontal, but at an angle .α. to the line of impact ....(vi)
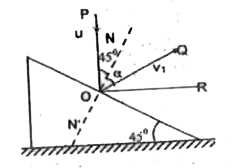
Velocity of particle before impact u=√2gh along −−→PO
Velocity of particle after collision =v1 along −−→OQ
Velocity of wedge before collision =v0 along −−→RO
Velocity of wedge after collision =v2 along −−→RO
Velocity of approach = velocity of separation
v0cos45∘−ucos45∘=−v1cosα−v2cos45∘
⇒v1cosα+v2√2=u√2−v0√2
√2v1cosα+v2=u−v0 ....(A)
Conserving momentum along the horizontal
Mv0=Mv2−mv1cos(45∘−α)
⇒2v0=2v2−v1cos(45∘−α)
⇒2v2−v1cos(45∘−α)=2v0 ....(B)
Conserving momentum along the common tangent
μsin45∘=mv1sinα
⇒v1sinα=u ....(C )
On solving (A), (B) and (C )
v1=
⎷u2⎡⎢
⎢⎣u(4−√2)−6v020⎤⎥
⎥⎦2 and v2=v0+(√2+1)u5
Similar Questions
Two particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View Solution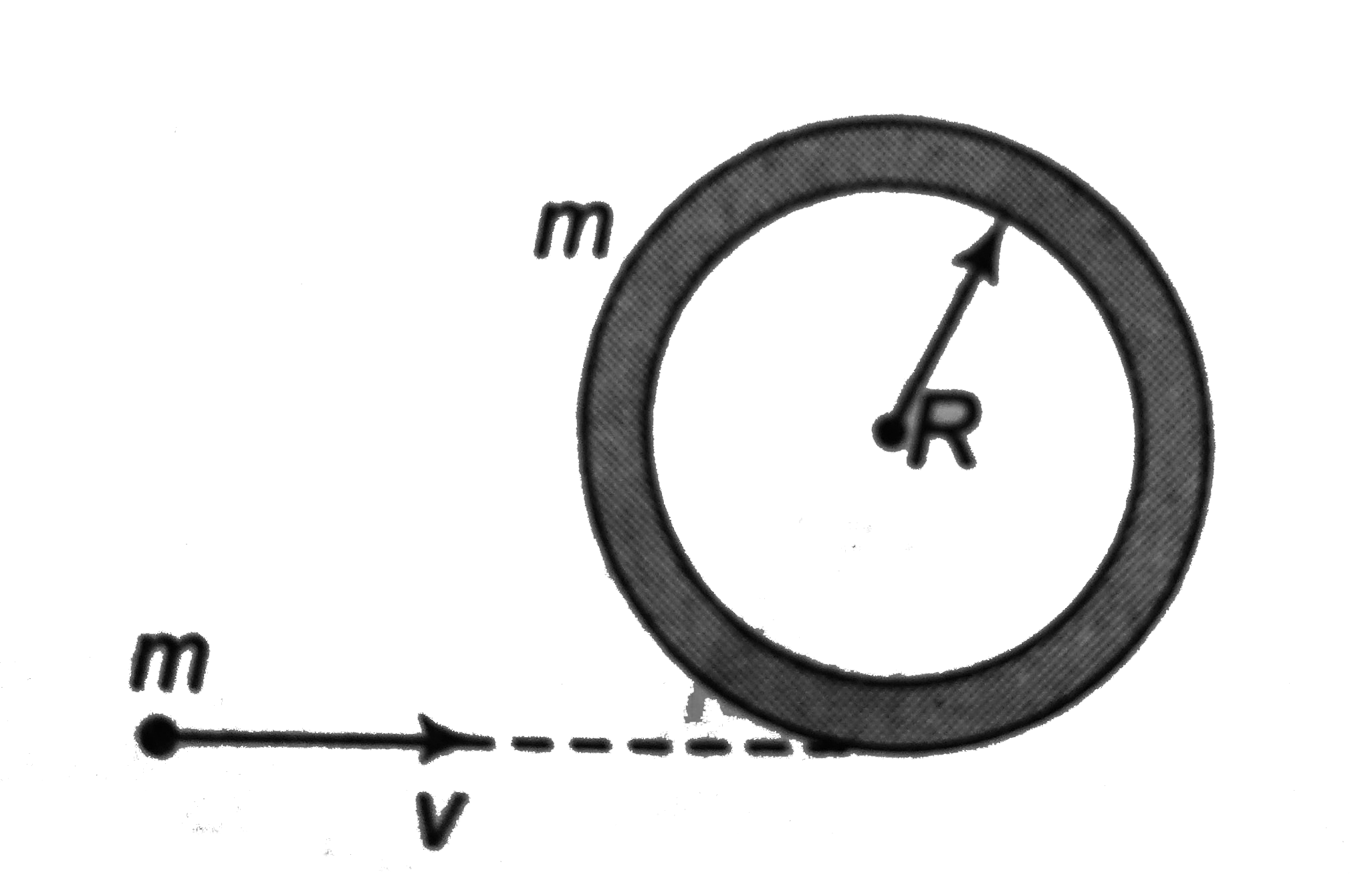
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionTwo balls of masses m and 2m moving in opposite directions collide head on elastically with velocities v and 2v. Find their velocities after collision.
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

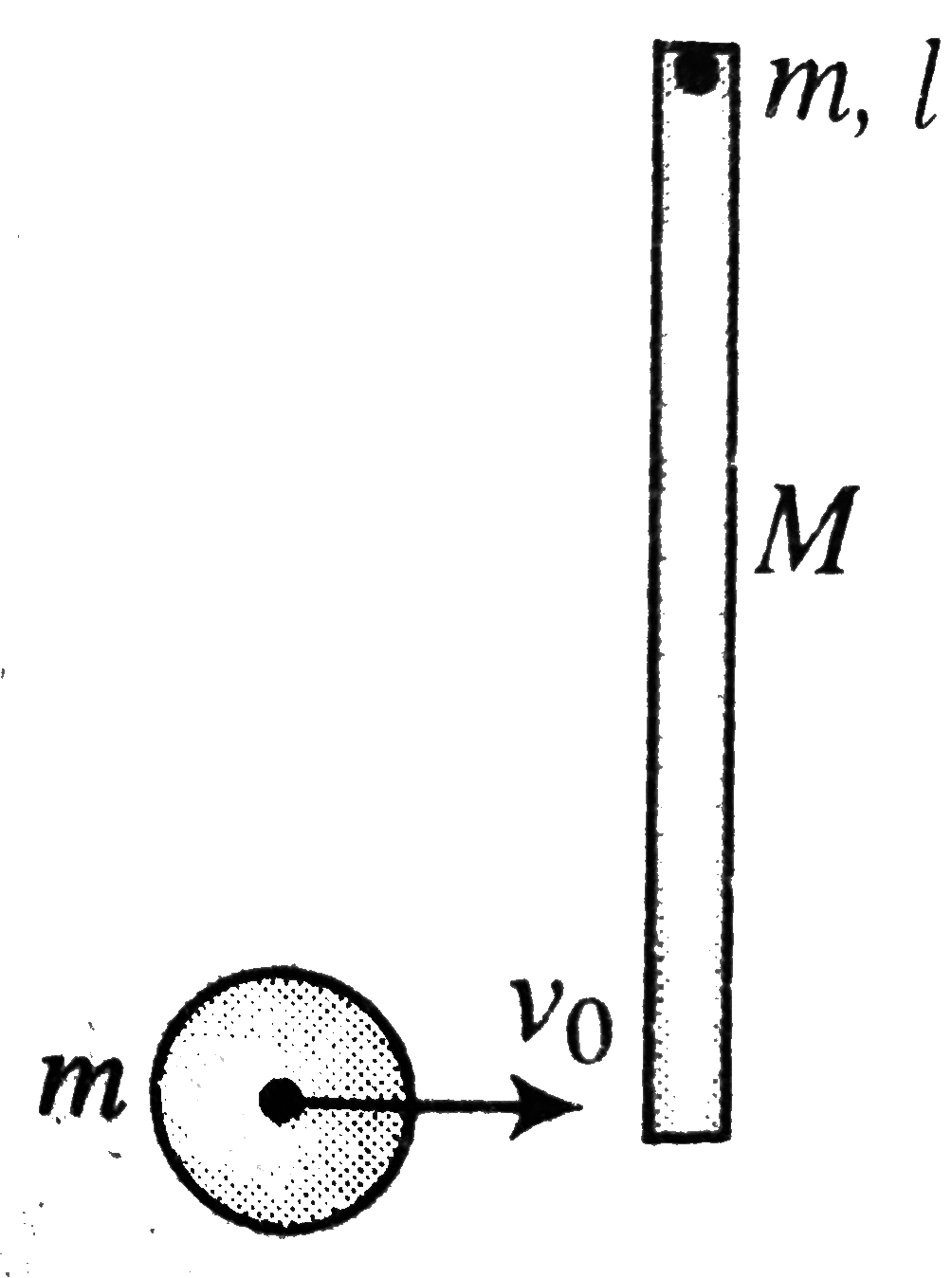
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View Solution
