Initially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
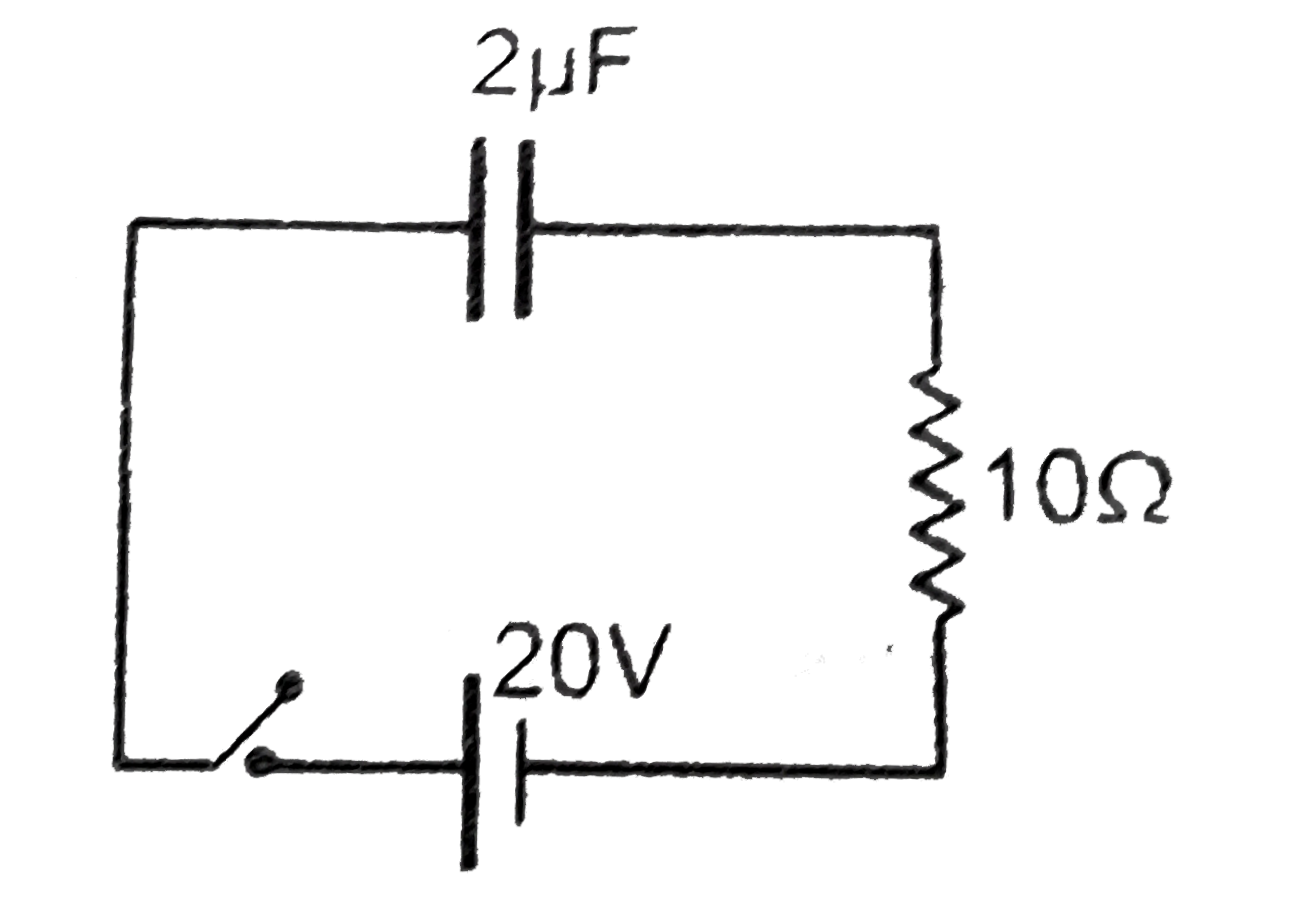
4μC
8μC
36μC
16μC
The correct Answer is:C
Maximum current in the circuit is
2010=2A
when current is 0.2 A

Apply KVL-
−q2−0.2×10+20=0⇒q=36μC
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.50
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.51
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.48
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionIn the circuit arrangement shown in figure capacitor is initially unchanged At t = 0 switch is thrown to position '1' it remains closed till the current in the circuit becomes 50 % of maximum current then. Suddenly switch is shifted to position '2' (Assume all batteries are ideal)
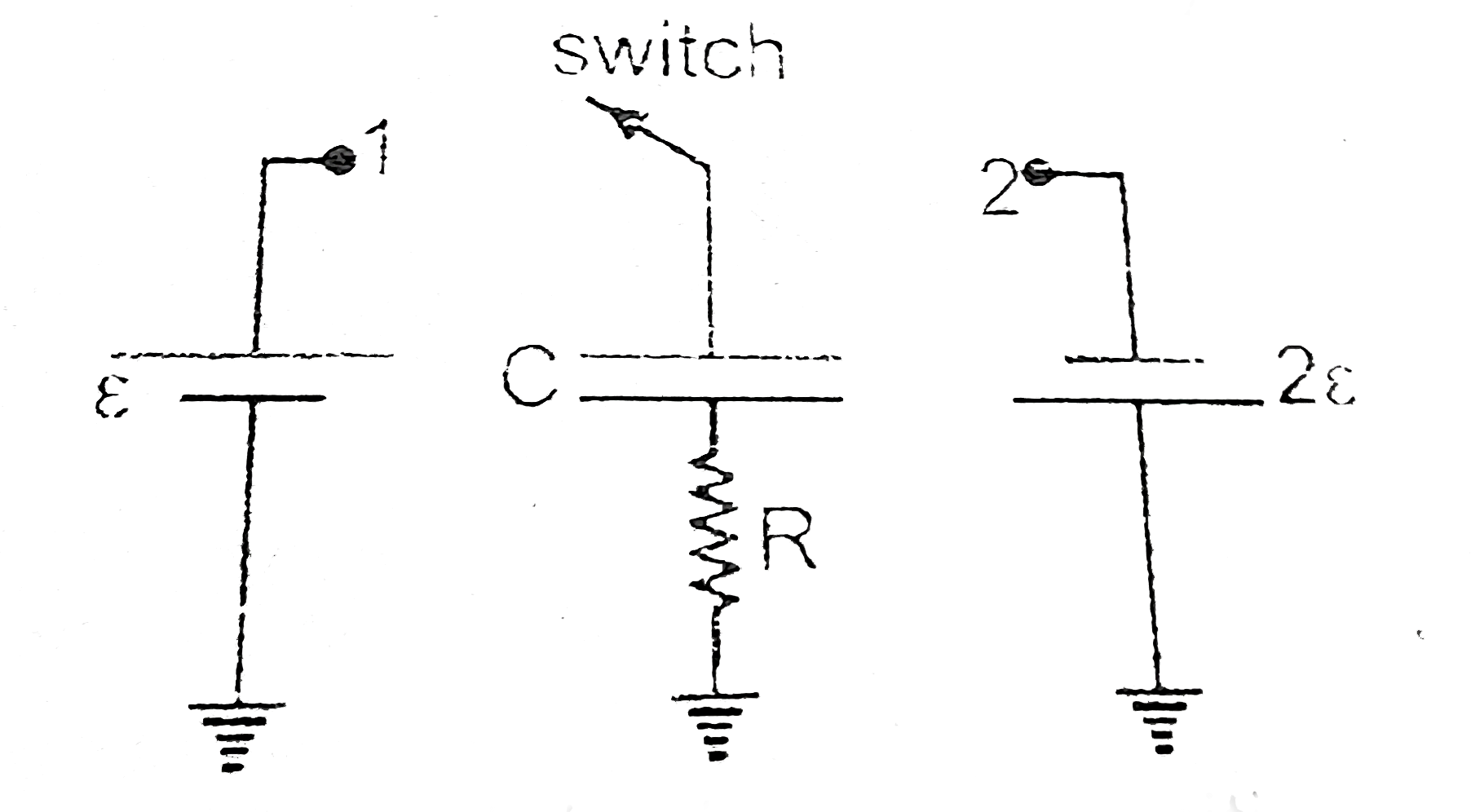
Current through the resistor just after switch is shifted to position '2' is :
View SolutionIn the circuit arrangement shown in figure capacitor is initially unchanged At t = 0 switch is thrown to position '1' it remains closed till the current in the circuit becomes 50 % of maximum current then. Suddenly switch is shifted to position '2' (Assume all batteries are ideal)

Amount work done by battery long after switch is shifted to position '2' is :
View SolutionIn the circuit arrangement shown in figure capacitor is initially unchanged At t = 0 switch is thrown to position '1' it remains closed till the current in the circuit becomes 50 % of maximum current then. Suddenly switch is shifted to position '2' (Assume all batteries are ideal)

Which of the following is the correct options after switch is shifted to position '2'.
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View Solution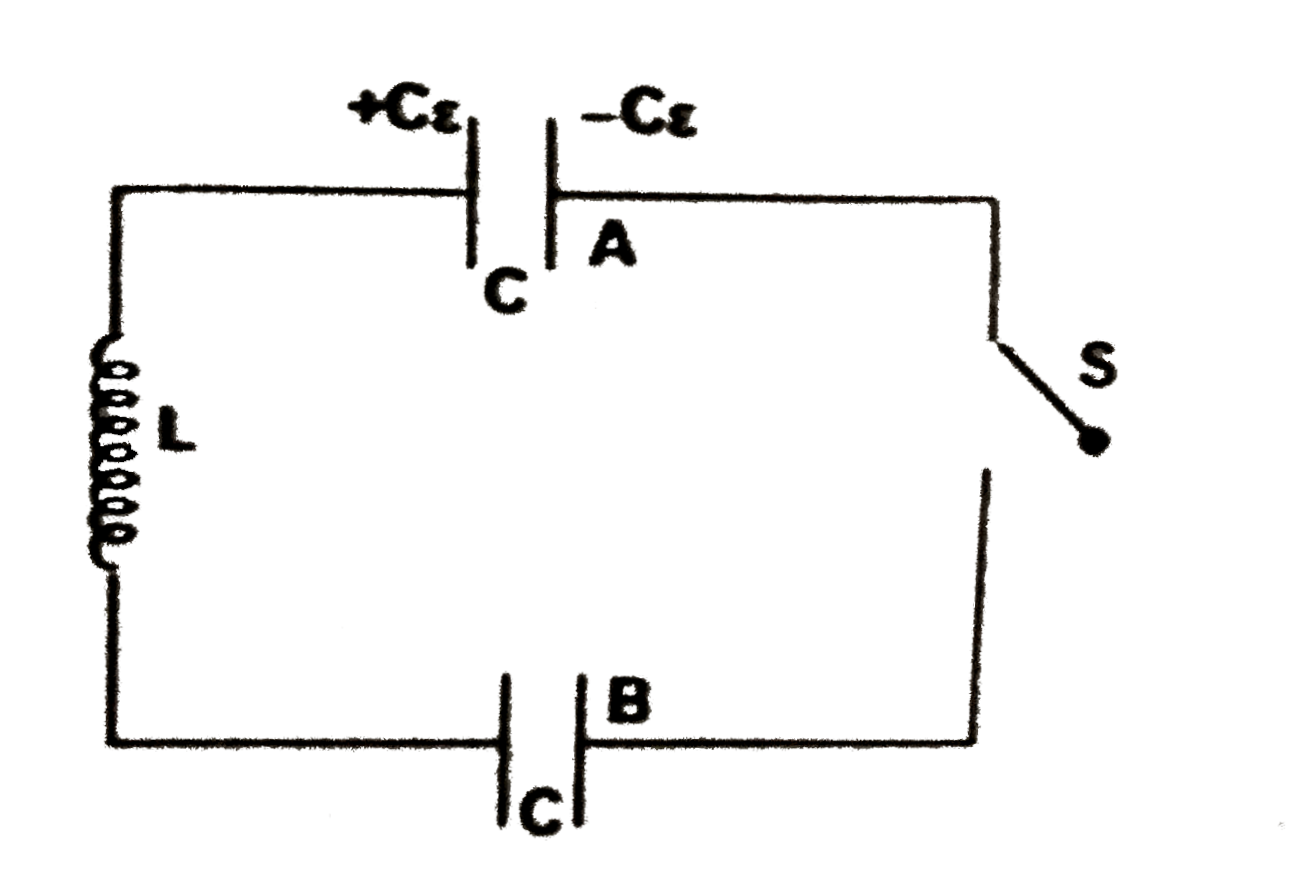
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionIf maximum energy is stored in capacitor at t = 0 then find the time after which current in the circuit will be maximum.
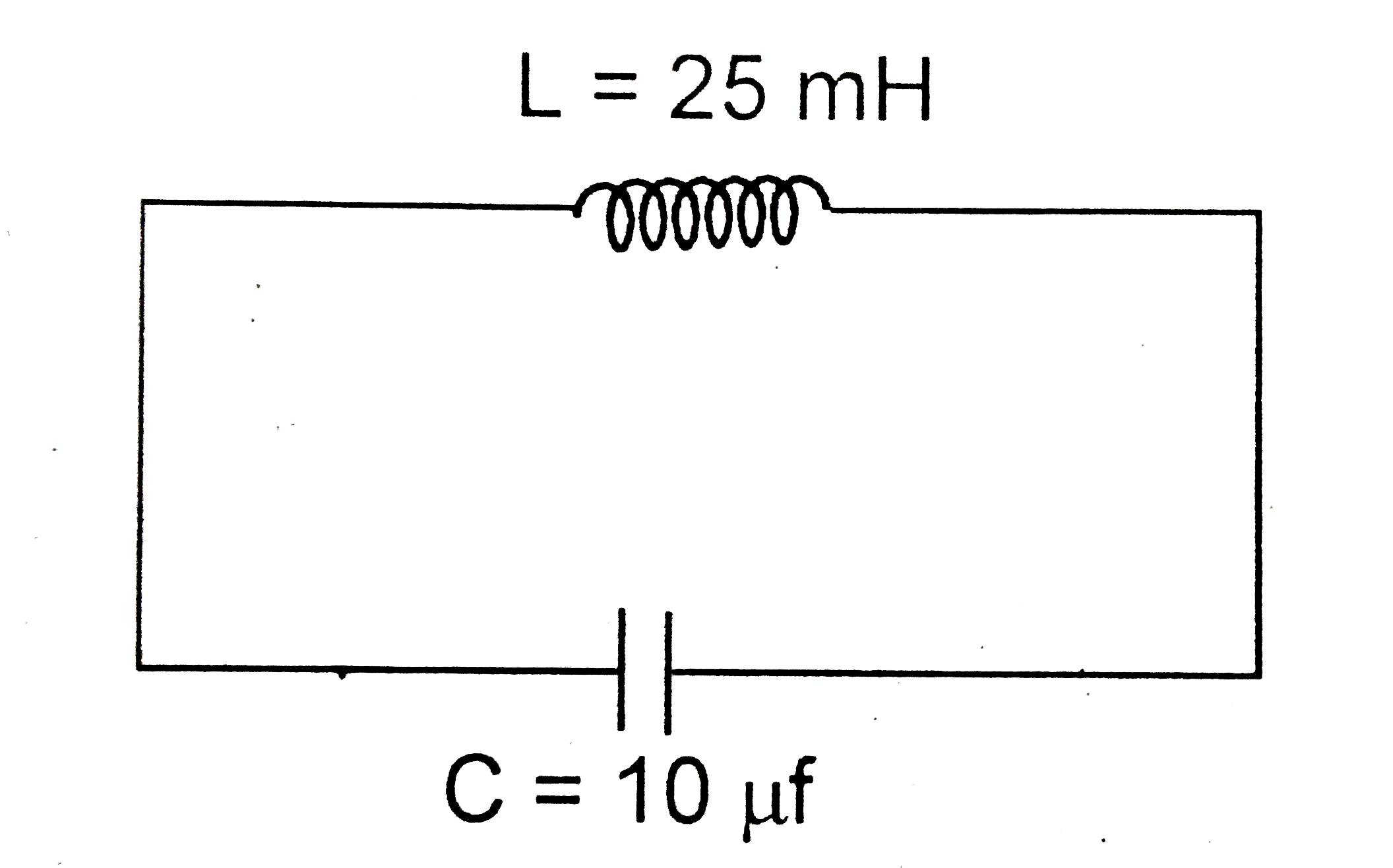
View SolutionA charged capacitro and an inductor are connected in series. At time t = 0 , the current is zero but the capacitor is charged, If T is the period of resulting oscillations, then the time after which current in the circuit becomes maximum , is
View Solution
