The figure shows a meter bridge circuit with AB=100 cm, X=12ΩandR=18Ω and the jockey J in the position of balance. If R is now made 8Ω through what distance will J have to be moved to obtain balance?
10 cm
20 cm
30 cm
40 cm
The correct Answer is:B
To solve the problem, we will use the principle of the meter bridge, which is based on the Wheatstone bridge principle. The balance condition can be expressed in terms of the lengths on the meter bridge and the resistances connected.
1. Identify the Initial Conditions:
- Given:
- Length of the meter bridge, AB=100cm
- Resistance X=12Ω
- Resistance R=18Ω
- Let the length from point A to the jockey position be L.
2. Apply the Balance Condition:
- According to the balance condition of the meter bridge:
RX=100−LL
- Substituting the values of R and X:
1812=100−LL
- Simplifying the left side:
32=100−LL
3. Cross-Multiply to Solve for L:
- Cross-multiplying gives:
3L=2(100−L)
- Expanding the right side:
3L=200−2L
- Rearranging the equation:
3L+2L=200
5L=200
L=2005=40cm
4. Change the Resistance R:
- Now, we change R to 8Ω.
- We need to find the new length L′ when R=8Ω:
RX=100−L′L′
- Substituting the new value of R:
812=100−L′L′
- Simplifying the left side:
23=100−L′L′
5. Cross-Multiply to Solve for L′:
- Cross-multiplying gives:
2L′=3(100−L′)
- Expanding the right side:
2L′=300−3L′
- Rearranging the equation:
2L′+3L′=300
5L′=300
L′=3005=60cm
6. Calculate the Distance the Jockey Needs to Move:
- The distance ΔX that the jockey has to move is:
ΔX=L′−L=60cm−40cm=20cm
Final Answer:
The jockey has to be moved by 20 cm to obtain balance when R is changed to 8Ω.
---
- Given:
- Length of the meter bridge, AB=100cm
- Resistance X=12Ω
- Resistance R=18Ω
- Let the length from point A to the jockey position be L.
- According to the balance condition of the meter bridge:
RX=100−LL
- Substituting the values of R and X:
1812=100−LL
- Simplifying the left side:
32=100−LL
- Cross-multiplying gives:
3L=2(100−L)
- Expanding the right side:
3L=200−2L
- Rearranging the equation:
3L+2L=200
5L=200
L=2005=40cm
- Now, we change R to 8Ω.
- We need to find the new length L′ when R=8Ω:
RX=100−L′L′
- Substituting the new value of R:
812=100−L′L′
- Simplifying the left side:
23=100−L′L′
- Cross-multiplying gives:
2L′=3(100−L′)
- Expanding the right side:
2L′=300−3L′
- Rearranging the equation:
2L′+3L′=300
5L′=300
L′=3005=60cm
- The distance ΔX that the jockey has to move is:
ΔX=L′−L=60cm−40cm=20cm
The jockey has to be moved by 20 cm to obtain balance when R is changed to 8Ω.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.50
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.51
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.48
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
The figure shows a metre-bridge circuit, with AB = 100 cm, x=24ΩandR=36Ω , and the jockey J in the position of balance
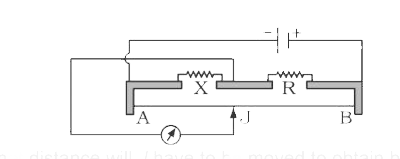
If R is now made 16Ω , through what distance will J have to be moved to obtain balance?
View Solution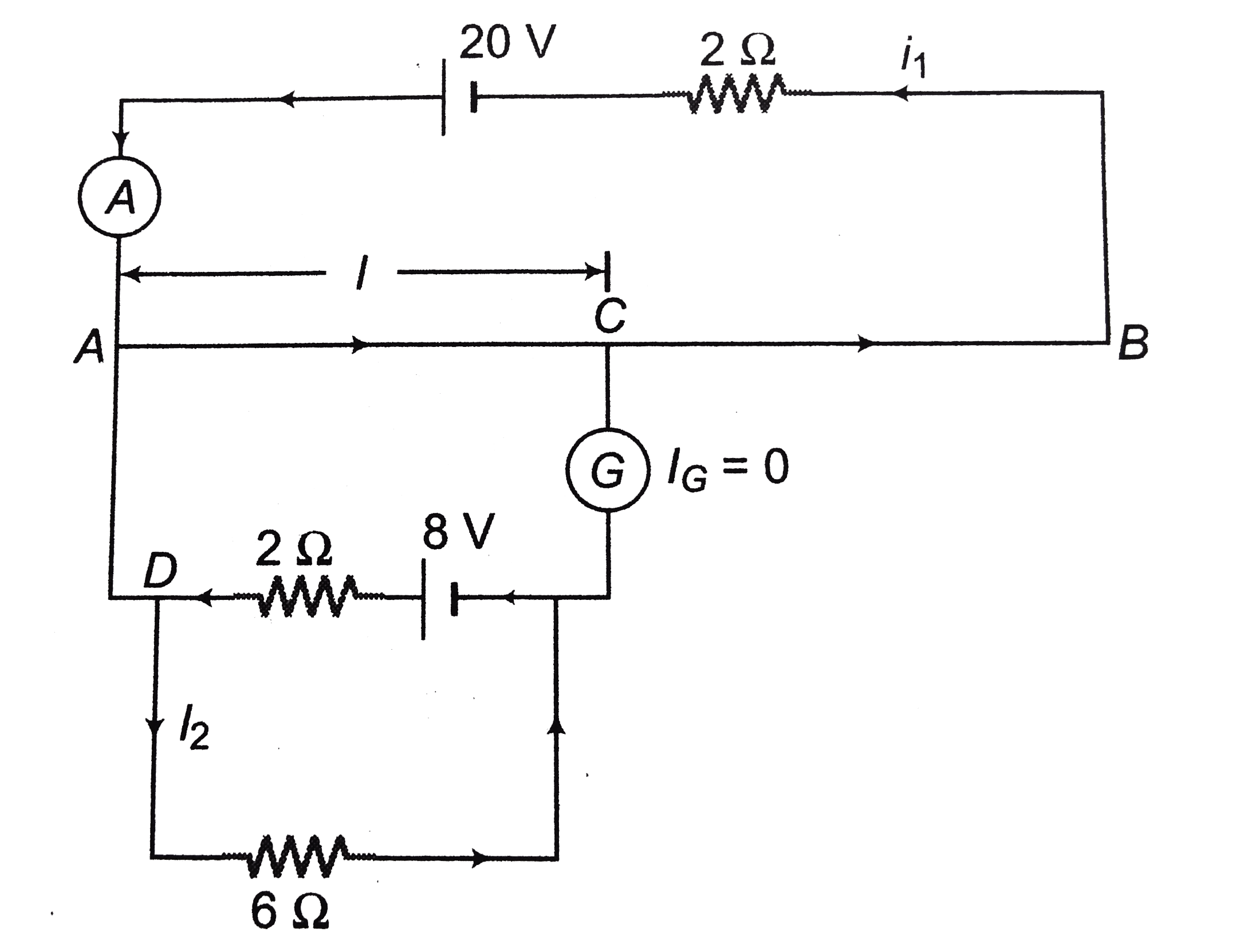
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.
View SolutionThe figure below shows a wheatstone bridge with resistors P and Q having almost equal resistance. When R = 400Ω , the bridge is in balanced condition. If on interchanging P and Q, the bridge is again balanced for R=405Ω, then the value of X is
View SolutionFigure shows a battery with emf 15 V in a circuit with R1=30Ω,R2=10Ω,R3=20Ω and capacitance C=10μF. The switch S is initially in the open position and is then closed at time t= 0. What will be the fimal steady - state charge on capacitor?

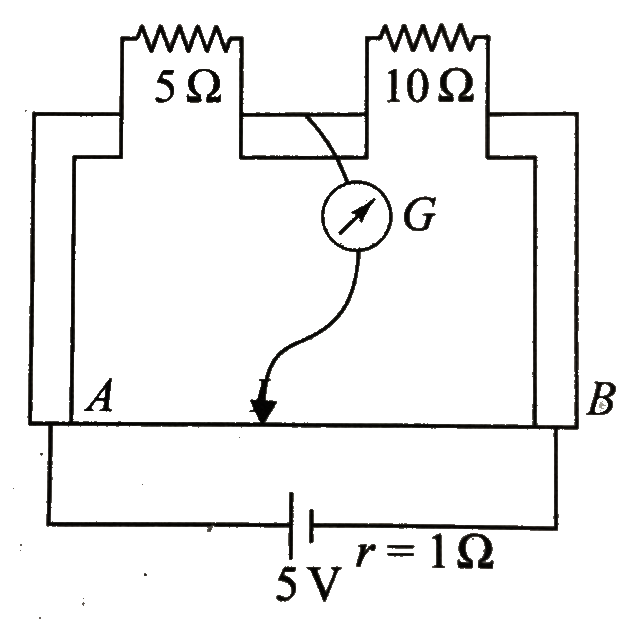
View SolutionIn a meter bridge circuit, the two resistances in the gap are 5Ω and 10Ω. The wire resistance is 4Ω. The emf of the cell connected at the ends of the wire is 5V and its internal resistance is 1Ω. What current will flow through the galvenometer of resistance 30Ω if the contact is made at the midpoint of wire ?
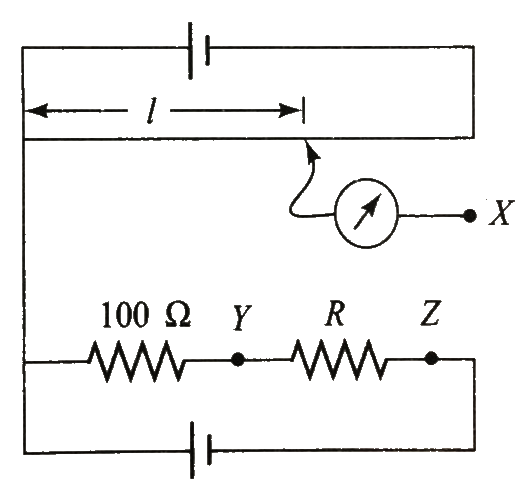
View SolutionFigure 6.49 shows a circuit that may be used to compare the resistance R of an unknown resistor with a 100Ω standard. The distance l from one end of the potentiometer slider wire to the balance point are 400mm and 588mm when X is connected to Y and Z, respectively. The length of the slide wire is 1.00m. What is the value of resistance R?
View Solution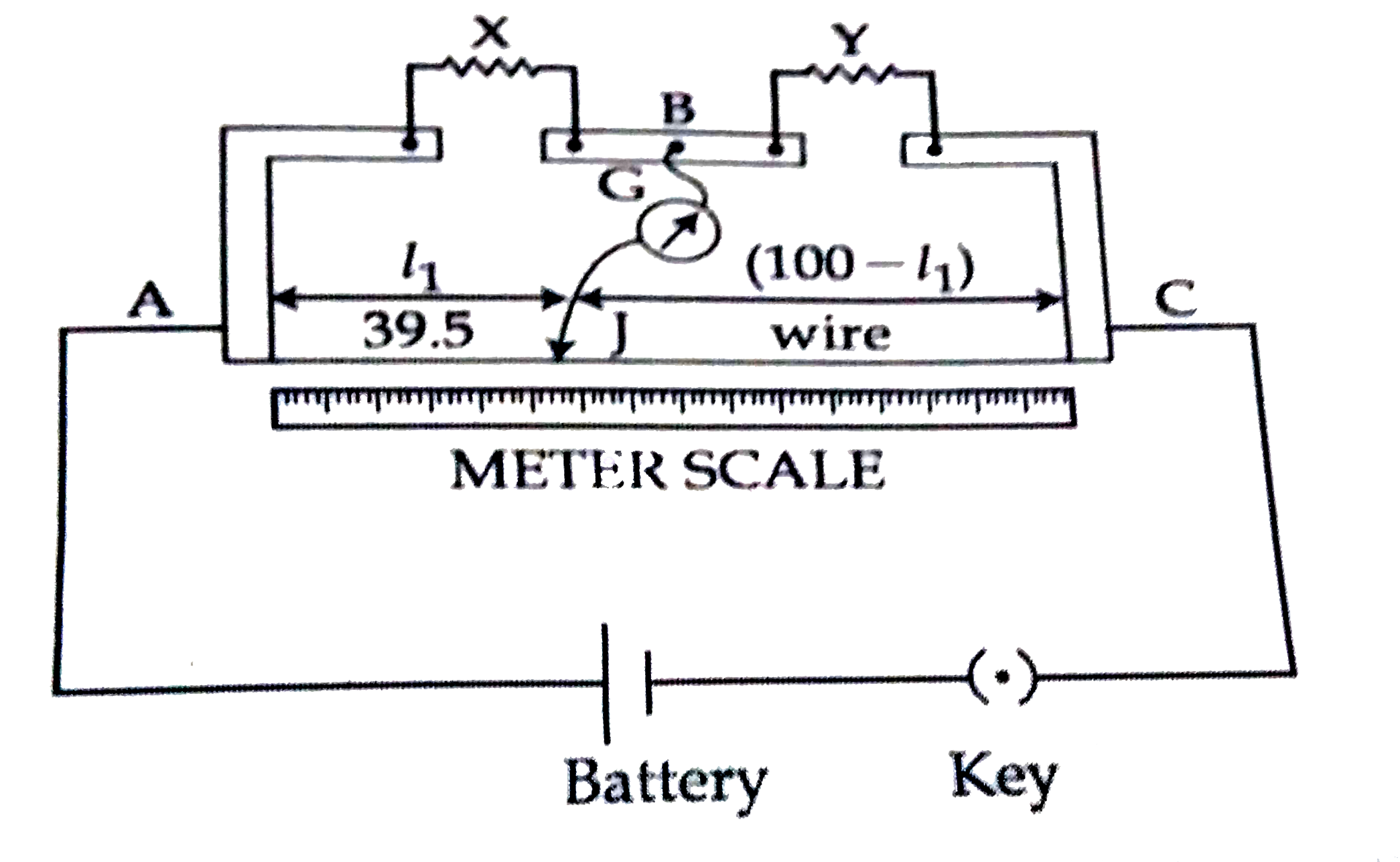
In a meter bridge, as shown in the figure, it is given that resistance Y=12.5Ω and that the balance is obtained at a distance 39.5cm from end A (by jockey J). After interchanging the resistance X and Y, a new balance point is found at a distance l2 from end A. What are the values of X and l2 ?
View SolutionThe figure shows a meter bridge wire AC having unifrom area o cross-section. X is a standard resistance of 4Ω and Y is a resistance coil. When Y is immersed in melting ice the null point is at 40 cm from point A. when the coil Y is heated to 100∘ C, a resistance of 100Ω has to be connected in parallel with Y, in order to kkep the bridge balanced at the sam point. The temperature coefficient of resistance of coil is
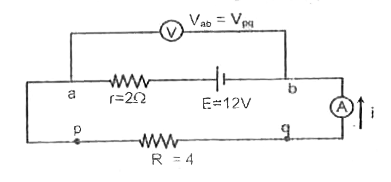
View SolutionThe figure shows a source (a battery) with an emf E of 12 V with an internal resistance r of 2Ω and an external resistance of 4Ω is added to complete the circuit. What are the voltmeter and ammeter readings
View SolutionThe figure
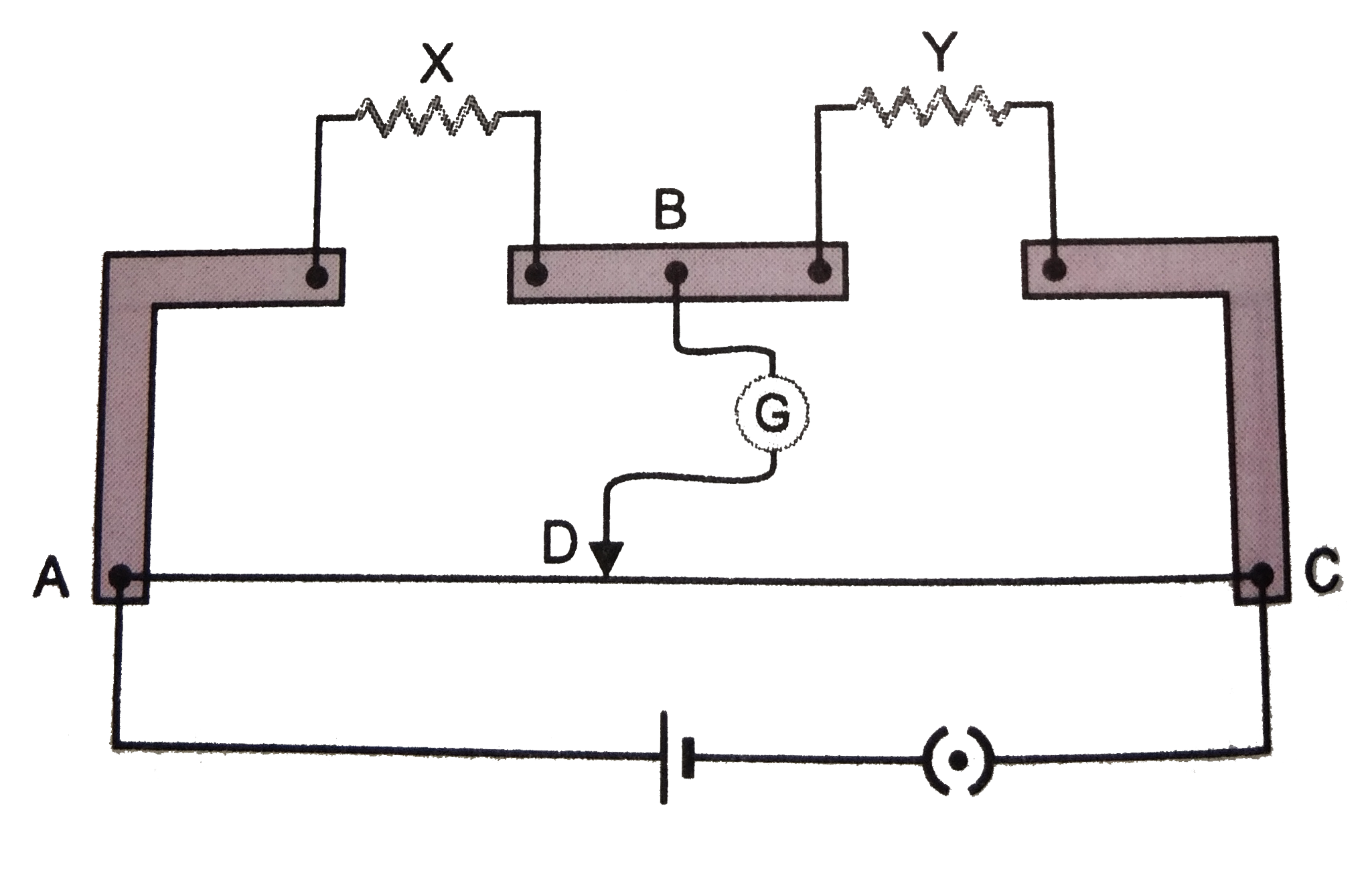
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.
View Solution
