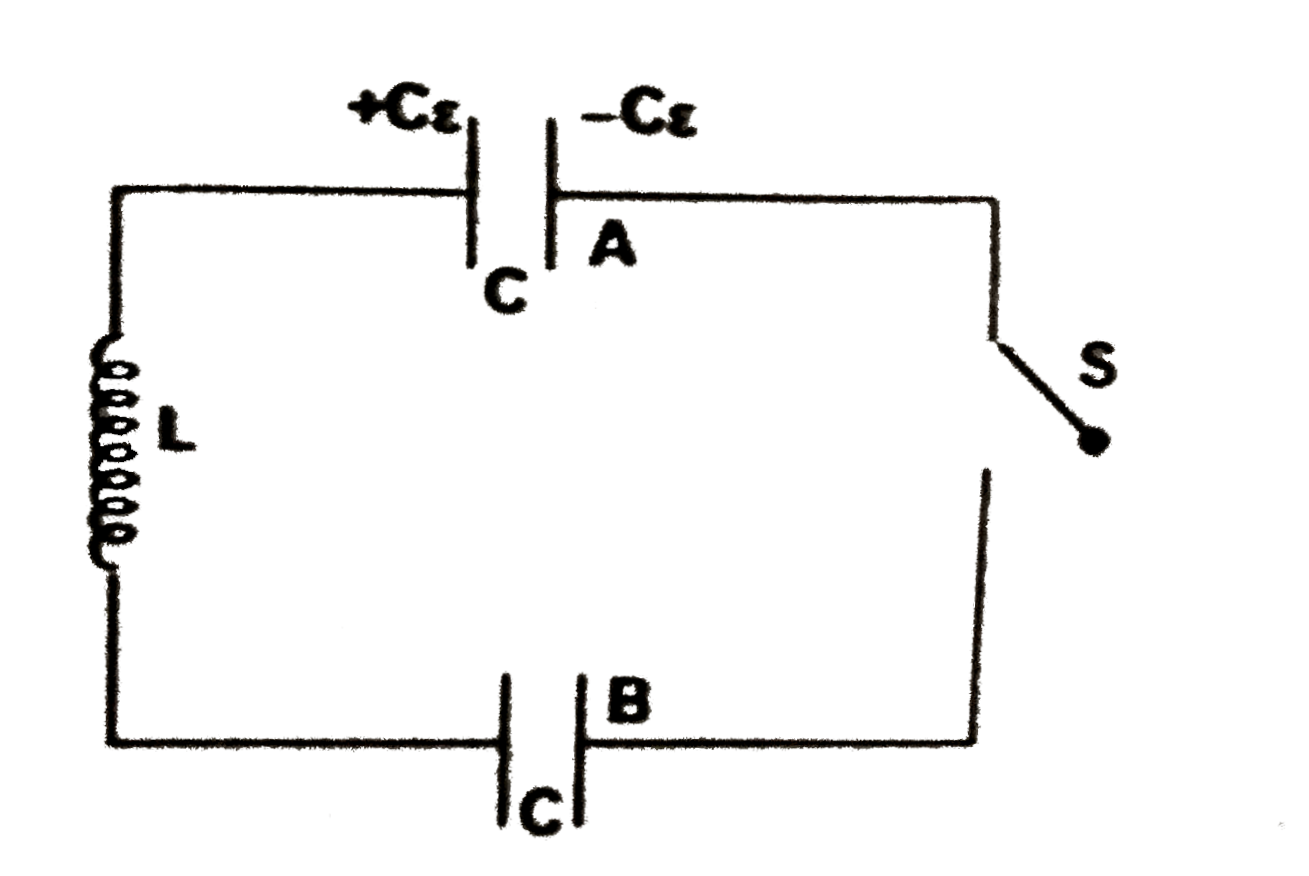
Initially capacitor 'A' is charged to a potential drop $ε$ and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is

$ε \sqrt{\frac{C}{2 L}}$

$ε \sqrt{\frac{C}{L}}$

$2 ε (\frac{C}{L})$

$\frac{ε}{2} \sqrt{\frac{C}{L}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

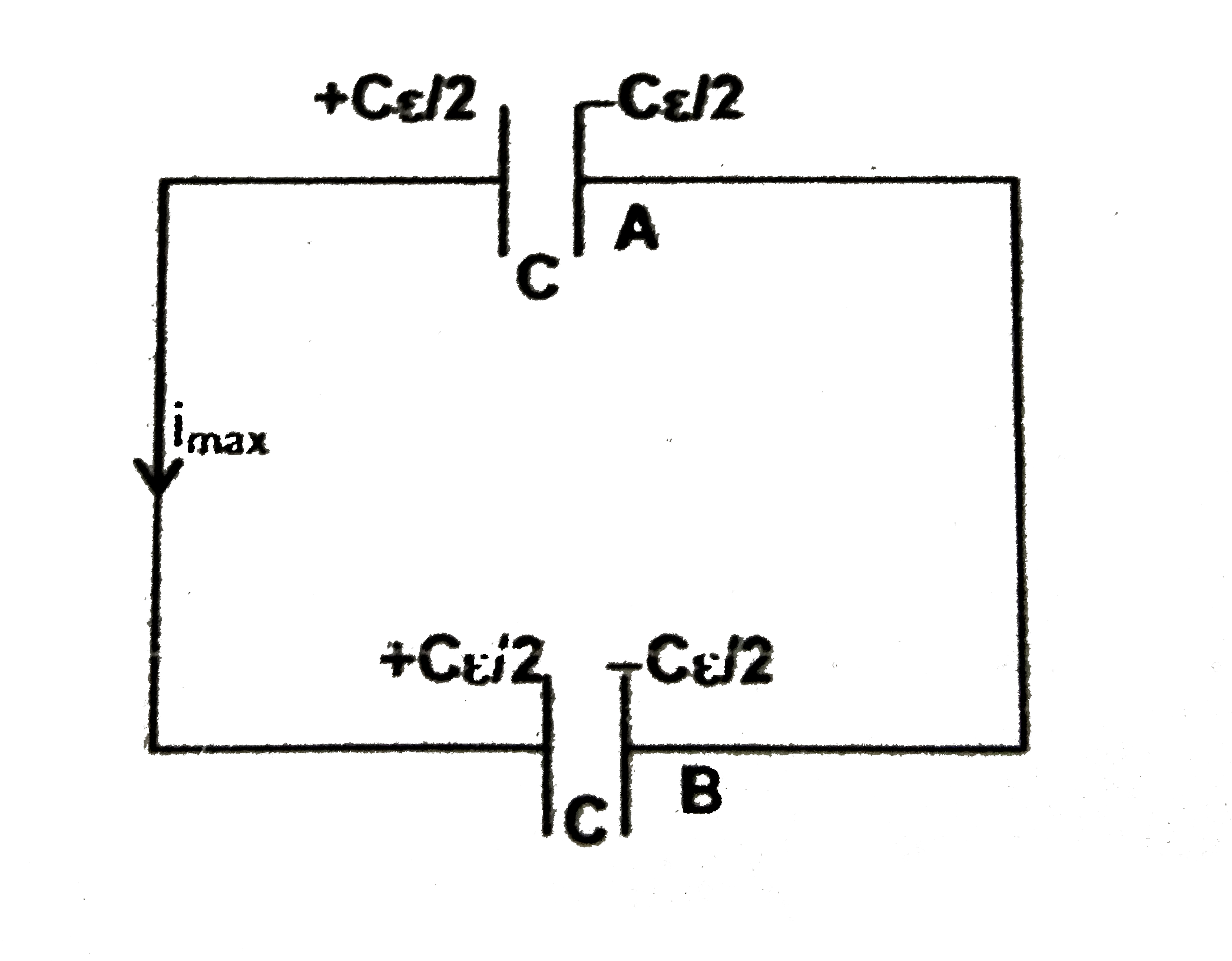
When the current through the inductor is maximum
$V_{L} = L \frac{d i}{d t} = 0$
Hence capacitors A and B will be in parallel now using conservation energy
$\frac{1}{2} C ε^{2} = 2 \times \frac{1}{2} C \frac{ε^{2}}{4} + \frac{1}{2} L i_{max}^{2}$
$\frac{C ε^{2}}{4} = \frac{1}{2} L i_{max}^{2}$
$i_{max} = ε \sqrt{\frac{C}{2 L}}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

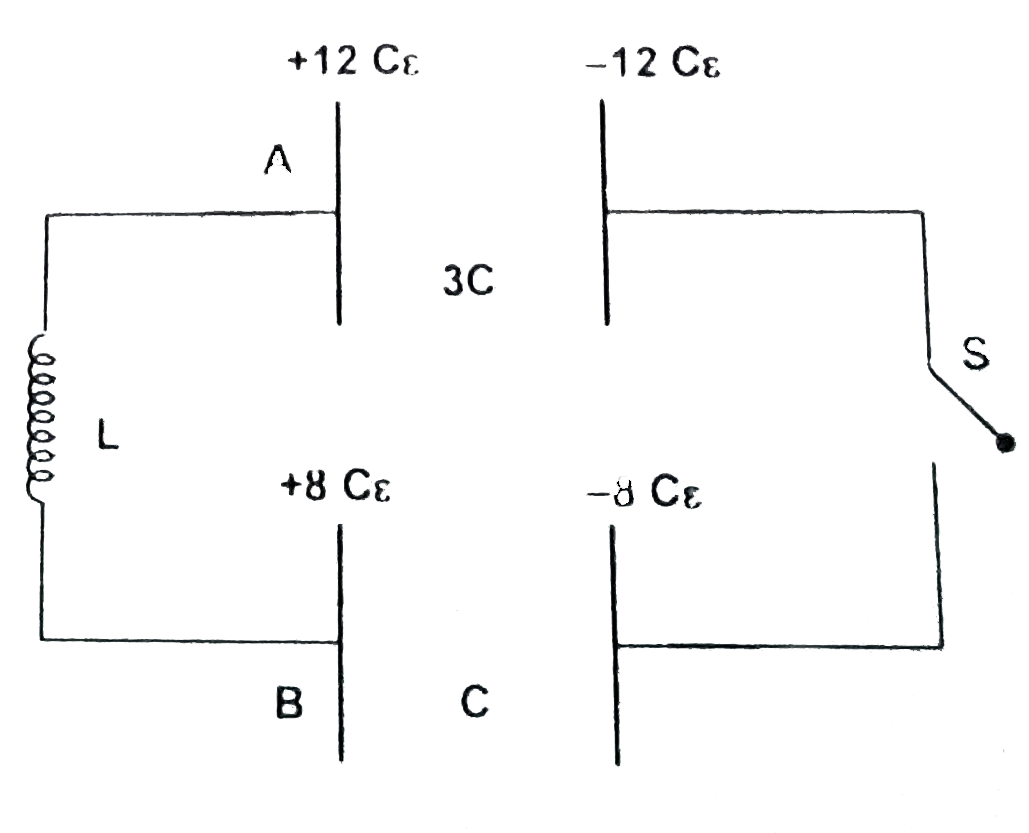
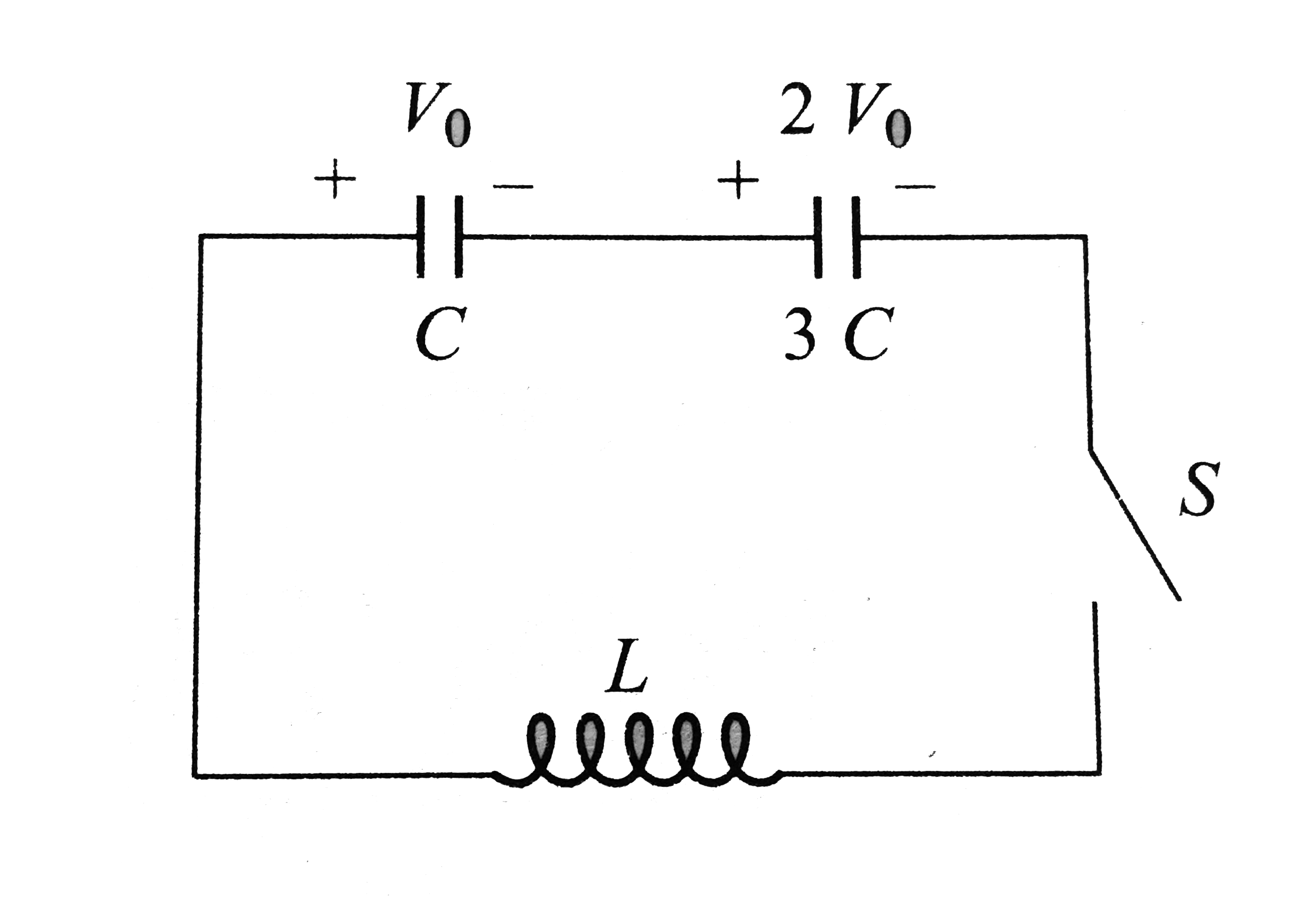
View Solution
In the adjacent circuit, the capacitor 'A' of capacitance '3C' and the capacitor 'B' of capacitance 'C' are initially charged by potential drops $4_{ɛ}$ and $8_{ɛ}$ respectively and connected through and inductor of inductance 'L' with zero initial current as shown. The switch 'S' is closed at $t = 0$ . then the maximum current through the inductor is

View Solution
A capacitor of capacitance Chas initial charge $Q_{0}$ and connected to an inductor L as shown. At $t = 0$ switch S is closed. The current through the inductor when energy in the capacitor is three times the energy of inductor is
View Solution
Initially the $900 μ F$ capacitor is charged to $100 V$ and the $100 μ F$ capacitor is uncharged in Fig. Then switch $S_{2}$ is closed for time $t_{1}$ , after which it is opened and at the same instant switch $S_{1}$ is closed for time $t_{2}$ and then opened. It is now found that $100 μ F$ capacitor is charged to $300 μ F$ capacitor is charged to $300 V$ . Find the minimum possible value of the time interval $t_{1}$ and $t_{2}$ .

View Solution
In the circuit shown, switch $S$ is closed at time $t = 0$ . Find the current through the inductor as a function of time $t$ .

View Solution
Initially capacitor is uncharged at $t = 0$ switch is closed. Charge on capacitor when current in the circuit is $10 %$ of maximum current :

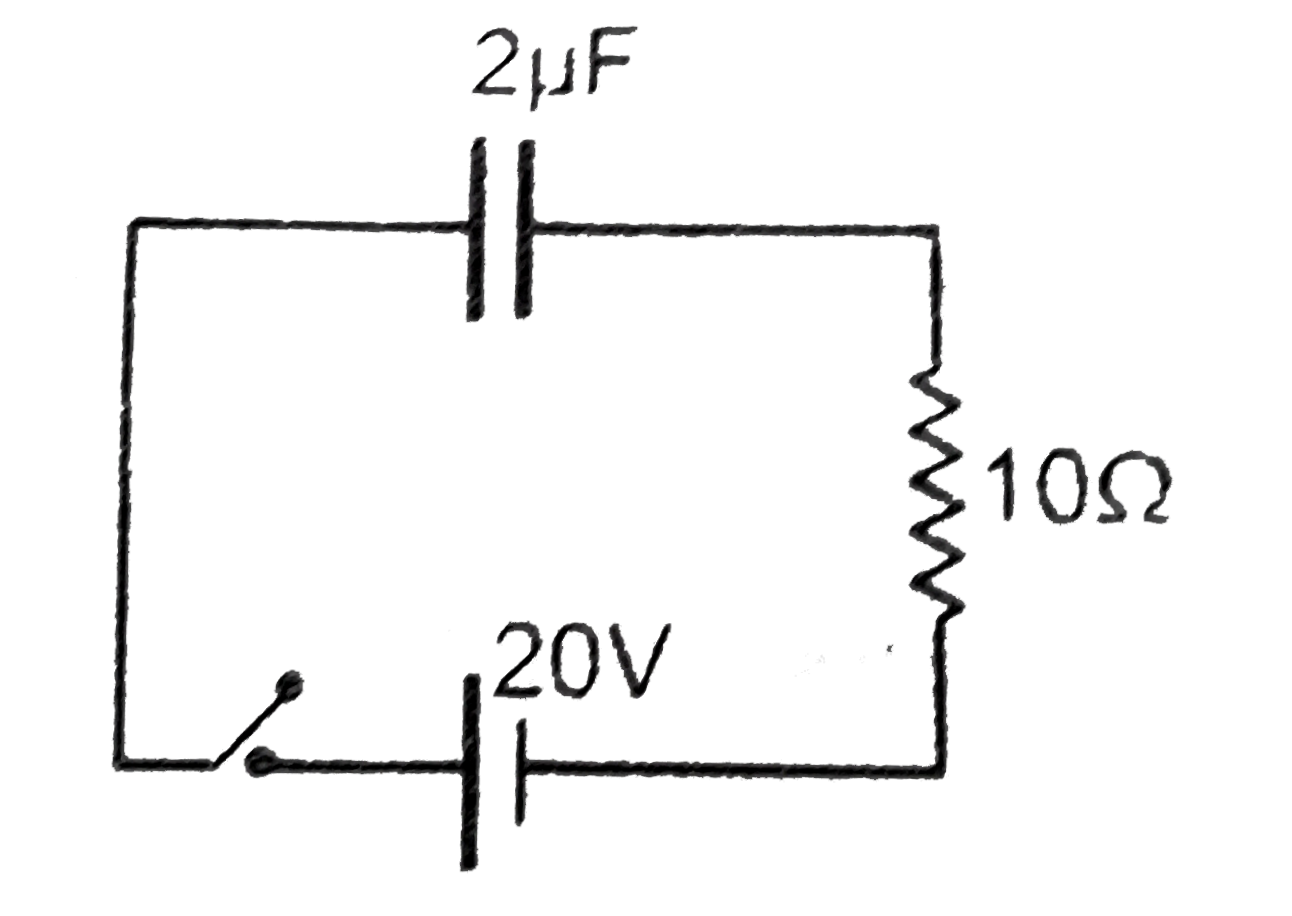
View Solution
For the circuit shown in figure below, at t = 0, switch is closed, the initial current through resistor and final charge on capacitor are

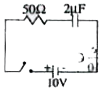
View Solution
Two capacitors of capacitance $C$ and $3 C$ are charged to potential difference $V_{0}$ and $2 V_{0}$ , respectively, and connected to an inductor of inductance $L$ as shows in Fig. Initially, the current in the inductor is zero. Now, switch $S$ is closed.

The maximum current in the inductor is
View Solution
there in no current part of this circuit for time $t < o$ . Switch $S$ is closed at $t = 0$ .

The rate at which the current through the inductor increases initially is
View Solution
Initially the $900 μ F$ capacitor is charged to 100 V and the $100 μ F$ capacitor is uncharged in the figure shown. Then the switch $S_{2}$ is closed for a time $t_{1}$ , after which it is opened and at the same instant switch $S_{1}$ is closed for a time $t_{2}$ and then opened. It is now found that the $100 μ F$ capacitor is charged to 300 V. If $t_{1} and t_{2}$ minimum possible values of the time intervals, then findout $\frac{t_{1}}{t_{2}}$

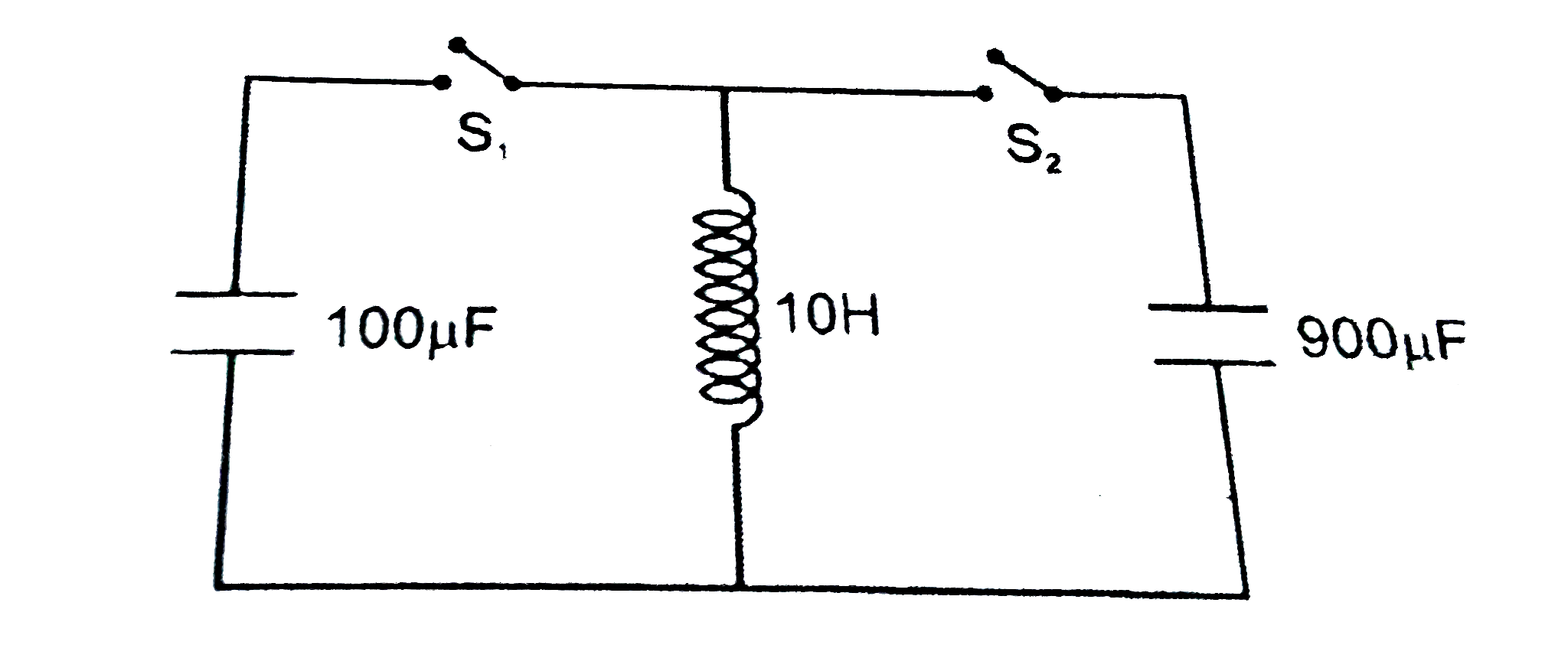
View Solution

Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is

The correct Answer is:A

When the current through the inductor is maximum VL=Ldidt=0 Hence capacitors A and B will be in parallel now using conservation energy 12Cε2=2×12Cε24+12Li2max Cε24=12Li2max imax=ε√C2L

Similar Questions

Recommended Questions

Initially capacitor 'A' is charged to a potential drop $ε$ and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is