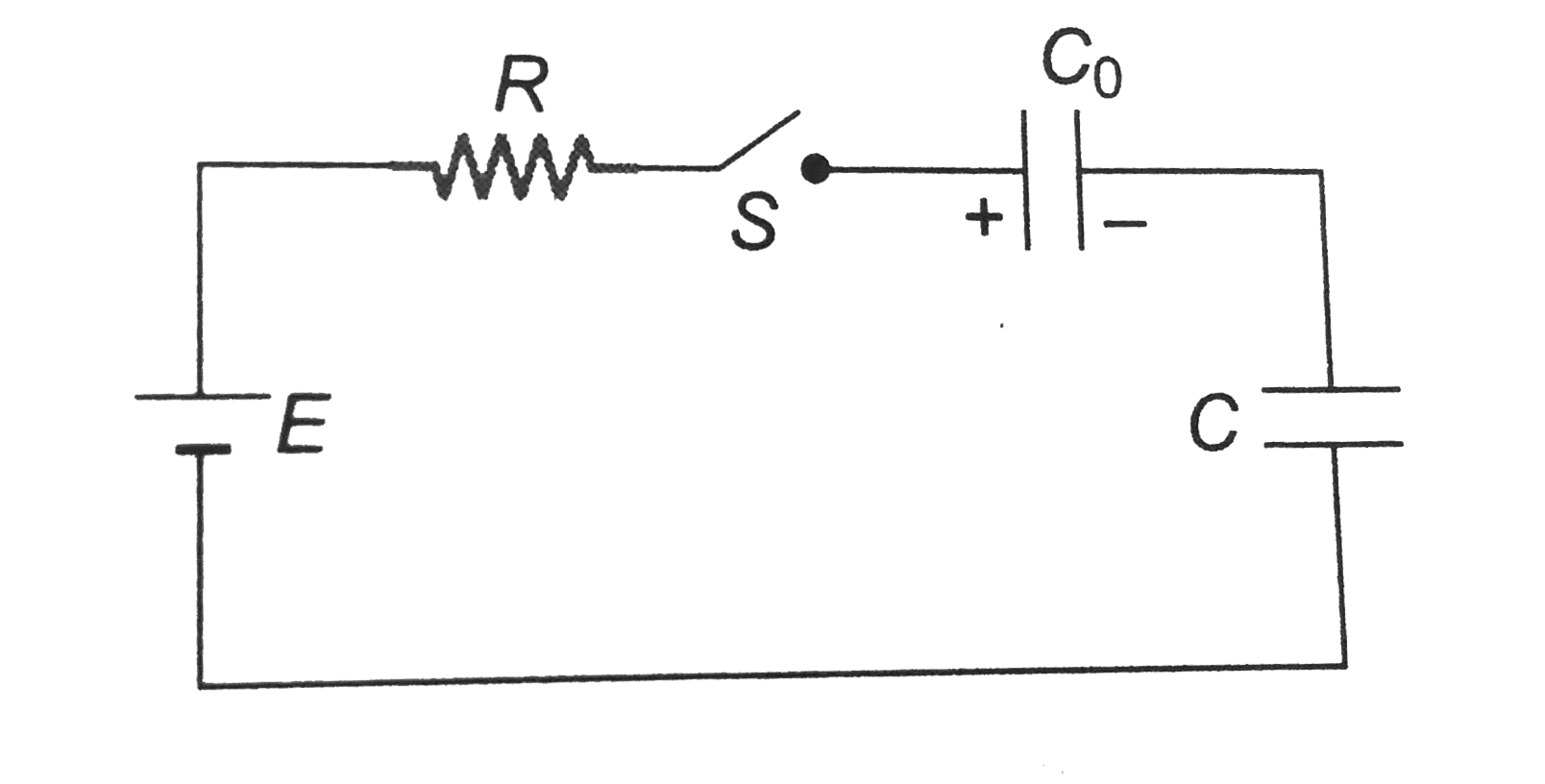
The switch S is closed aty t = 0. the capacitor C is uncharged but C0 has a charge q0 at t =0. Calculate the current i(t) in the circuit
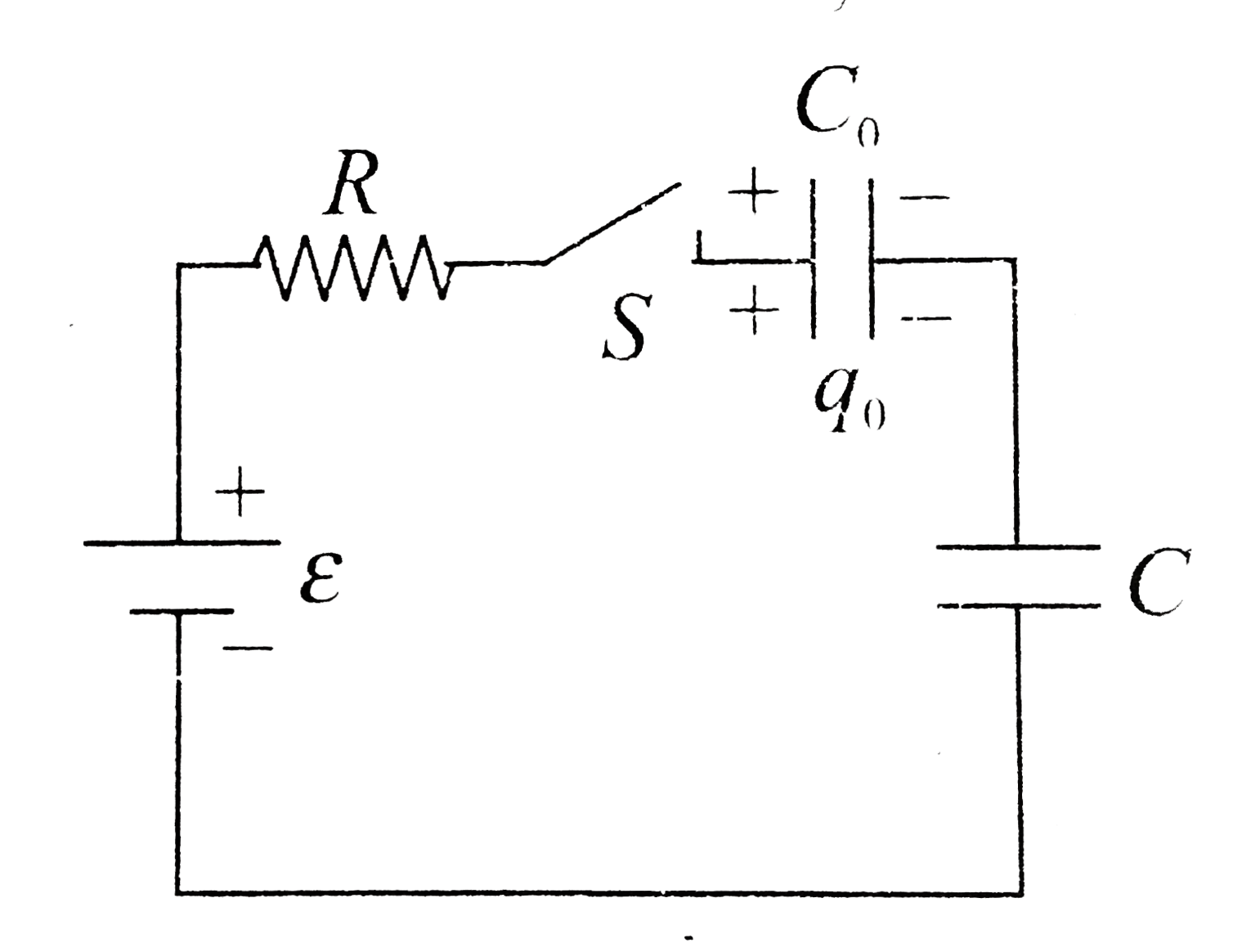
Let q0 and q be the instantaneous charges on C0 and C, respectively. Applying KVL to the circuit, we have
q0C0+qC+iR=ε
Differentiating this equation, we get
1C0dq0dt+1Cdqdt+Rdidt=0
or i⎡⎣1C0+1C=Rdidtori[C+C0CC0]=−Rdidt
(wherei=dq0dt)=dqdt
or Intergrating this expression, we have
∫i(t)i0dti=∫t0dtRCeqor[logei]i(t)i0=−tRCeq
or i(t)=i0e−(t/R)Ceq
where i0 is the inital current.
Further, i0R+q0C0=εori0=(E−eq0C0)/R (iii)
Substituting i0 form Eq. (iii) into Eq. (ii)we get
i(t)=[E−(q0/C0)R]e−(tRCeq), where Ceq=CC0(C+C0)
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Single Correct
Explore 72 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Multiple Correct
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.2
Explore 50 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check
In the circuit shown key is closed at t=0 with capacitor initially uncharged.
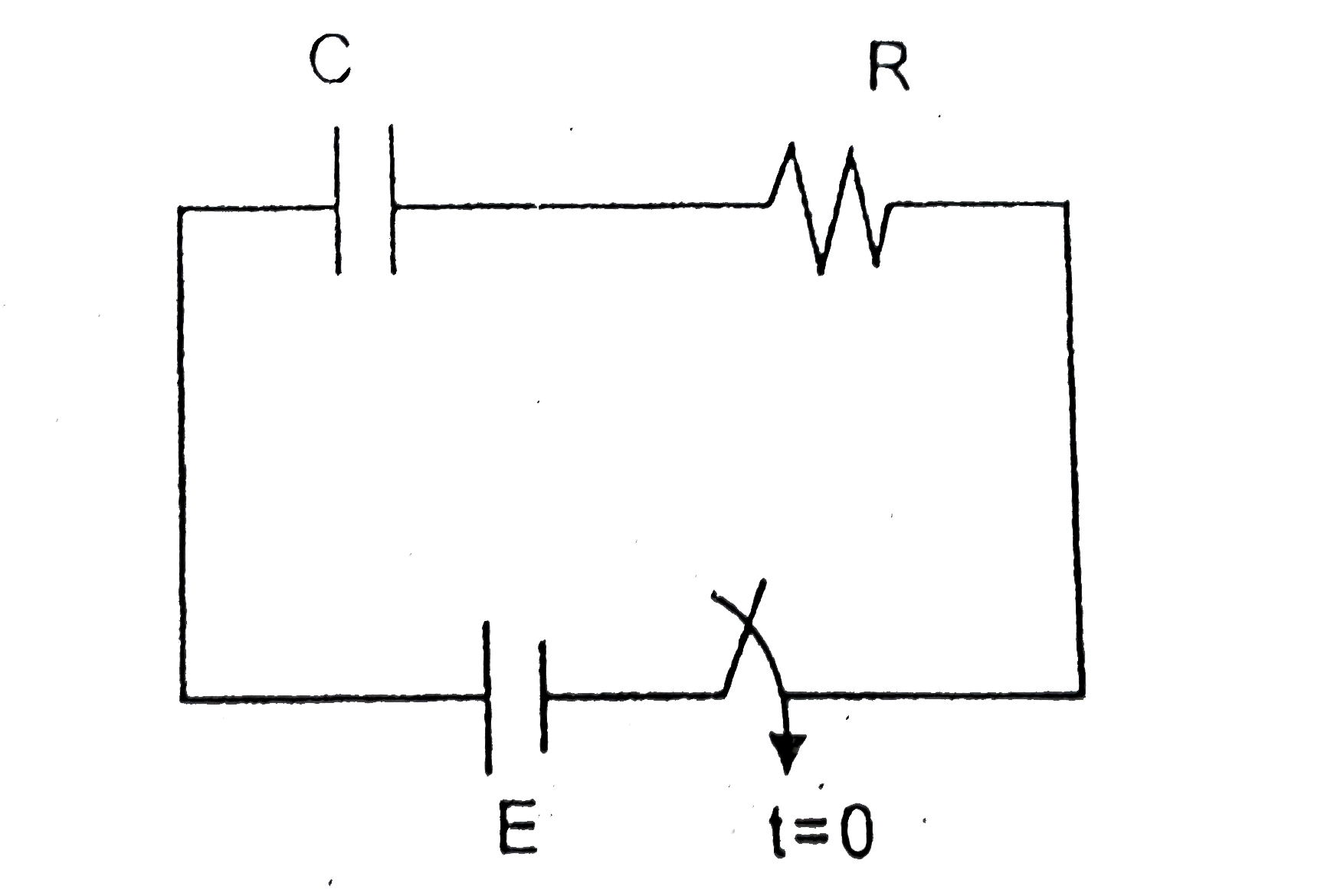 ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.
ARate of increase of capacitors energy, just after the switch is closed is E2RBMaximum power supplied by the cell is E2RCAt t=RCIn2, capacitor is charged up to half of the energy stored by it in steady stateDAt t=RCIn2, potential difference across capacitor is same that across resistor.Two plates of a charged capacitor are connected to each through a resistance and a switch which is kept open initially. The switch is closed at t= 0. If q is charge on capacitor and I is the current in the circuit at time t then the curves that correctly represent the variation of the change and current with time are:
A B
B C
C D
D
Initially capacitor is uncharged at t=0 switch is closed. Charge on capacitor when current in the circuit is 10% of maximum current :
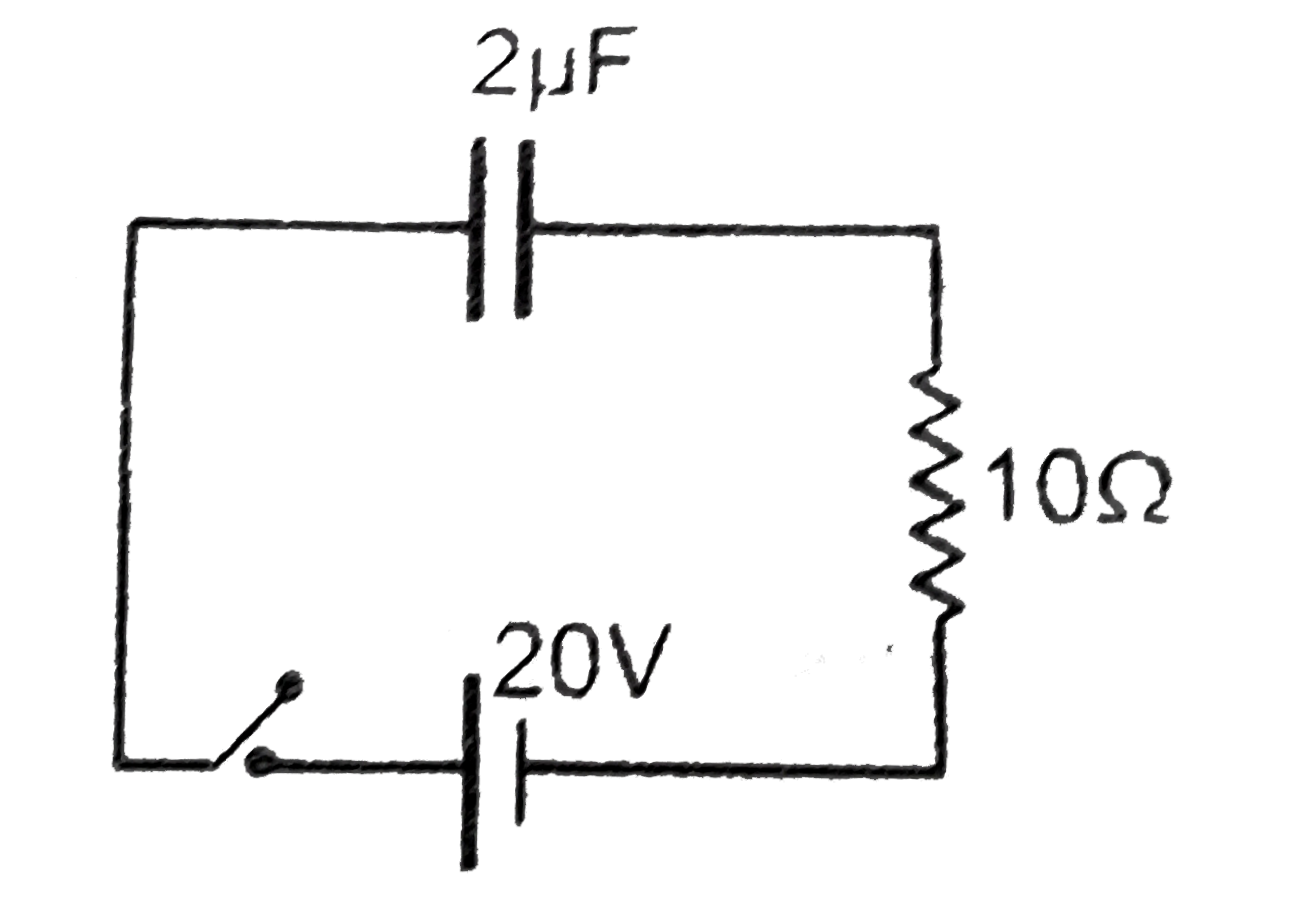 A4μCB8μCC36μCD16μC
A4μCB8μCC36μCD16μC
For the arrangement shown in the figure, the switch is closed at t=0. C2 is initially uncharged while C1 has a charge of 2μC
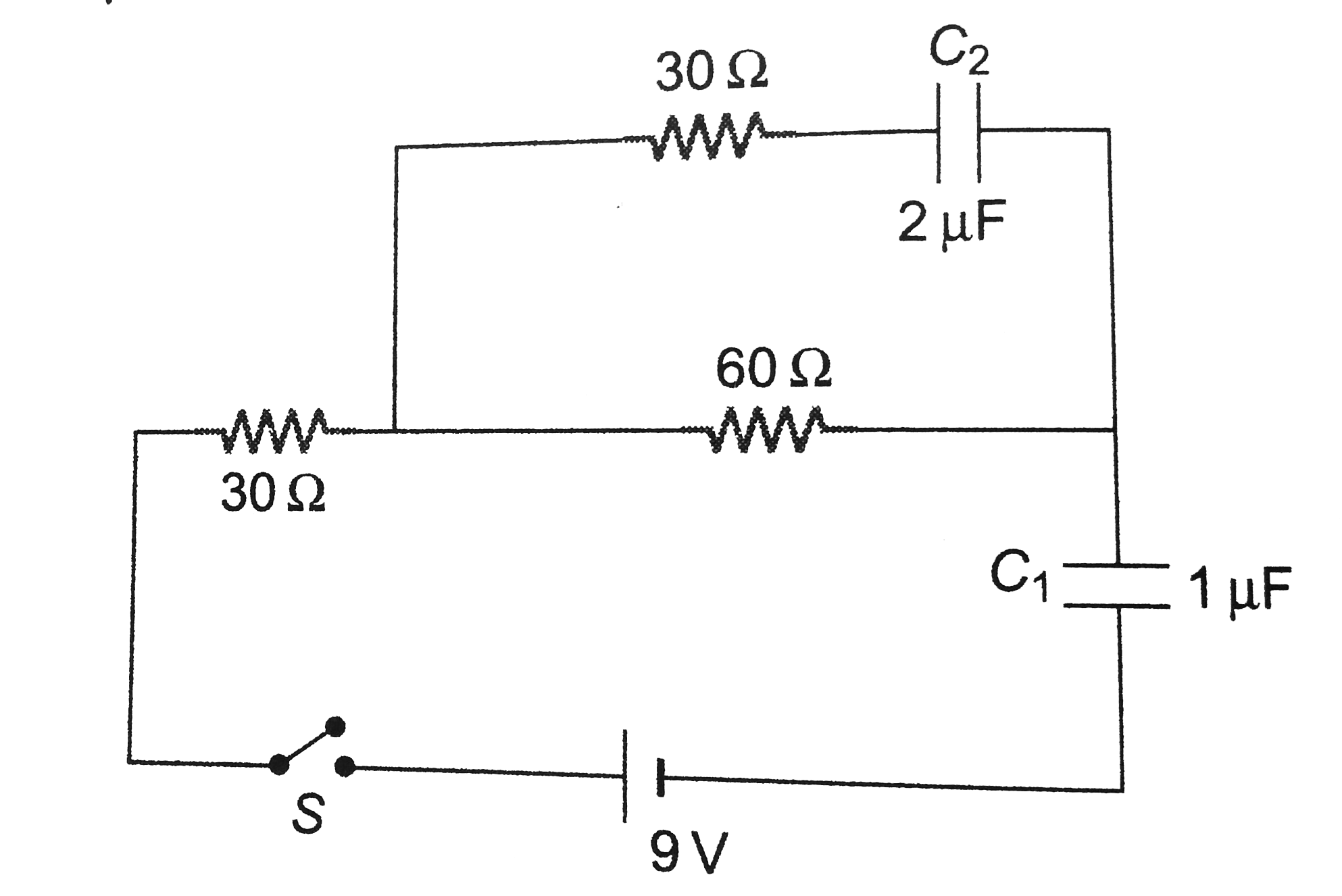
(a) Find the current comingn out of the battery just after the switch is closed.
(b) Find the charge on the capacitors in the steady state condition.
View SolutionIn the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
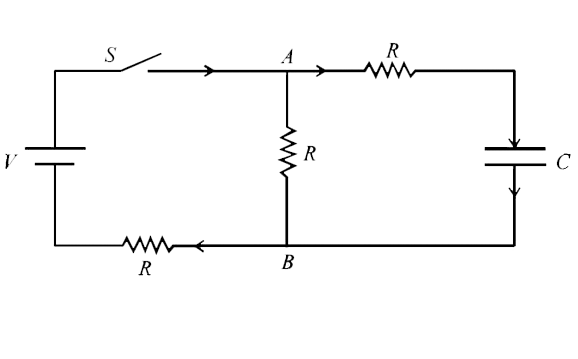 .
.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then capacitor is initially uncharged. Then the current through the resistor R=8Ω at t=0.4×10−3sec is (Take e−2=0.135 )

View Solution
In given LR circuit the switch S is closed at time t=0 then
View Solution
_PHY_E06_157_Q01.png)