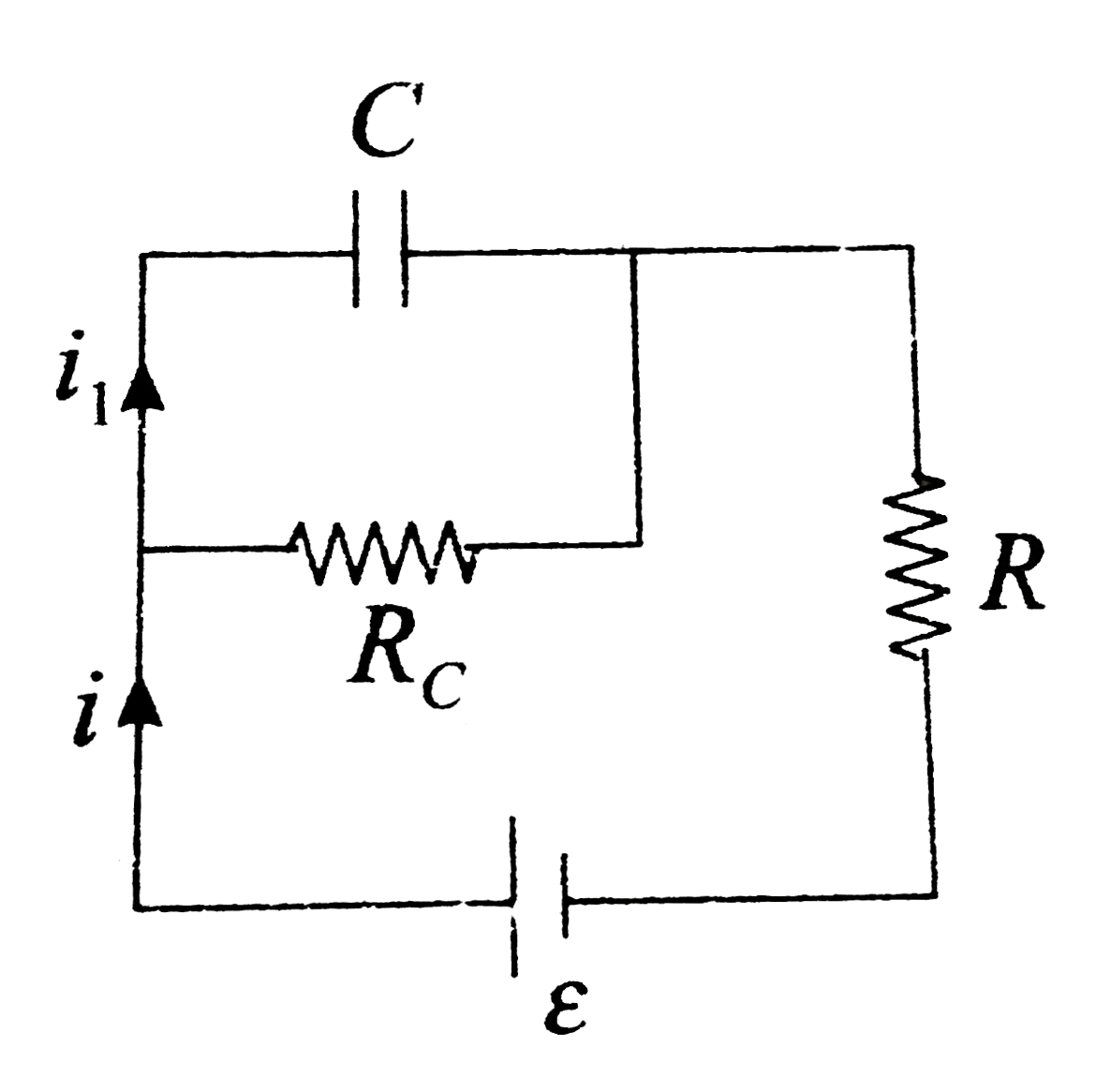
Consider a parallel pate capacitor of capactance C with partially conducting medium between its plates having a resistacne Rc if this capacitor is connected to a battery of emf ε and a resistor R as shown in fig.
a. charge on the capacitor as a function of time.
The switch R as a function of time.

The equivalent circuit can be drawn as shown. Applying
Kirchhoff's law for the two loops,
(i−i1)RC+iR=ε (i)
qC=RC(i=i1) (ii)
Eliminating I between (i) and (ii) we get
qC=(1+RRC)+i1R=ε
For capacitor C,dqdt=i1
dqdt=CE−q(1+α)RC(whereα=RC)
Solving, we get
q=EC1+α(1−e−t(1+α)/RC)
Adding (i) and (ii), we get
QC+iR=Eori=CE−qRC
Substituting for q, we get
I=ER[1−11+α(1−e−t(1+α)RC)](whereα=RRC)
Topper's Solved these Questions
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Single Correct
Explore 72 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Multiple Correct
Explore 16 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Exercise 5.2
Explore 50 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
Similar Questions
Knowledge Check
Figure shows a LCR circuit connected with a battery emf ε and internal resistance 'R'. After a long time (initially the capacitor was uncharged)
 ACurrent through the inductor is ε8RBCharge stored in the capacitor is Cε4CCharge stored in the capacitor is Cε2DPotential difference across the terminals of battery is ε4
ACurrent through the inductor is ε8RBCharge stored in the capacitor is Cε4CCharge stored in the capacitor is Cε2DPotential difference across the terminals of battery is ε4A parallel plate capacitor has a capacity c. If a medium of dielectric constant K is introduced between plates, the capacity of capacitor becomes
ACKBCK2CK2CDKC
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionConsider the situation shown in figure.The switch is closed at t=0when the capacitor C1as a function of time t.
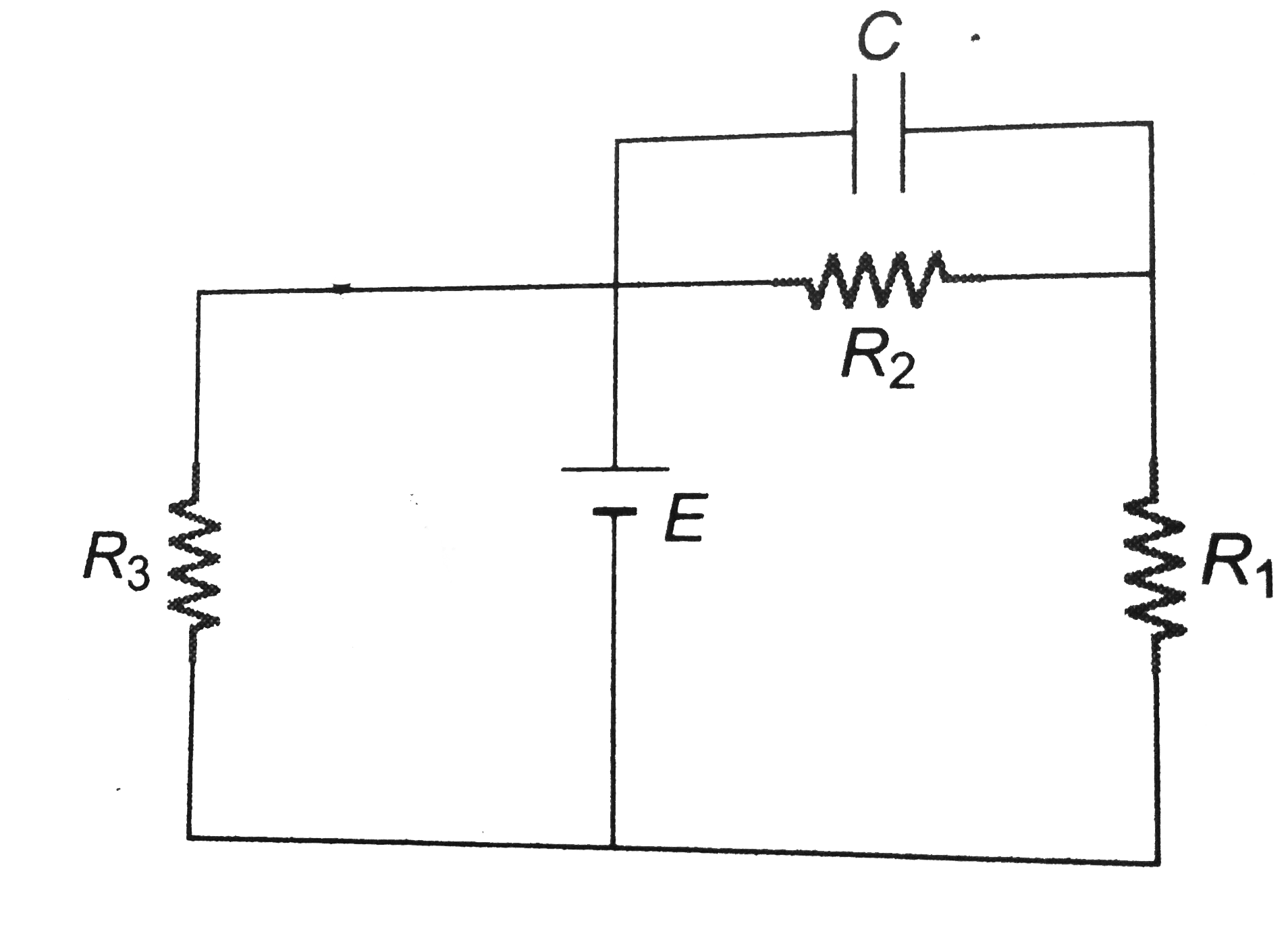
View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
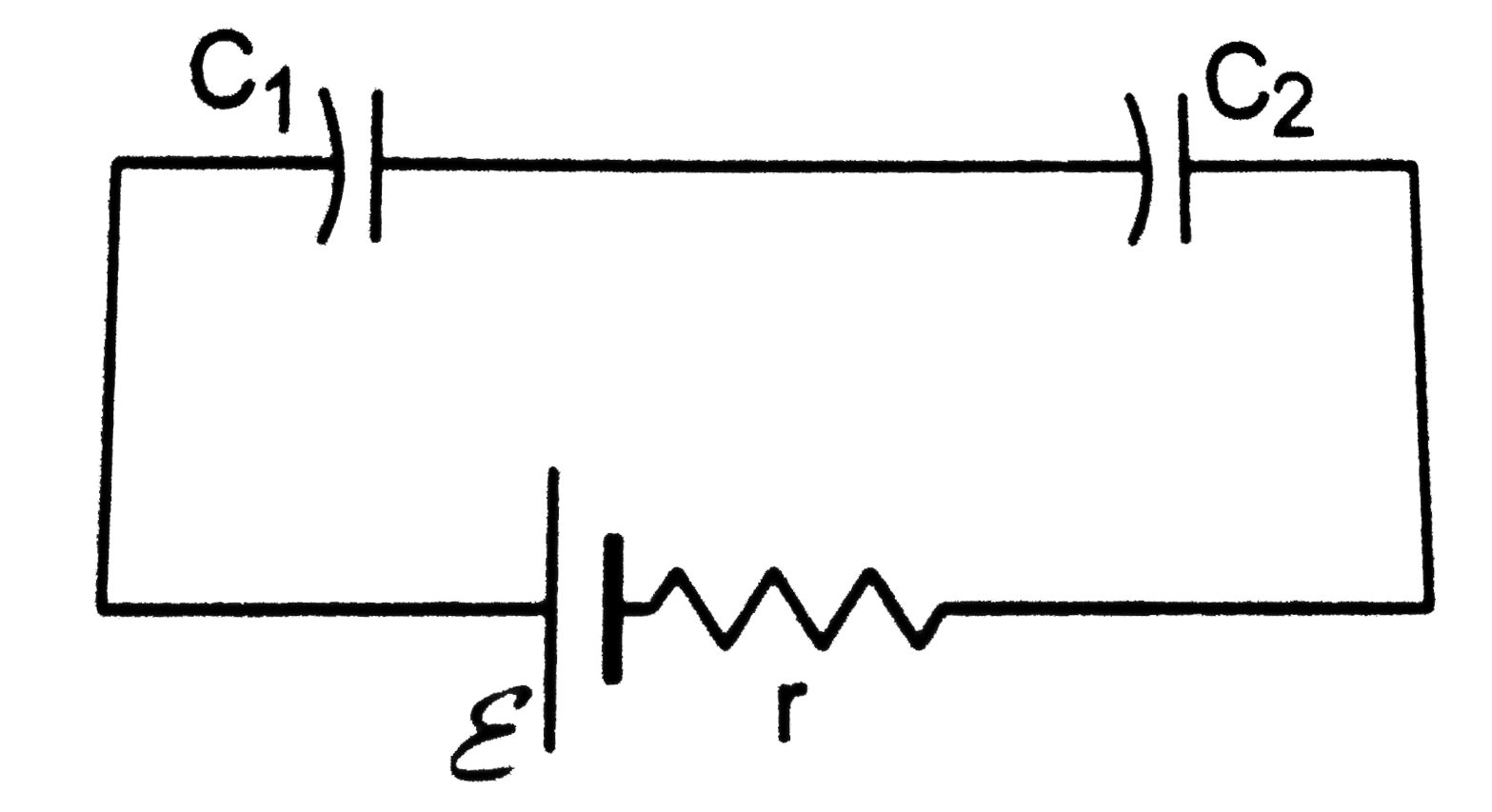
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View Solution