Two particles of combined mass M, placed in space with certain separation are released interaction between the particles is only of gravitational nature and there is no external force present. Acceleration of one particle with respect to the other when separation between them is R, has a magnitude :
GM2R2
GMR2
2GMR2
not possible to calculate due to lack of information
The correct Answer is:B
To solve the problem, we need to find the acceleration of one particle with respect to the other when they are separated by a distance R and only gravitational forces are acting between them.
1. Understanding the Forces:
- Let the two particles have masses M1 and M2.
- The gravitational force F between them is given by Newton's law of gravitation:
F=GM1M2R2
- Here, G is the gravitational constant, and R is the separation between the two particles.
2. Finding Acceleration of Each Particle:
- The acceleration a1 of particle M1 due to the gravitational force exerted by M2 is given by:
F=M1a1⟹a1=FM1=GM2R2
- Similarly, the acceleration a2 of particle M2 due to the gravitational force exerted by M1 is:
F=M2a2⟹a2=FM2=GM1R2
3. Relative Acceleration:
- The relative acceleration A of one particle with respect to the other is the sum of their individual accelerations since they are moving towards each other:
A=a1+a2=GM2R2+GM1R2
- This can be simplified to:
A=G(M1+M2)R2
4. Using Combined Mass:
- Given that the combined mass M=M1+M2, we can substitute this into our equation:
A=GMR2
5. Final Result:
- Therefore, the magnitude of the acceleration of one particle with respect to the other when the separation between them is R is:
A=GMR2
- Let the two particles have masses M1 and M2.
- The gravitational force F between them is given by Newton's law of gravitation:
F=GM1M2R2
- Here, G is the gravitational constant, and R is the separation between the two particles.
- The acceleration a1 of particle M1 due to the gravitational force exerted by M2 is given by:
F=M1a1⟹a1=FM1=GM2R2
- Similarly, the acceleration a2 of particle M2 due to the gravitational force exerted by M1 is:
F=M2a2⟹a2=FM2=GM1R2
- The relative acceleration A of one particle with respect to the other is the sum of their individual accelerations since they are moving towards each other:
A=a1+a2=GM2R2+GM1R2
- This can be simplified to:
A=G(M1+M2)R2
- Given that the combined mass M=M1+M2, we can substitute this into our equation:
A=GMR2
- Therefore, the magnitude of the acceleration of one particle with respect to the other when the separation between them is R is:
A=GMR2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.37
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.38
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.35
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
How is the gravitational force between two masses affected if the separation between them is doubled ?
View SolutionTwo particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only forces acting on the particles are their mutual gravitation find the initial acceleration of the two particles.
View Solution
Knowledge Check
If the distance between two point particles is doubled, then the gravitational force between them
Adecreases by a factor of 4Bdecreases by a factor of 2Cincreases by a factor of 2Dincreases by a factor of 4
Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only forces acting on the particles are their mutual gravitation find the initial acceleration of the two particles.
View SolutionHow is the gravitational force between two point masses affected when they are dipped in water keeping the separation between them the same ?
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,
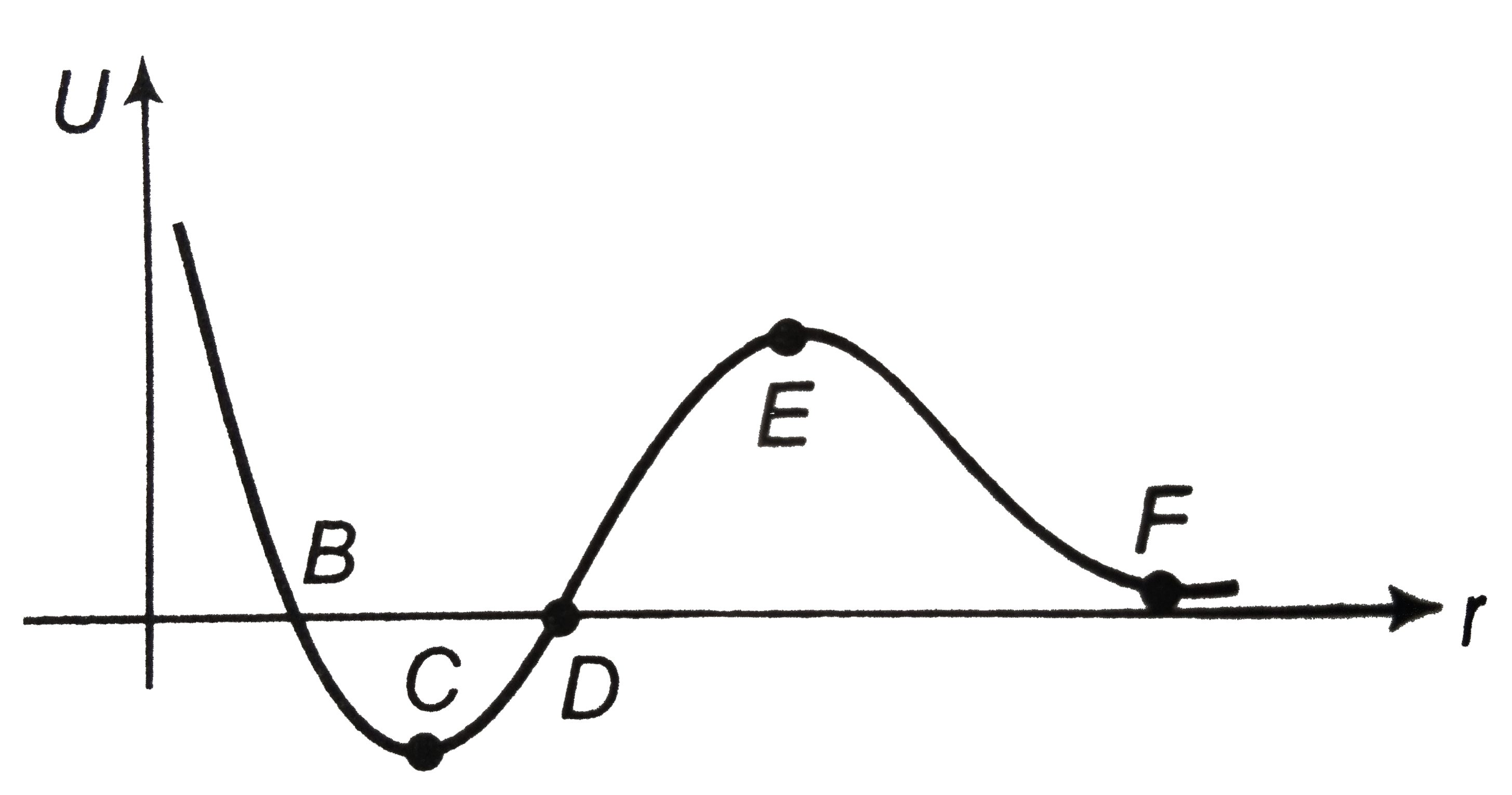
View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
View SolutionThe separation between two masses is reduced to half. How is the magnitude of gravitational force between them affected ?
View SolutionConsider a system of two identical particles. One of the particles is at rest and the other has an acceleration. The centre of mass has an acceleration.
View Solution
