A square surface of side L metre is in the plane of the paper. A uniform electric field E (volt/m), also in the plane of the paper, is limited only to the lower half of the square surface, (see figure). The electric flux in SI units associated with the surface is

EL2/(2ε0)
EL2/2
zero
EL2
The correct Answer is:C
Electric flux (ϕe) is a measure of the number of field lines crossing a surface. The numgber of filled lines passing through unit are (N/S) will be proportional to the electric field, or
NS∝E⇒N∝ES
The quantity ES is the electric flux through surface S.
As we have seen in the problem that, lines of force that enter the closed surface leave the surface immediately, so no electric flux is blund to the system. Hence, electric flux is zero.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.37
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.38
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.35
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A square surface of side Lm is in the plane of the paper. A uniform electric field →E(V/m), also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in SI units associated with the surface is:

View SolutionA square surface of side L meter in the plane of the paper is placed in a uniform electric field E (volt/m) acting along the same plane at an angle θ with the horizontal side of the square as shown in figure. The electric flux linked to the surface, in units of volt-m, is –

View SolutionA square surface of side L metre in the plane of the paper is placed in a uniform electric field E(volt/m) acting along the same place at an anlge θ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of V−m is
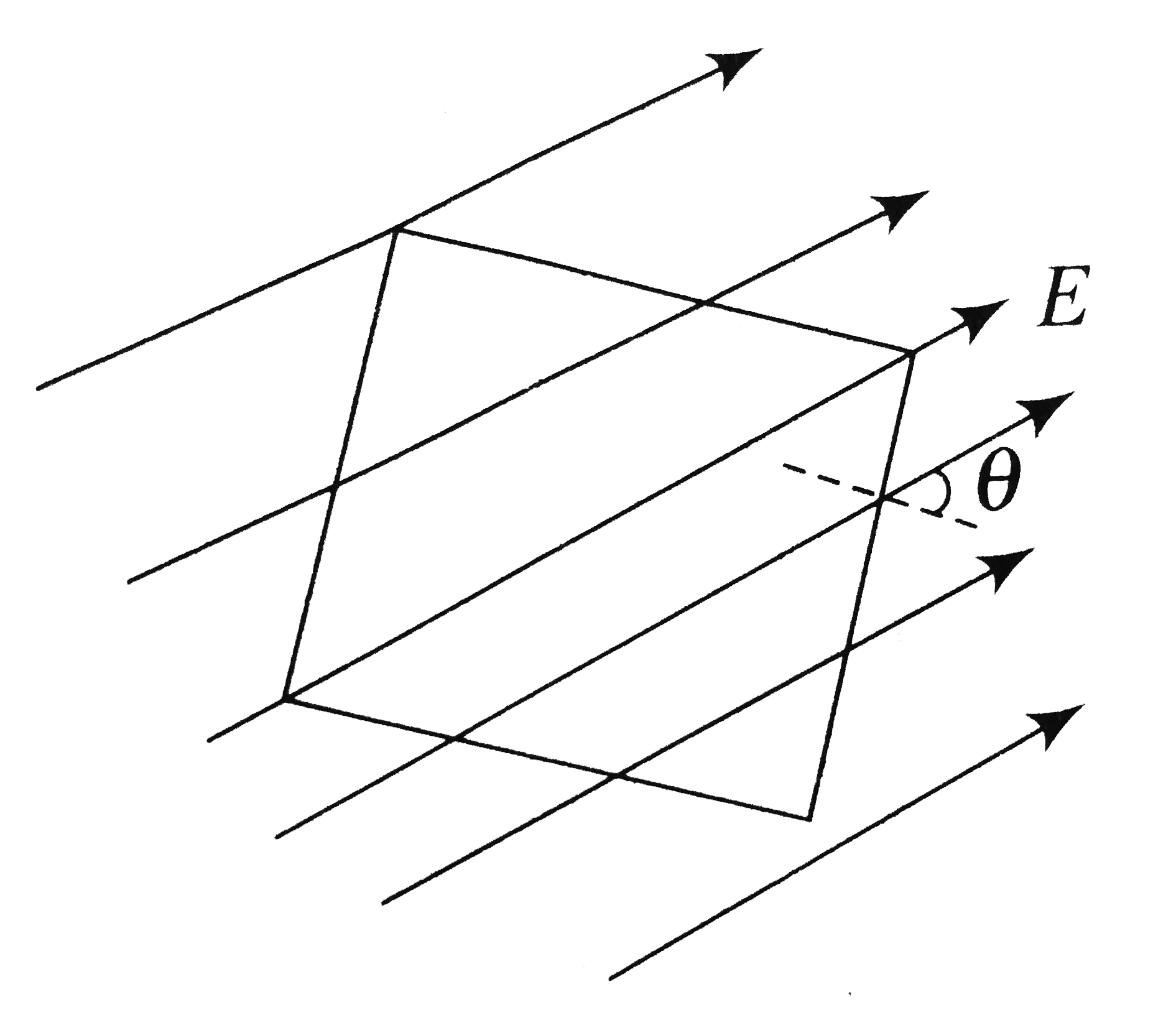
View SolutionA square surface of side L metre in the plane of the paper is placed in a uniform electric field E(volt/m) acting along the same place at an anlge θ with the horizontal side of the square as shown in figure. The electric flux linked to the surface in uint of V−m is

View SolutionIn a uniform electric field find the total flux associated with the given surfaces

View SolutionA square frame of edge 10 cm is placed with its positive normal making on angle of 600 with a uniform electric field of 20Vm−1. Find the flux of the electric field through the surface bounded by the frame.
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is

View Solutiona hemispherical hollow body is placed in a uniform electric field E. the total flux linked with the curved surface is

View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionPQRS is a square region of side 2a in the plane of paper. A uniform magnetic field B, directed perpendicular to the plane of paper and into its plane is confined within this square region. A square loop of side 'a' and made of a conducting wire of resistance R is moved at a constant velocity →v from left to right in the plane of paper as shown. Obviously, the square loop will enter the magnetic field at some time and then leave it after some time. During the motion of loop, whenever magnetic flux through it changes, emf will be induced resulting in induced current. Let the motion of the square loop be along x-axis and let us measure x coordinate of the centre of square loop from the centre of the square magnetic field region (taken as origin). Thus, x coordinate will be positive if the centre of square loop is to the right of the origin O (centre of magnetic field) and negative if centre is to the left.

For x=a/4
(i) magnetic flux through the loop,
(ii) induced current in the loop and
(iii) external force required to maintain constant velocity of the loop, will be
View Solution