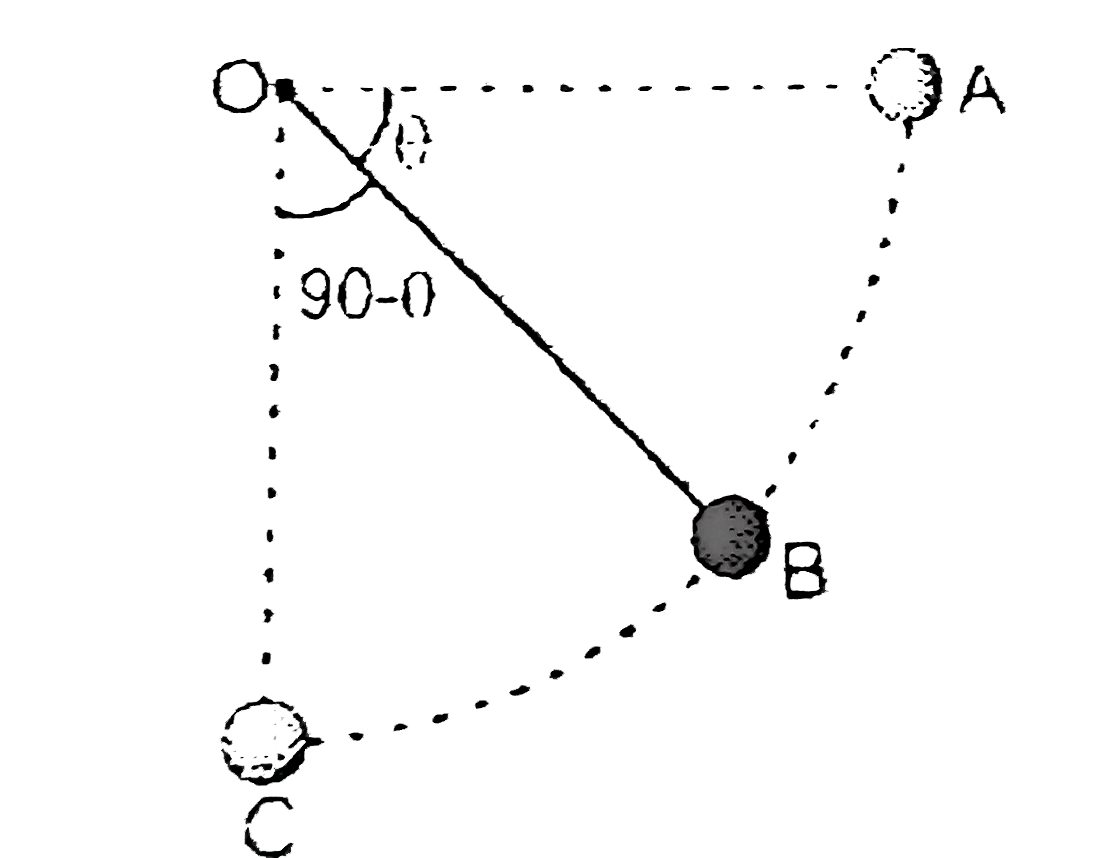
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. the ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2 let the velocity of ball at B is →vB and at C is →vC respectively.
Q. If |→vC|=2|→vB| then the value of θas shown is
cos−1(1)4
sin−1(1)4
cos−1(1)2
sin−1(1)2
The correct Answer is:B
VB=√2gLsinθ and VC=√2gL
VC=2VB
Then 2gL=4(2gLsinθ)
or sinθ=14 or θ=sin−1(14)
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
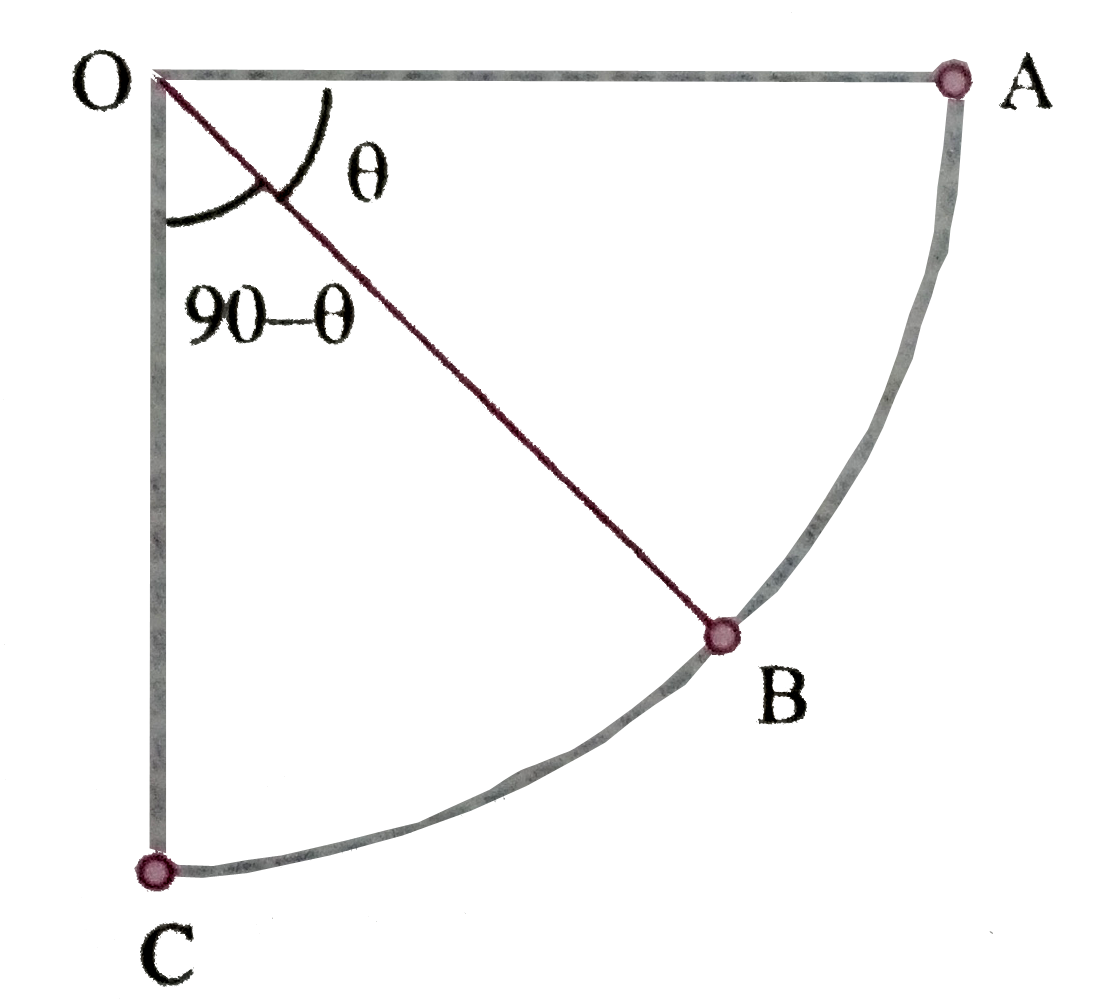
If |→vC=2|→vB∣ then the value of θ as shown is
View SolutionA bob of mass m is connected by string of length L to point P. The system is released from rest with the pendulum bob in a horizontal position. Which of the following graph is correctly showing the variation of T (tension) with Ɵ?
View Solution
Knowledge Check
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
Two block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionA simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionBall A is thrown up vertically with speed 10ms. At the same instant another ball B is released from rest at height h. At time t, the speed of A relative to B is
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA ball is held at rest in position A by two light cords. The horizontal cord is now cut and the ball swings to the position B. What is the ratio of the tension in the cord in position B to that in position A?
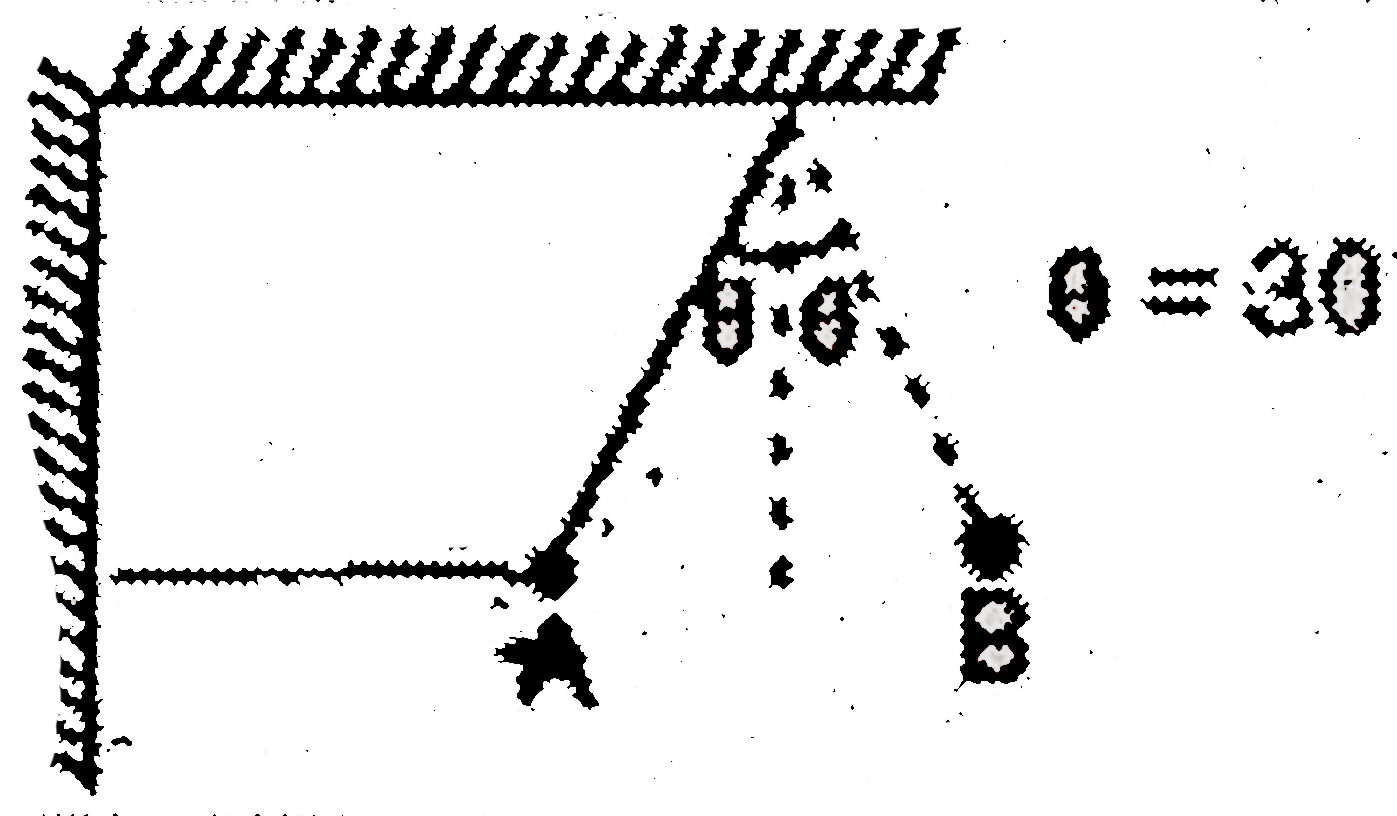
View SolutionOne end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View SolutionA ball is released from point A. During its motion ball takes two seconds from B to C Find the time taken by ball from A to C.
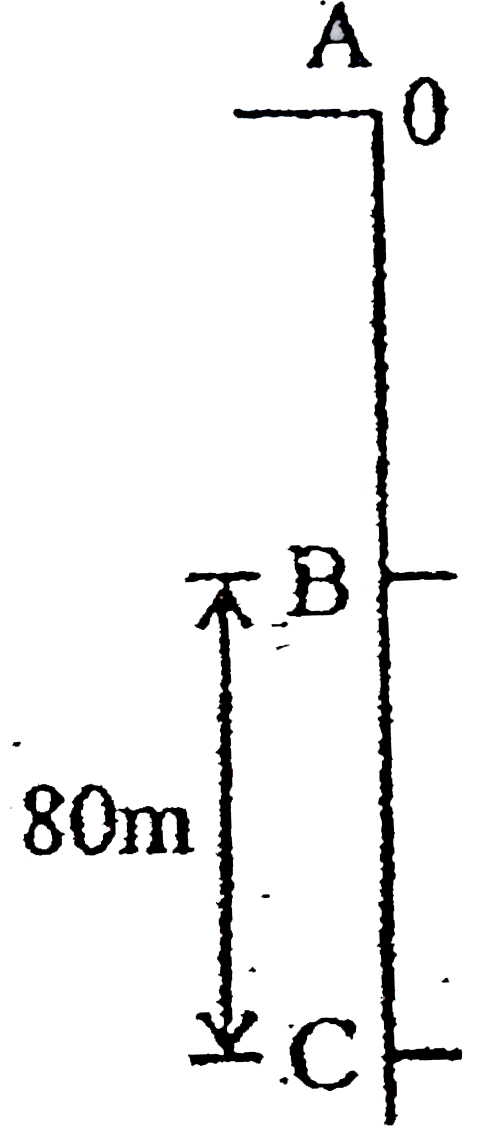 .
.
View Solution
