Four identical rods of mass M=6kg each are welded at their ends to form a square and then welded to a massive ring having mass m=4kg and radius R=1m. If the system is allowed to roll down the incline of inclination θ=30∘, determine the minimum value of the coefficient of static friction that will prevent slipping.
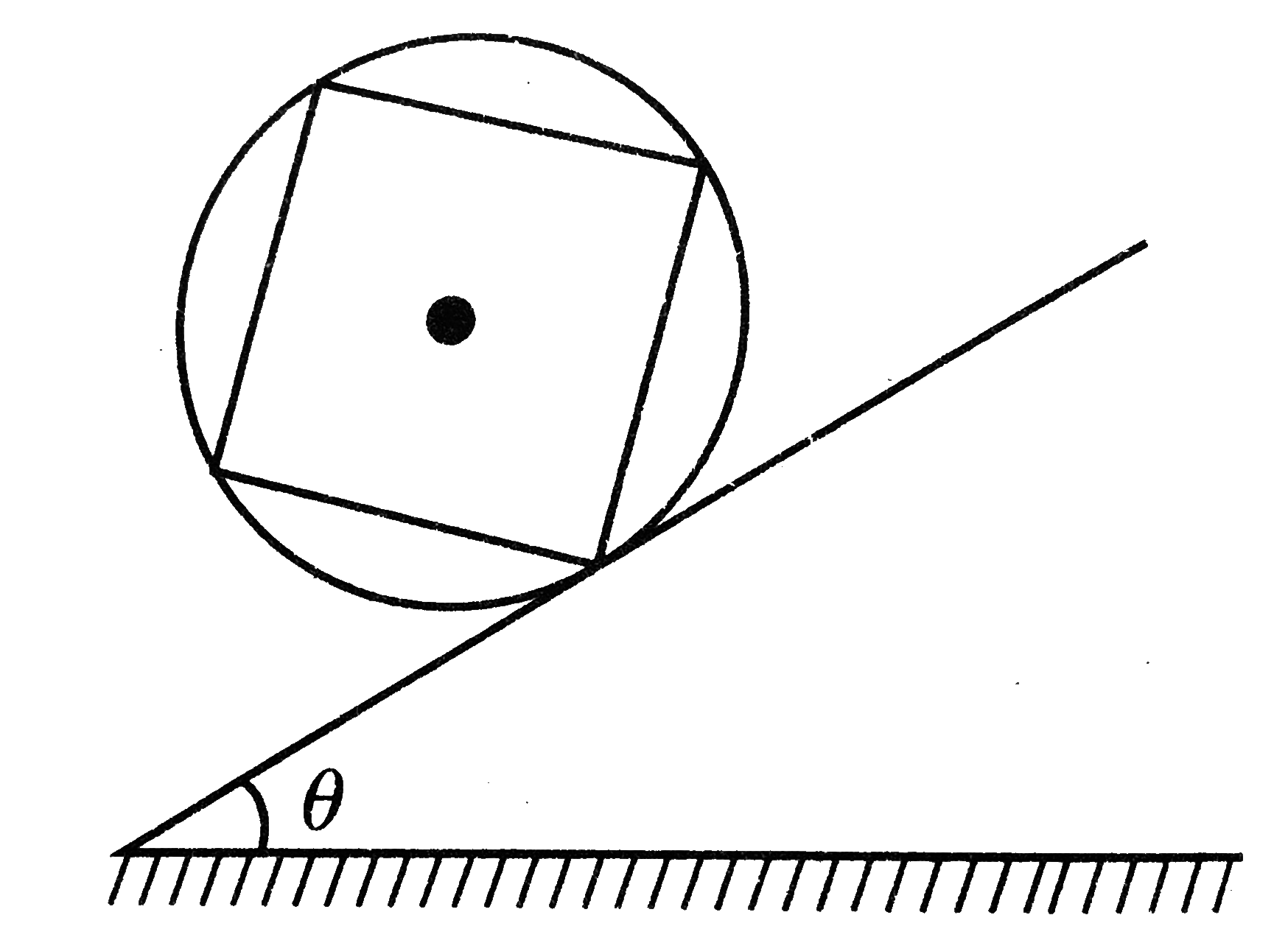
The moment of inertia of the system about the centre of ring will be
57
512√3
5√37
75√3
The correct Answer is:B
i=⎡⎢
⎢
⎢⎣M(R√2)212+M(R√2)2⎤⎥
⎥
⎥⎦×4+mR2
=20kgm2.
(4M+m)gsinθ−F=(4M+m)a.
F.R.=I(aR)
Solving
a=7g24
F=20a≤μ(4M+m)gcos30
μ≥512√3
∴μmin=512√3
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 707videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 718videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 695videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
Four identical uniform rods of mass m=6kg each are welded their ends to form a square and then welded to a uniform ring having mass m = 4 kg and radius R = 1 m. The system is allowed to roll down a rough incline of inclination θ=30∘. (where g in ms−2)
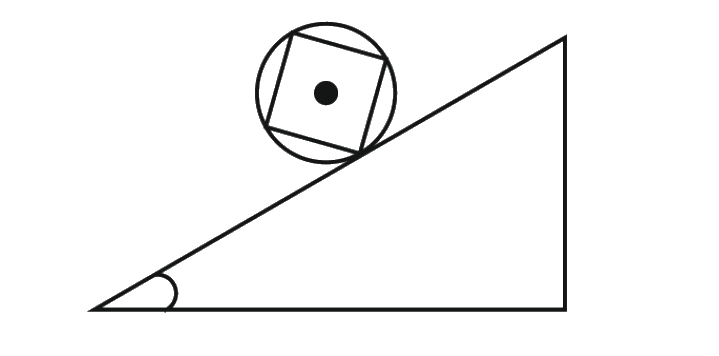
The force of friction between the system and the plane isView Solution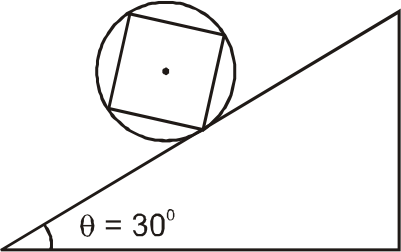
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The acceleration of centre of mass of system isView Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder rolls without slipping down a 30∘ slope. The minimum coefficient of friction needed to prevent slipping, will be
A0.192B0.18C0.15D0.2
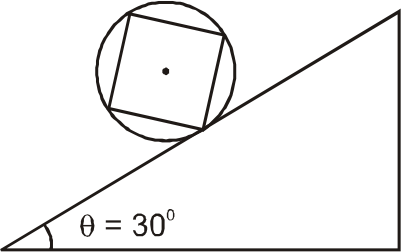
Four identical uniform rods of mass M=6kg each are welded at their ends to form a square and then welded to a uniform ring having mass m=4kg & radius R=1m the system is allowed to roll down on the rough and fixed incline of inclination θ=30∘ (assume no sliding anywhere)
Q. The moment of inertia of system about the axis of ring will be-View SolutionFor identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k10 . Find the value of k.
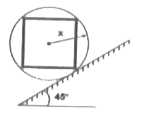View SolutionA spherical shell of radius R is rolling down an incline of inclination θ without slipping. Find minimum value of coefficient of friction.
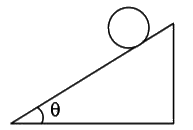View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
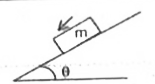View SolutionA sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
View SolutionA solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
View SolutionA solid sphere of mass m rolls without slipping on an inlined plane of inclination 0. what shoul be the minimum coefficient of static feiction to support pure rolling?
View Solution