One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
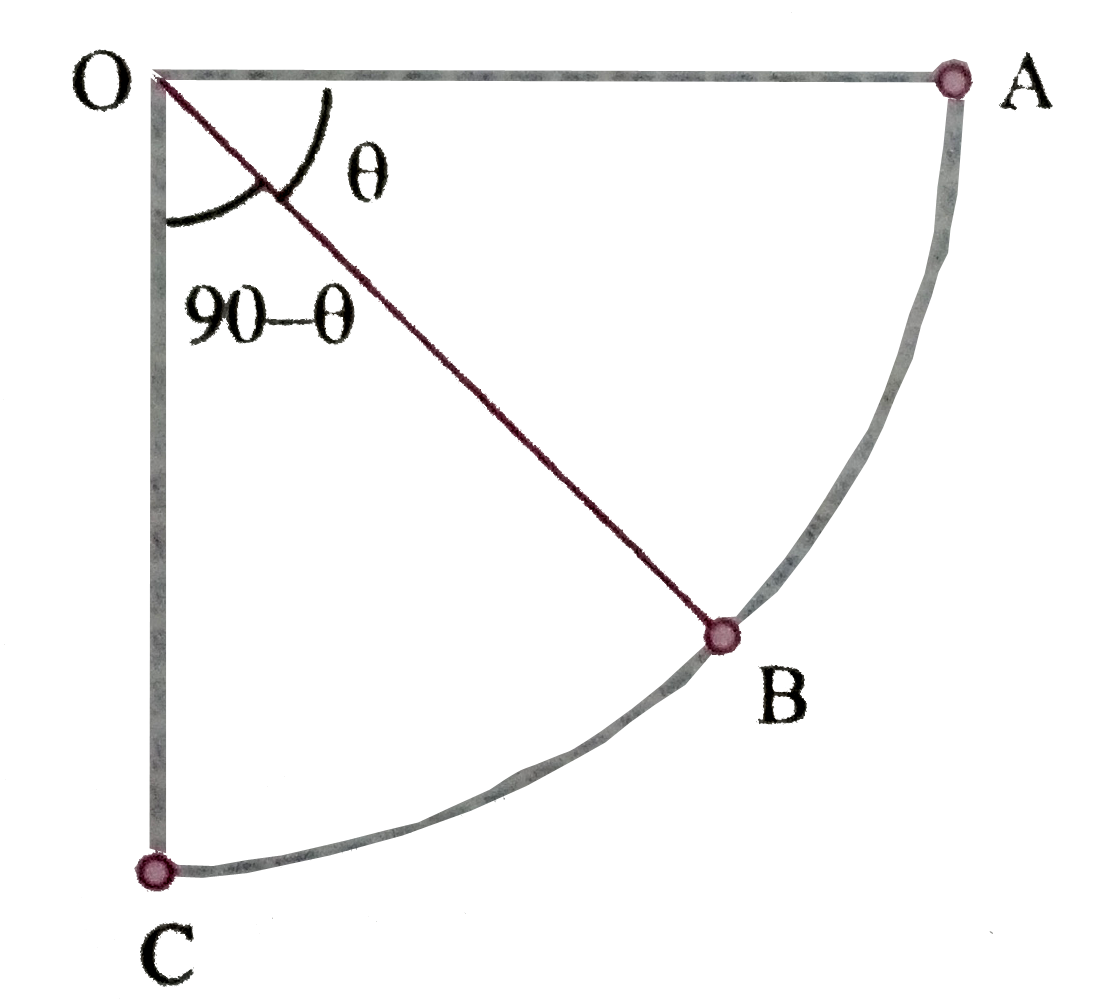
If |→vC=2|→vB∣ then the value of θ as shown is
cos−1(14)
sin−1(14)
cos−1(12)
sin−1(12)
The correct Answer is:B
vB=√2gLsinθ and vC=√2gL
if VC=2vB
Then 2gL=4(2gLsinθ)
or sinθ14orθsin−1(14)
Similar Questions
A bob of mass m is connected by string of length L to point P. The system is released from rest with the pendulum bob in a horizontal position. Which of the following graph is correctly showing the variation of T (tension) with Ɵ?
View SolutionBall A is thrown up vertically with speed 10ms. At the same instant another ball B is released from rest at height h. At time t, the speed of A relative to B is
View Solution
Knowledge Check
A ball A is thrown up vertically with a speed u and at the same instant another ball B is released from a height h. At time t, the speed A relative to B is
AuBu - 2gtC√u2−2ghDu - gt
A simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionA price of length 1 m and mass 1 kg is suspended vertically from one end of a massless string passing on asmooth , fixed pulley . A ball of mass 2 kg is attached to the other end from the position shown . Time taken by the ball to cross the pipe is shown. Time taken by the ball to cross the pipe is
View SolutionOne end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
At the highest position of ball, tangential acceleration of ball is −
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA ball is released from point A. During its motion ball takes two seconds from B to C Find the time taken by ball from A to C.
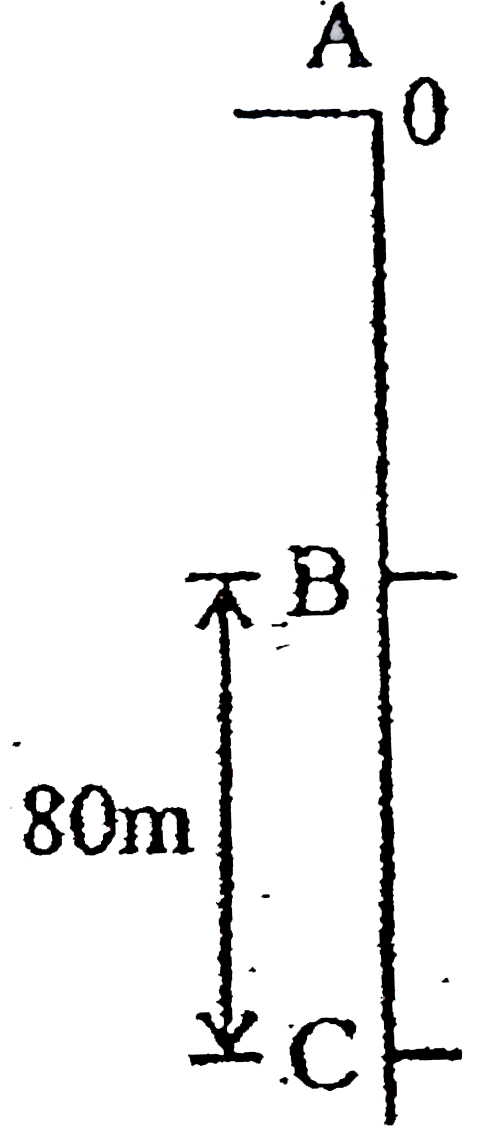 .
.
View Solution
