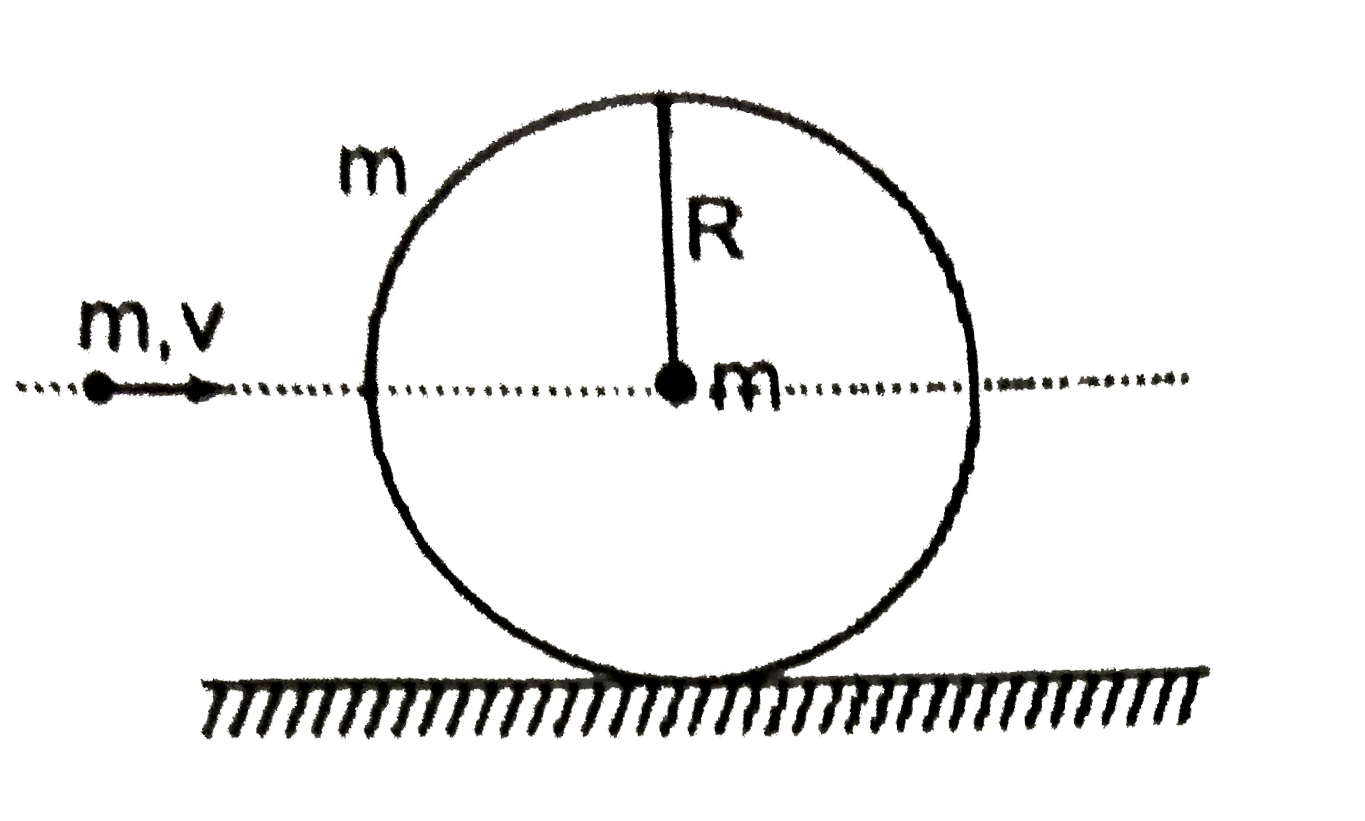
A hollow sphere of mass 'm' and radius R rests on a smooth horizontal surface. A simple pendulum having string of length R and bob of mass m hangs from top most point of the sphere as shown. A bullet of mass 'm' and velocity 'v' partially penetrates the left side of the sphere and stick to it. The velocity of the sphere just after collision with bullet is .
v2
v3
2v3
3v5
The correct Answer is:A
For the duration of collision the pendulum does not exert any force on the sphere in the horizontal direction.
Hence the horizontal momentum of bullet + sphere is conserved for the duration of collision . Let v' be the velocity of bullet and sphere just after the collision.
∴ from conservation of momentum ltbr> (m+m)v'=mv
or v'=v2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 57
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 55
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A solid sphere of mass M and radius R is pulled horizontally on a rough surface as shown in Fig. Choose the incorrect alternatives.

View SolutionA hollow sphere of mass 'm' and radius 'R' are placed on horizontal surface and a horizontal force 'F' starts acting at a distance 'x' from its top most as shown in the figure.The value of 'x' such that hollow sphere starts pure rolling without use of friction is
_PHY_E05_157_Q01.png)
View Solution
Knowledge Check
A sphere of mass m moving with a constant velocity u hits another stationary sphere of the same mass. If e is the coefficient of restitution, then ratio of velocities of the two spheres after collision will be
A1−e1+eB1+e1−eCe+1e−1De−1e+1A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A wooden log of mass M and length L is hinged by a frictionless nail at O.A bullet of mass m strikes with velocity v and sticks to it. Find angular velocity of the system immediately after the collision aboutO.

View SolutionA thin hollow sphere of mass m=2kg, radius=(1/2)m is sliding on a horizontal surface with a constant frequency n = 60 rpm. Find the total mechanical energy of the hollow sphere.
View SolutionSphere A of mass m moving with a constant velocity u hits another stationary sphere B of the same mass. If e is the co-efficient of restitution, then ratio of velocities of the two spheres vA:vB after collision will be :
View Solution
A hollow sphere of mass m and radius R is placed on smooth gound. A particle of mass m is projected with velocity v0 and angle θ lowest point a inside the sphere as shown in diagram if particle strikes the sphere at a point which is on horizontal level of centre and at that moment particle is at highest point. The collision between particle and sphere is elastic. The value of v0 is
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View Solution
