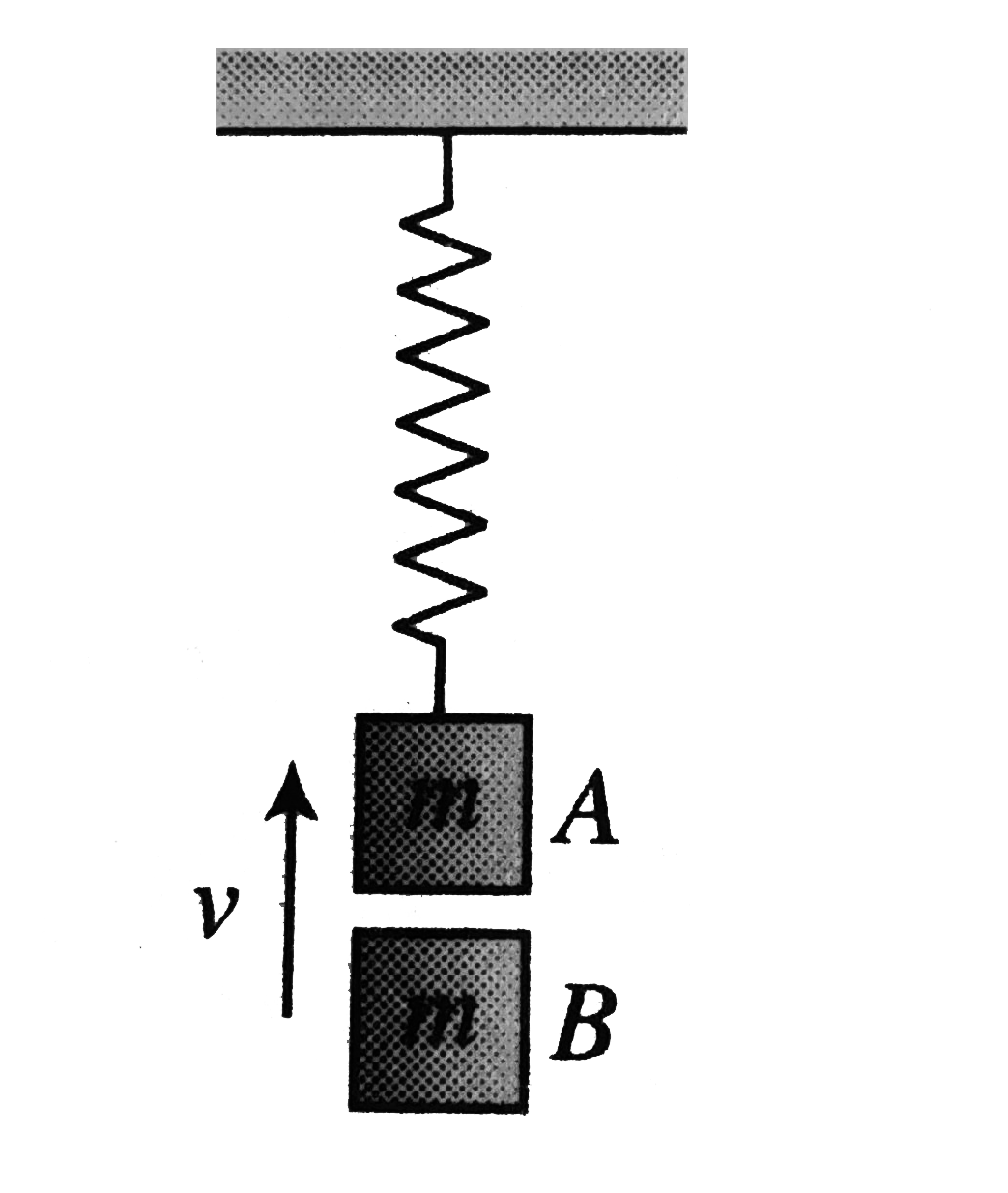
Block A is hanging from a vertical spring and is at rest. Block B strikes block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
√60mg2k
√60mg2k
√10mg2k
None of these
The correct Answer is:B
(B) The initial extension in spring is x0=mgk Just after collision of B with A the speed of combined mass is v2.
For the spring to just attain natural length the combined mass must rise up by x0=mgk( sec. fig. ) and comes to rest.

Applying conservation of energy between initial and final states
122m(v2)2+12k((mg)?(k))2=2mg(mgk)
Solving we get v=√6mg2k
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 57
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 55
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Block A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is

View SolutionBlock A is hanging from a vertical spring and is at rest. Block B strikes the block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is

View SolutionBlock A is hanging from vertical spring of spring constant K and is rest. Block B strikes block A with velocity v and sticks to it. Then the value of v for which the spring just attains natural length is
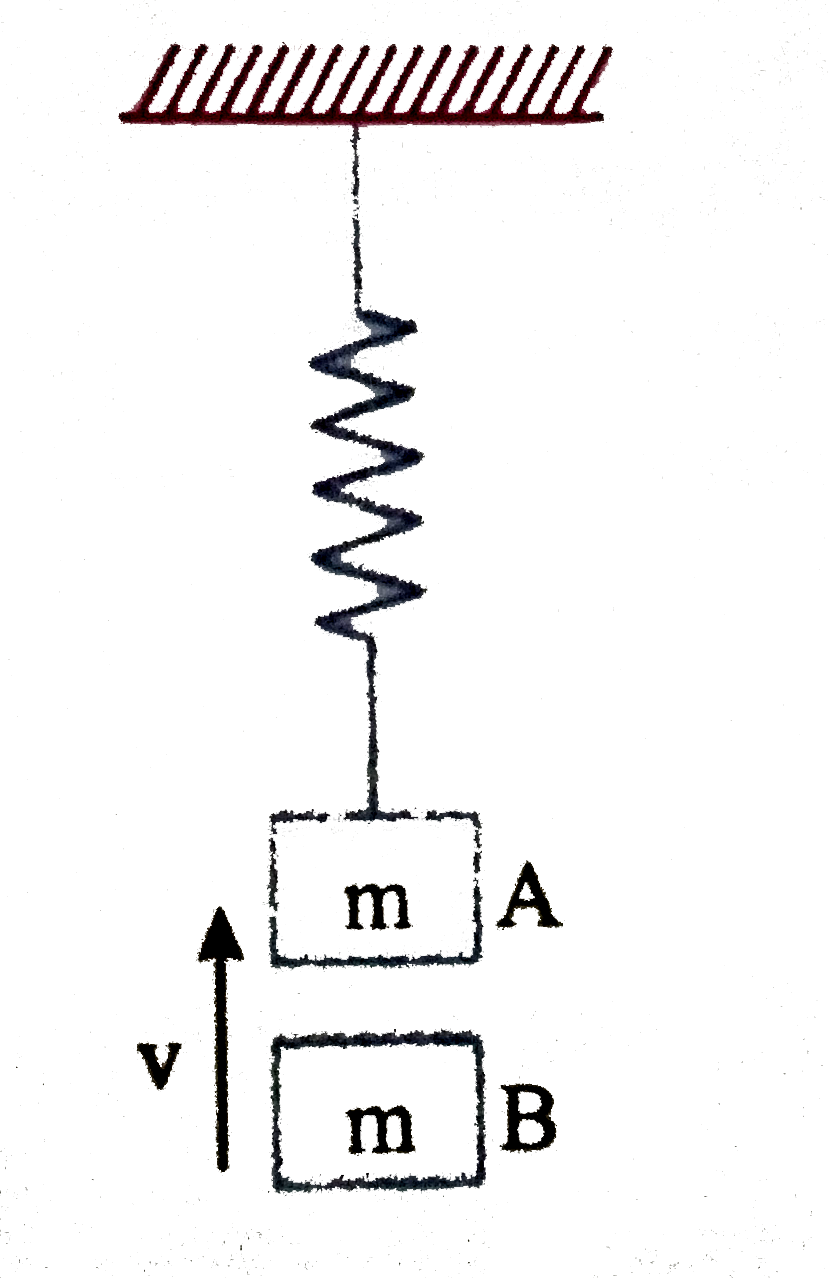
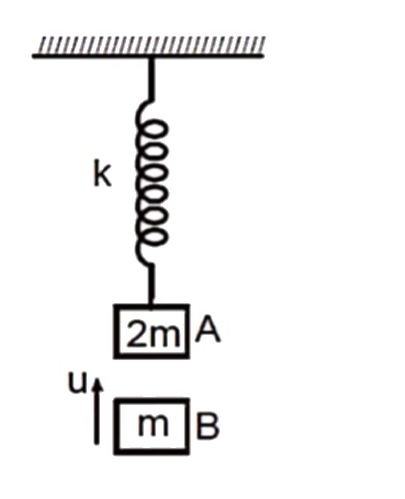
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
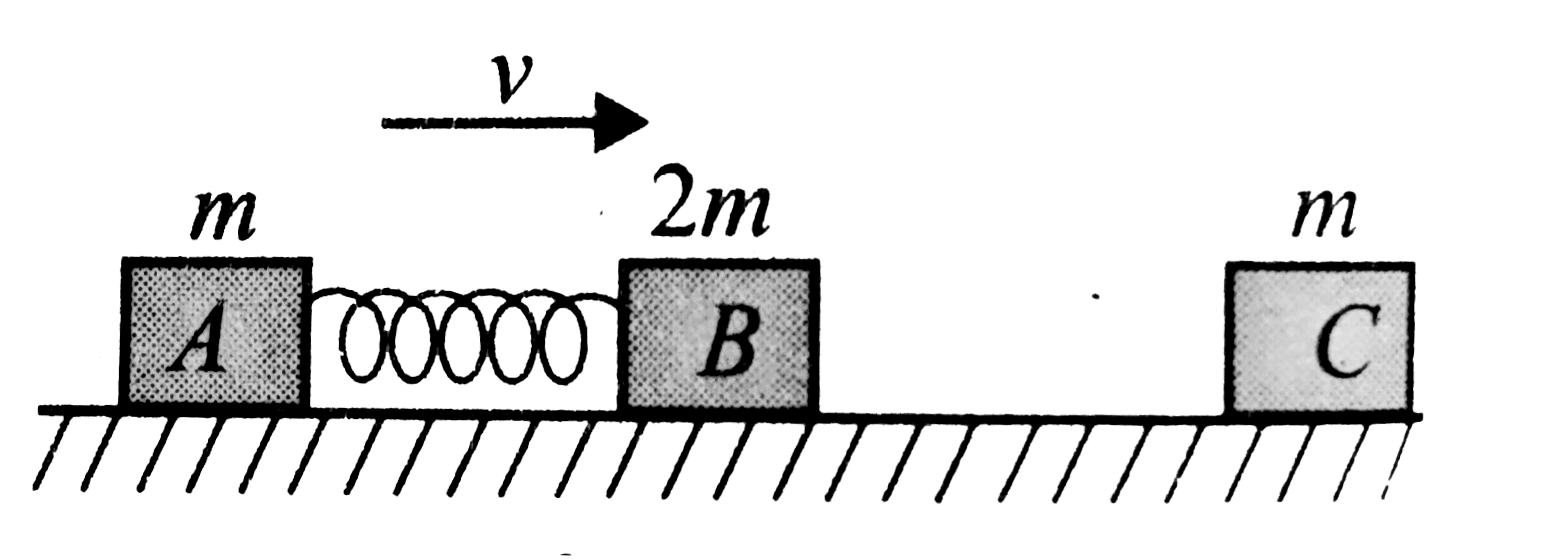
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionAssertion: Two blocks A and B are connected at the two ends of an ideal spring as shwon in figure. Initially, spring was released. Now block B is pressed. Linear momentum of the system will not remain constan till the spring reaches its initial natural length.
Reason: An external force will act from the wall on block A.
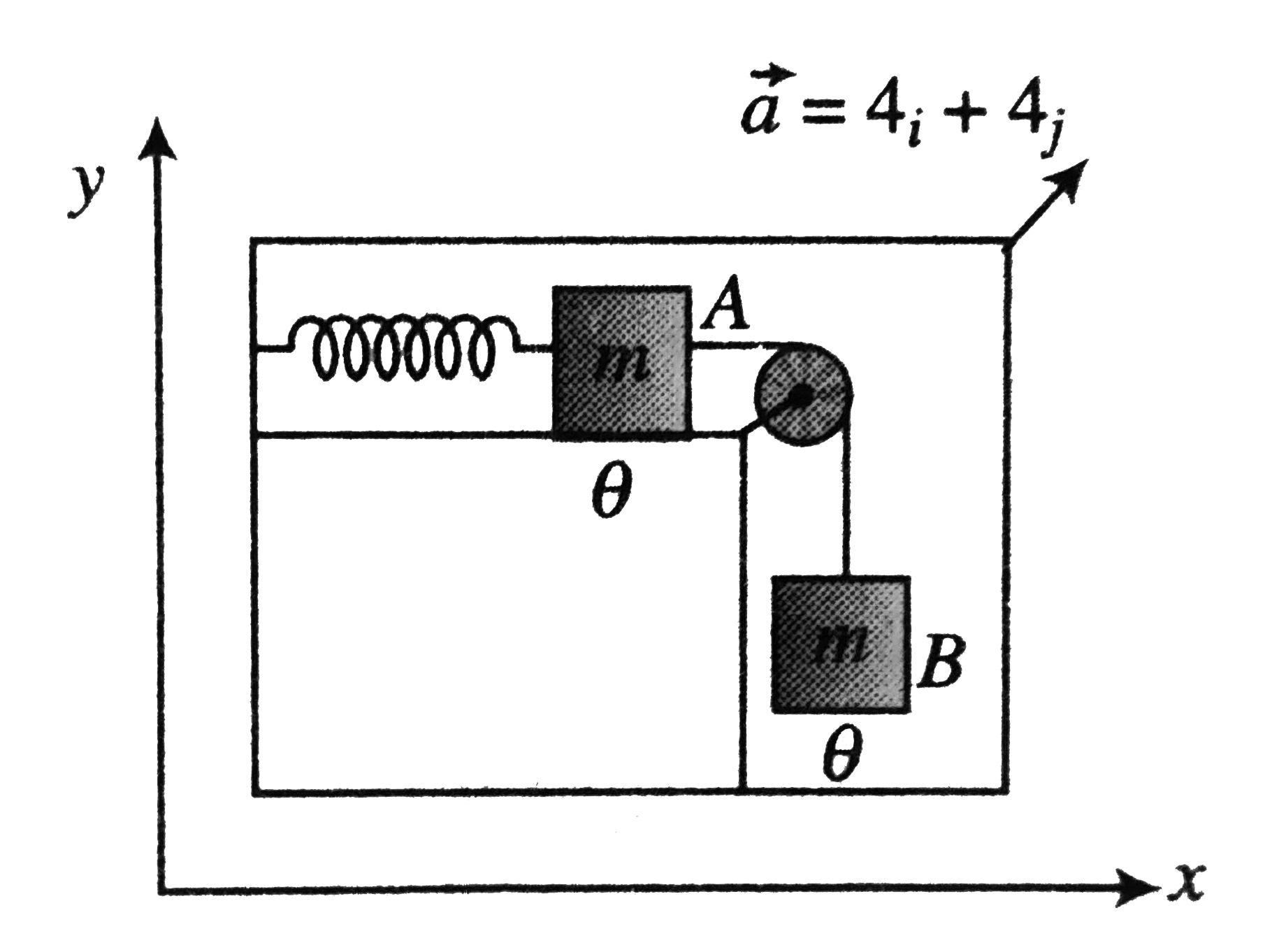
View SolutionThe arrangement shown in figure is at rest. An ideal spring of natural length l0 having spring constant k=220Nm−1, is connected to block A. Blocks A and B are connected by an ideal string passing through a friction less pulley. The mass of each block A and B is equal to m=2kg when the spring was in natural length, the whole system is given an acceleration →a as shown. If coefficient of friction of both surfaces is μ=0.25, then find the maximum extension in 10(m) of the spring. (g=10ms−2).
View Solution
