The moment of inertia of a door of mass m, length 2l and width l about its longer side is
11ml224
5ml224
ml23
none of these
The correct Answer is:C
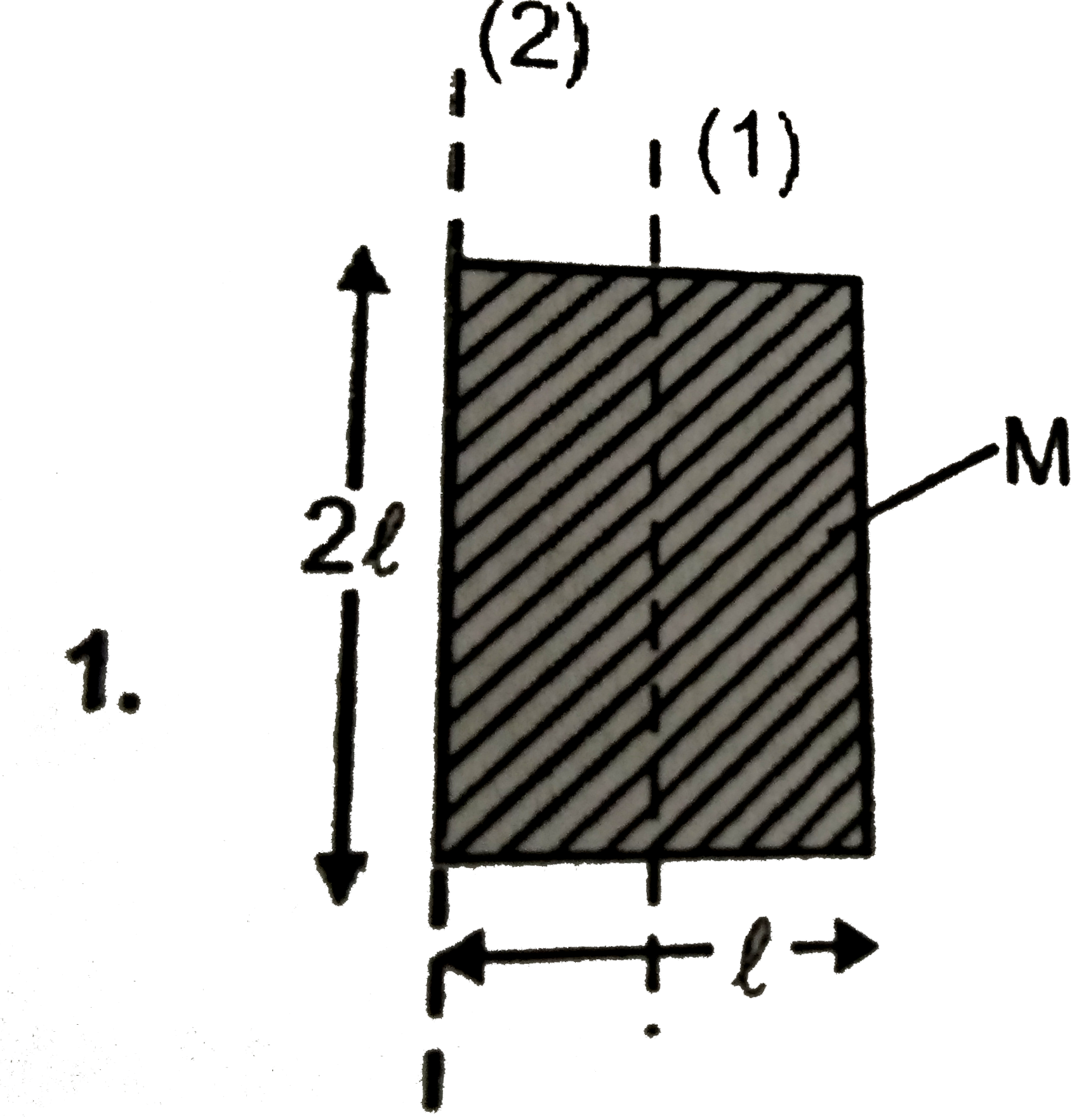 I2=ml23.
I2=ml23.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 56
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
The moment of inertia of a door of mass m, length 2l and width l about its longer side is.
View SolutionThe moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
View SolutionIn Fig. find moment of inertia of a plate having mass M, length l and width b about axes 1,2,3 and 4. Assume that C is the centre and mass is uniformly distributed.
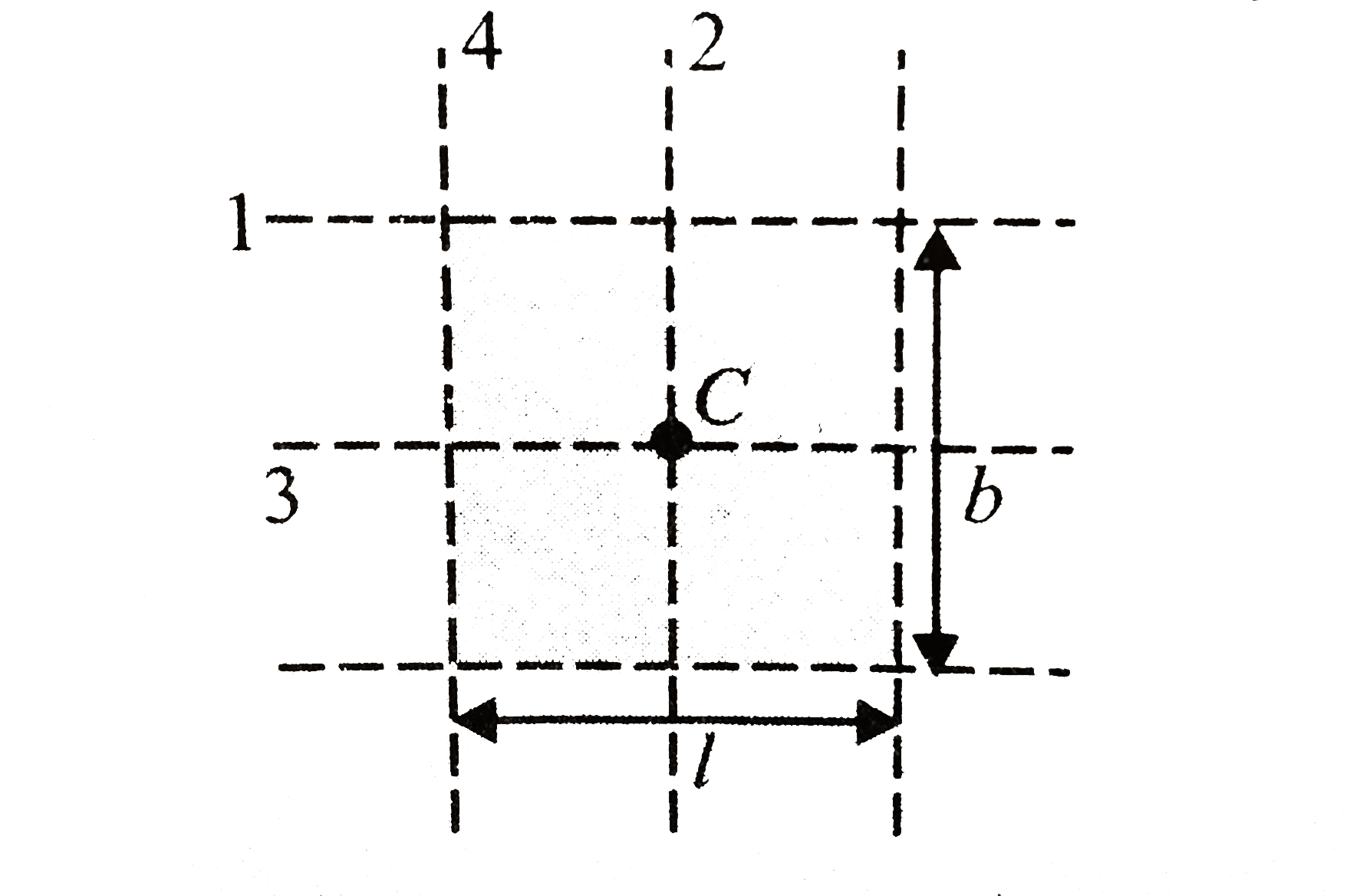
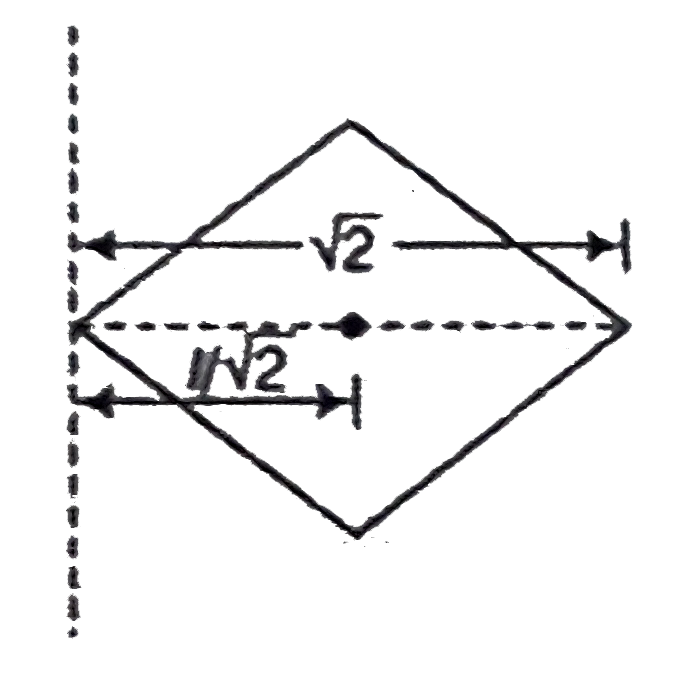
View SolutionThe moment of inertia of a system of four rods each of length l and mass m about the axis shown is
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionMoment of inertia of a rod of mass m and length l about its one end is I. If one-fourth of its length is cut away, then moment of inertia of the remaining rod about its one end will be
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View Solution
