In the figure, the block B of mass m starts from rest at the top of a wedge W of mass M. All surfaces are without friction. W can slide on the ground. B slides down onto the ground, moves along it with a speed v, has an elastic collision with the wall, and climbs back on to W.

B will reach the top of W again
from the beginning, till the collision of with the wall, the centre of mass 'B+W' is stationary in horizontal direction
after the collision the centre of mass 'B+W' moves with the velocity 2mvm+M
when B reaches its highest position on W, the speed of W is 2mvm+M
The correct Answer is:B, C, D
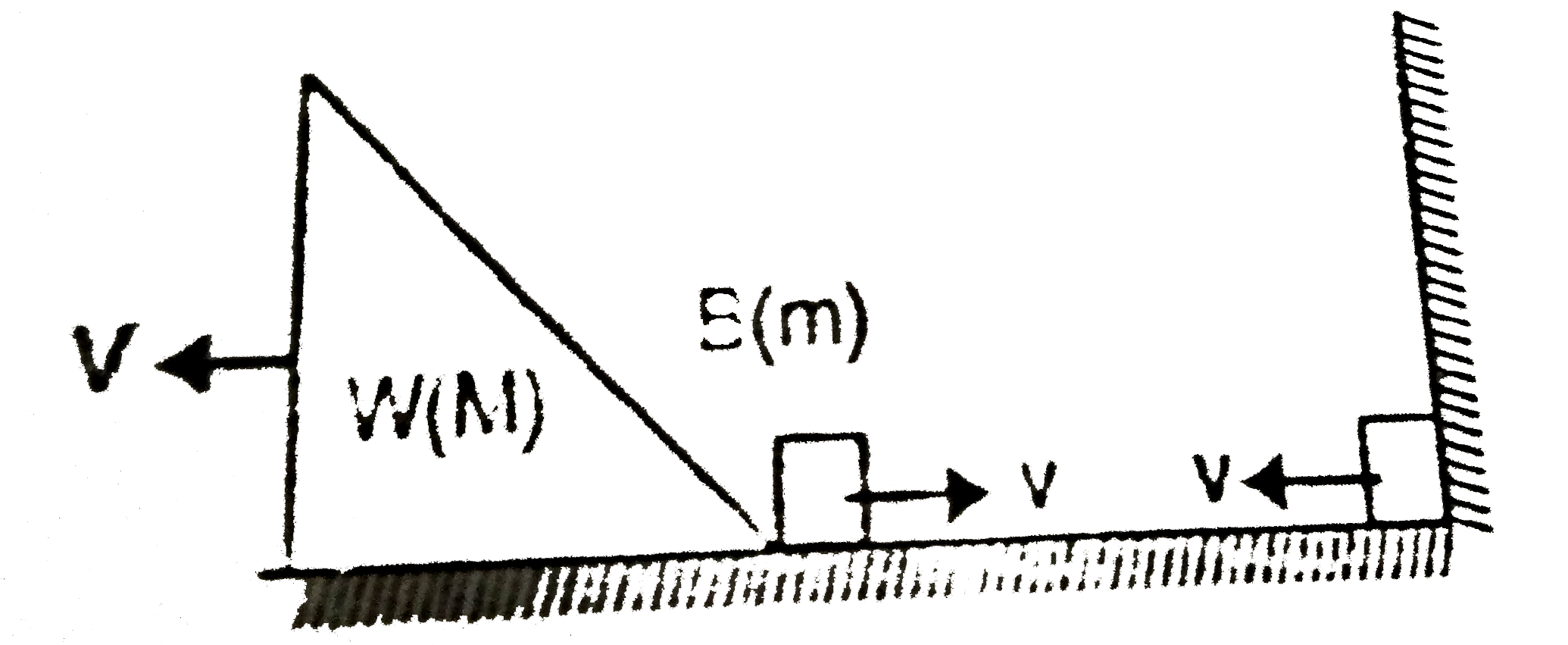
From linear conservation
mv=MV
V=mVM
After the elastic collision with wall speed of the block B remain same in the direction V
Vcm=m(v)+M(mvM)m+M
=2mVm+M
When block B will reach at maximum height on wedge
From momentum conservation
mvMM+mv=(m+M)Vc
VC=2mv(M+m).
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 58
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 59
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 56
7 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A block of mass 'M' is placed on the top of a wedge of mass '4M'. All the surfaces are frictionless. The system is released from rest. The distance moved by the wedge at the instant, the block reaches the bottom will be

View SolutionA block of mass m is stationary with respect to the wedge of mass M moving with uniform speed v on horizontal surface. Work done by friction force on the block in t seconds is
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
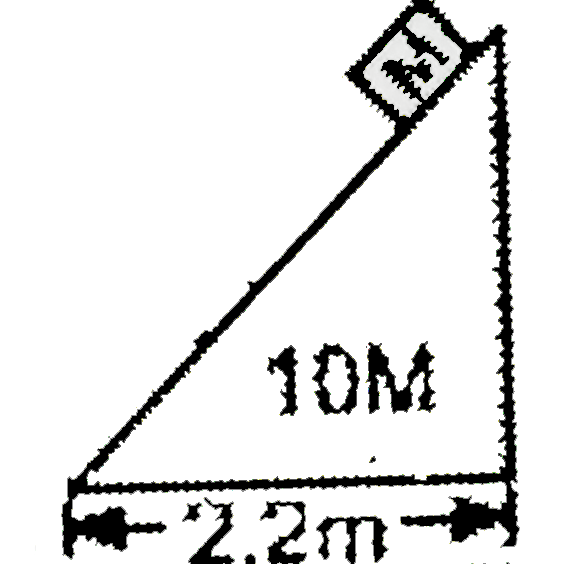
View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
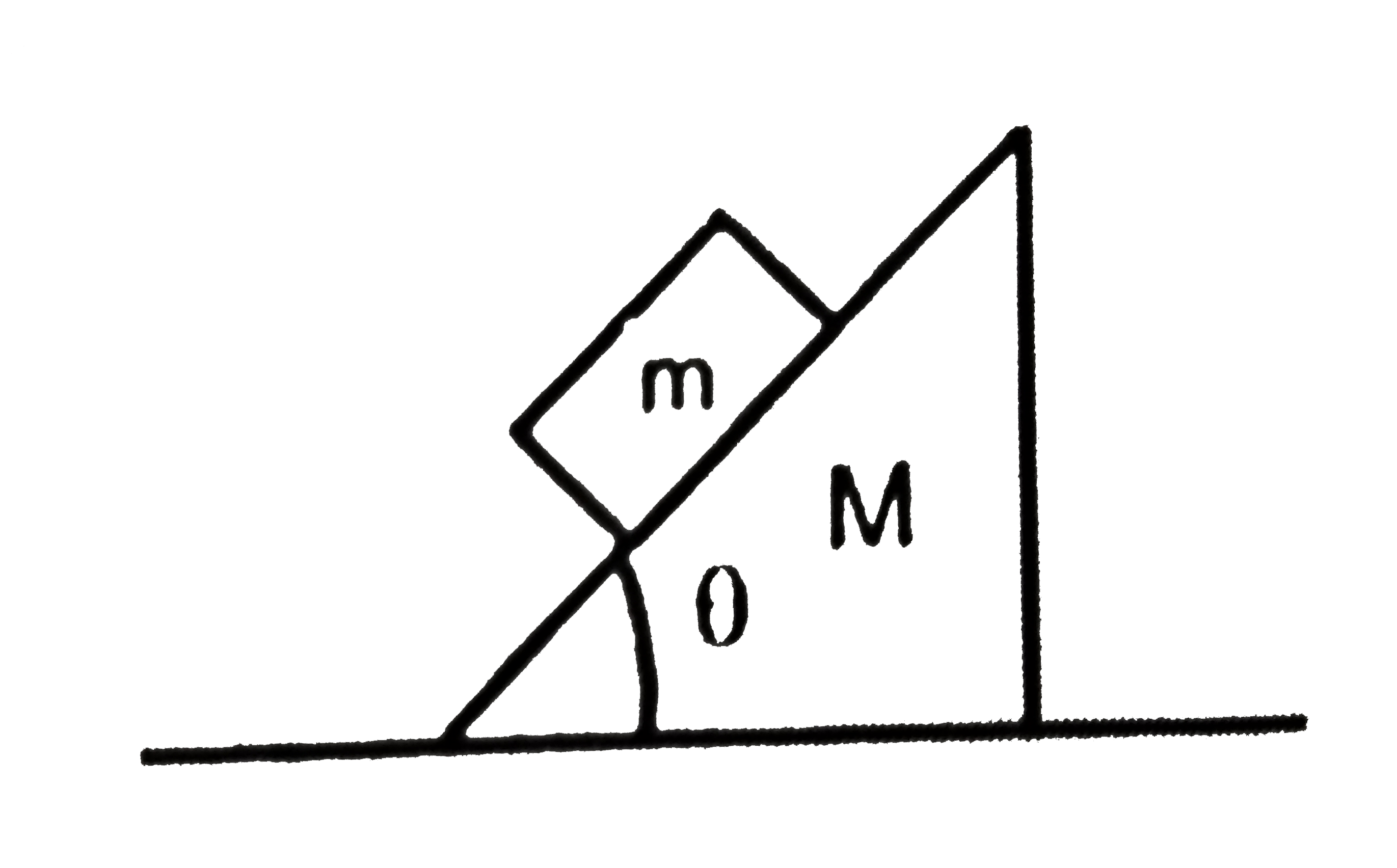
View SolutionA block of mass m lies on wedge of mass Mas shown in figure. Find the minimum friction coeffcient required between wedge Mand ground so that it does not move while block m slips down on it.
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionBlock B has mass m and is released from rest when it is on top of wedge A, which has a mass 3m. Determine the tension in cord CD needed to hold the wedge from moving while B is sliding down A. Neglect friction.

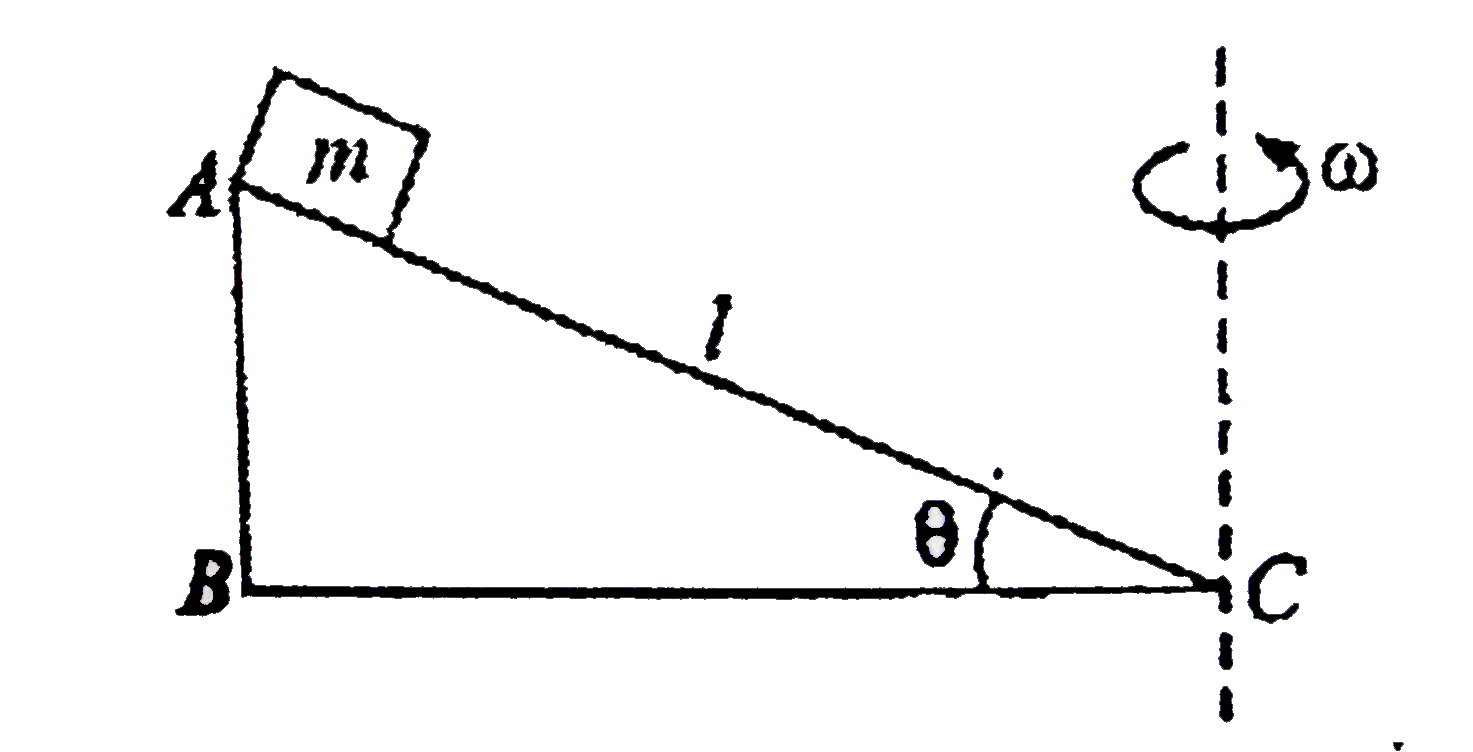
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
View SolutionA block of mass m is placed on the top of bigger wedge M. All the surfaces are frictionless. The system is released from rest. Find the distance moved by smaller block (w.r.t. triangular wedge) when bigger wedge travel distance X on plane surface
_PHY_E05_232_Q01.png)
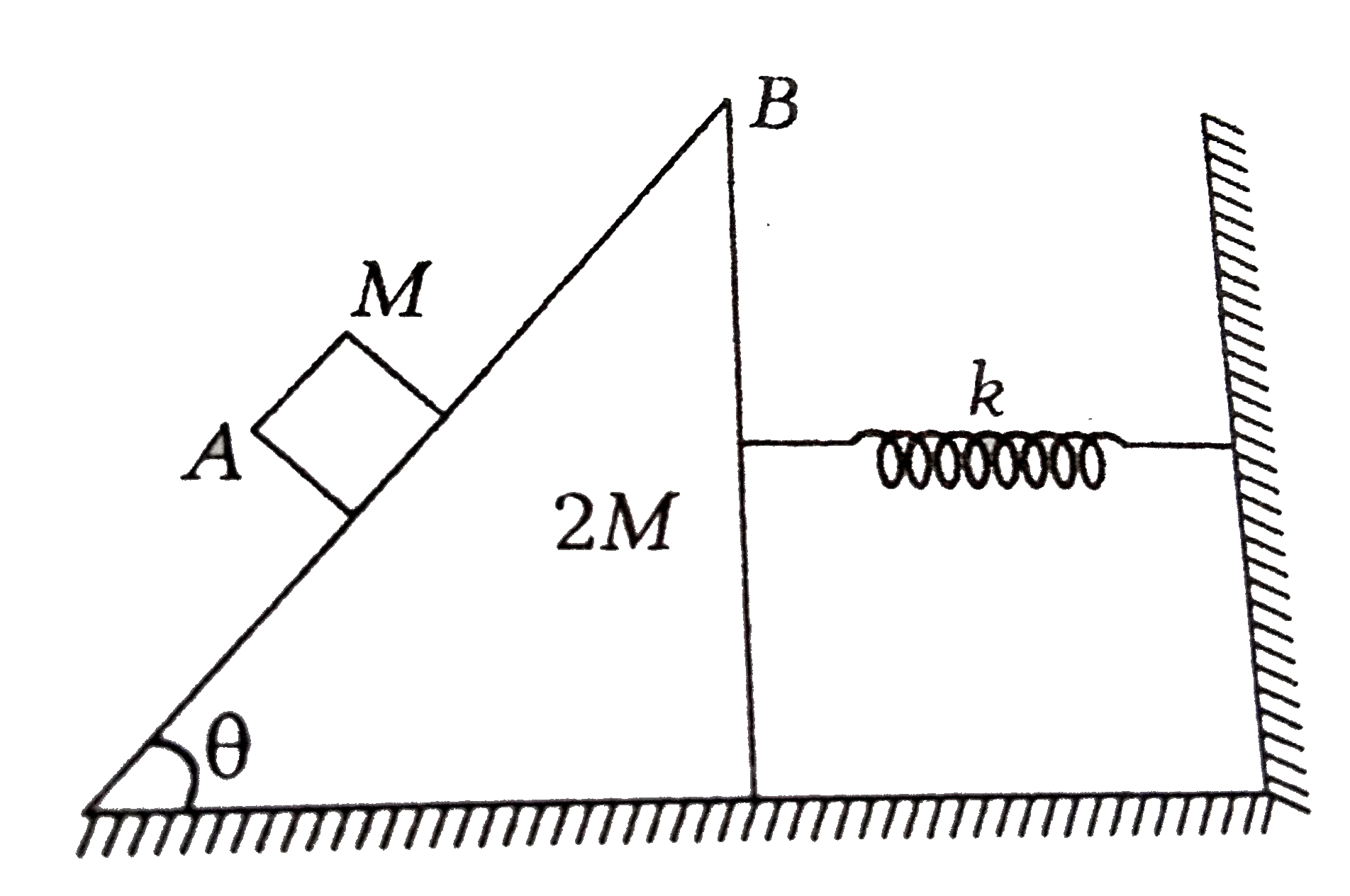
View SolutionA block A of mass M rests on a wedge B of mass 2M and inclination θ. There is sufficient friction between A and B so that A does not slip on B. If there is no friction between B and ground, the compression in spring is
View Solution
