A thin hollow sphere of mass m=2kg, radius=(1/2)m is sliding on a horizontal surface with a constant frequency n = 60 rpm. Find the total mechanical energy of the hollow sphere.
To find the total mechanical energy of a thin hollow sphere sliding on a horizontal surface, we will consider both its translational and rotational kinetic energy. Here’s the step-by-step solution:
Step 1: Convert the frequency to angular velocity
The frequency n is given as 60 revolutions per minute (rpm). We need to convert this to radians per second.
ω=n×2π radians1 revolution×1 minute60 seconds
Substituting the value of n:
ω=60×2π60=2π radians/second
Step 2: Identify the mass and radius of the sphere
The mass m of the sphere is given as 2 kg, and the radius r is given as 12 m.
Step 3: Calculate translational kinetic energy
The translational kinetic energy KEtrans is given by:
KEtrans=12mv2
Since the sphere is rolling without slipping, the linear velocity v can be expressed as:
v=rω
Substituting for v:
v=12×2π=π m/s
Now substituting v into the translational kinetic energy formula:
KEtrans=12×2×(π)2=π2 Joules
Step 4: Calculate rotational kinetic energy
The moment of inertia I of a thin hollow sphere about its center is given by:
I=23mr2
Substituting the values:
I=23×2×(12)2=23×2×14=13 kg m2
The rotational kinetic energy KErot is given by:
KErot=12Iω2
Substituting I and ω:
KErot=12×13×(2π)2=16×4π2=2π23 Joules
Step 5: Calculate total mechanical energy
The total mechanical energy E is the sum of translational and rotational kinetic energy:
E=KEtrans+KErot
Substituting the values:
E=π2+2π23
Finding a common denominator:
E=3π23+2π23=5π23 Joules
Step 6: Numerical approximation
Calculating the numerical value:
E≈5×(3.14)23≈5×9.863≈49.33≈16.43 Joules
Thus, the total mechanical energy of the hollow sphere is approximately 16.43 Joules.
---
The frequency n is given as 60 revolutions per minute (rpm). We need to convert this to radians per second.
The mass m of the sphere is given as 2 kg, and the radius r is given as 12 m.
The translational kinetic energy KEtrans is given by:
The moment of inertia I of a thin hollow sphere about its center is given by:
The total mechanical energy E is the sum of translational and rotational kinetic energy:
Calculating the numerical value:
Similar Questions
A disc of mass 4.8 kg and radius 1 m is rolling on a horizontal surface without sliding with angular velocity of 600 rotations/min. What is the total kinetic energy of the disc ?
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA solid sphere of radius r is rolling on a horizontal surface. The ratio between the rotational kinetic energy and total energy.
View SolutionCalculate the kinetic energy of a hollow metal sphere of mass 2 kg, which rolls over a horizontal surface with a linear velocity of 20 cm/s ?
View SolutionA sphere of mass m and radius R rolls without sliding on a horizontal surface. It collides with a light spring of stiffness K with a kinetic energy E. If the surface (AB) under the spring is smooth, find the maximum compression of the spring.
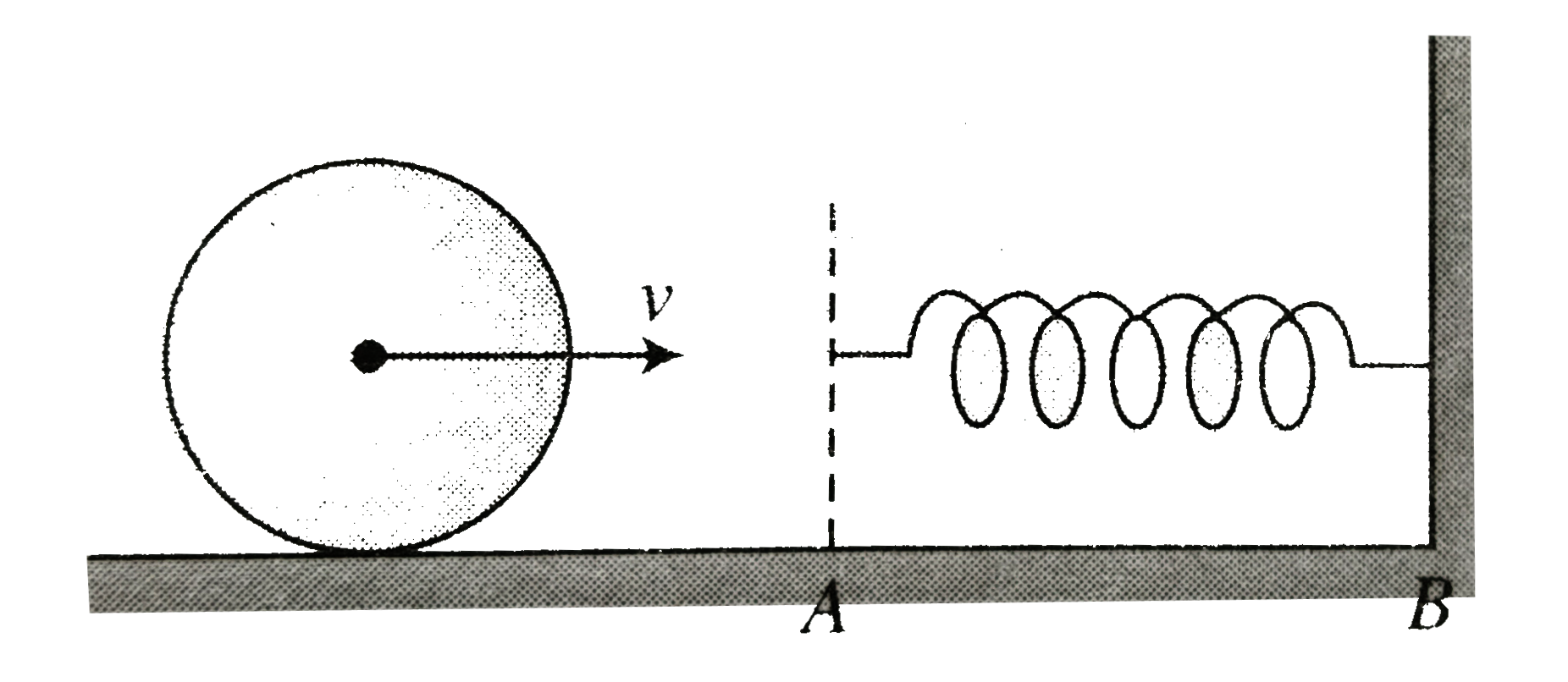
View SolutionA horizontal force of 1N is needed to keep a block of mass 0.25kg sliding on a horizontal surface with a constant speed. Find the coefficient of sliding friction. (g=10ms−2)
View SolutionA point mass m is released from rest at a distance of 3R from the centre of a thin-walled hollow sphere of radius R and mass M as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point P at a distance R/2 from the centre of the sphere is
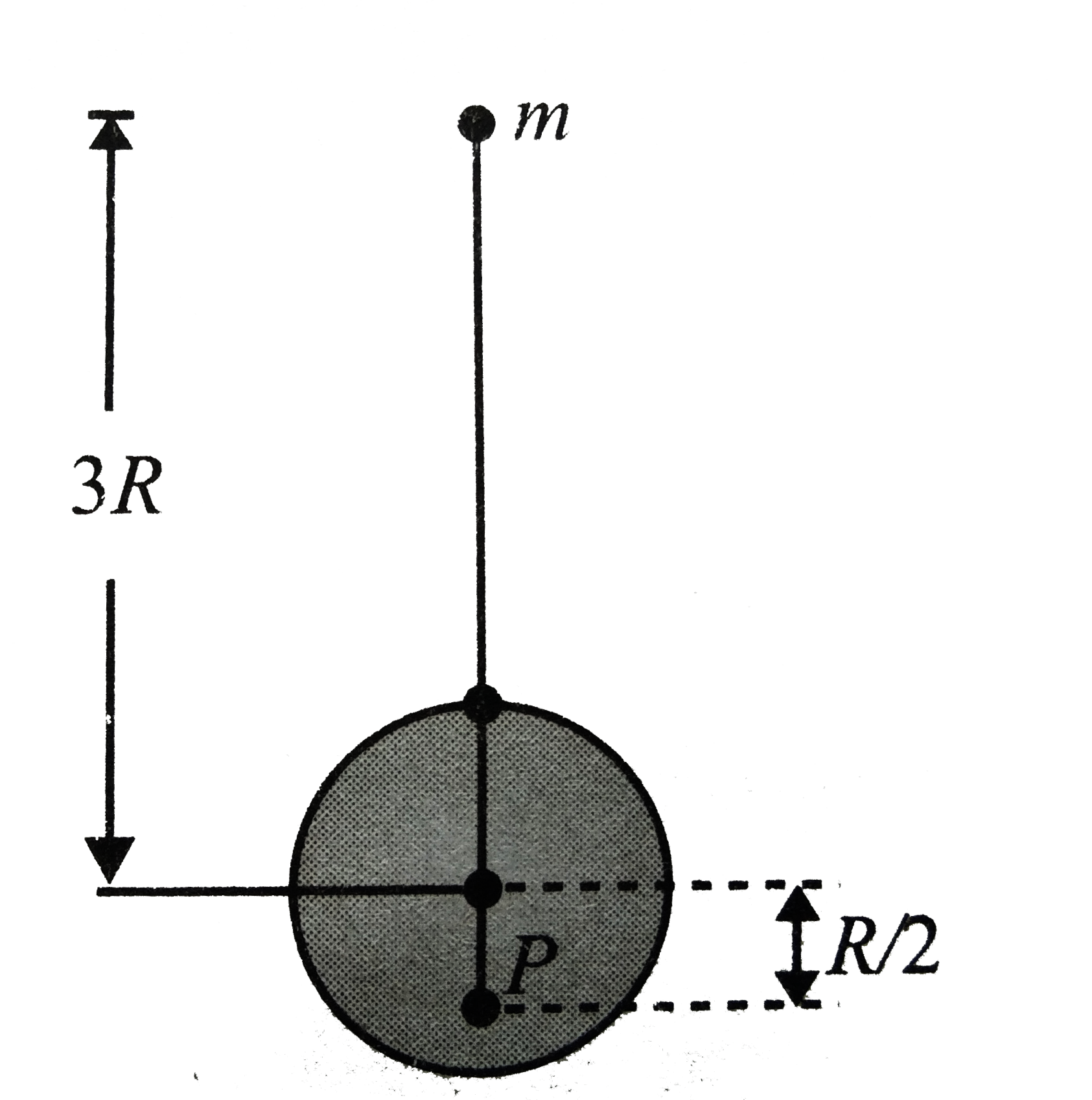
View Solution

