A ring attached with a spring is fitted in a smooth rod. The spring is fixed at the outer end of the ord. The mass of the ring is 3kg& spring constant is 300N/m. The ring is given a velcoity 'V' towards the outer end of the rod. And the rod is set to be rotating with an angular velcity ω. Then ring will move with constant speed with respect to the rod if :
 Natural length of spring is same as that of length of rod.
Natural length of spring is same as that of length of rod.
angular velocity of rod is increased continuously.
ω=10rad/s
angular velocity of rod is decreased continuously.
constant velocity of ring is not possible.
The correct Answer is:B
For the ring to move in a circle at constant speed the net force on it should be zero. Here spring force will provide the necessar centripetal force.

∴Kx=mxω2
⇒ω=√km=√3003=10rad/sec.Ans
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 48
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 49
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 46
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particleseach of mass M are attached gently to the opposite end of a diameter of the ring. The ring now rotates, with an angular velocityω2. Then the ratiomM is
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View SolutionA metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end and is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
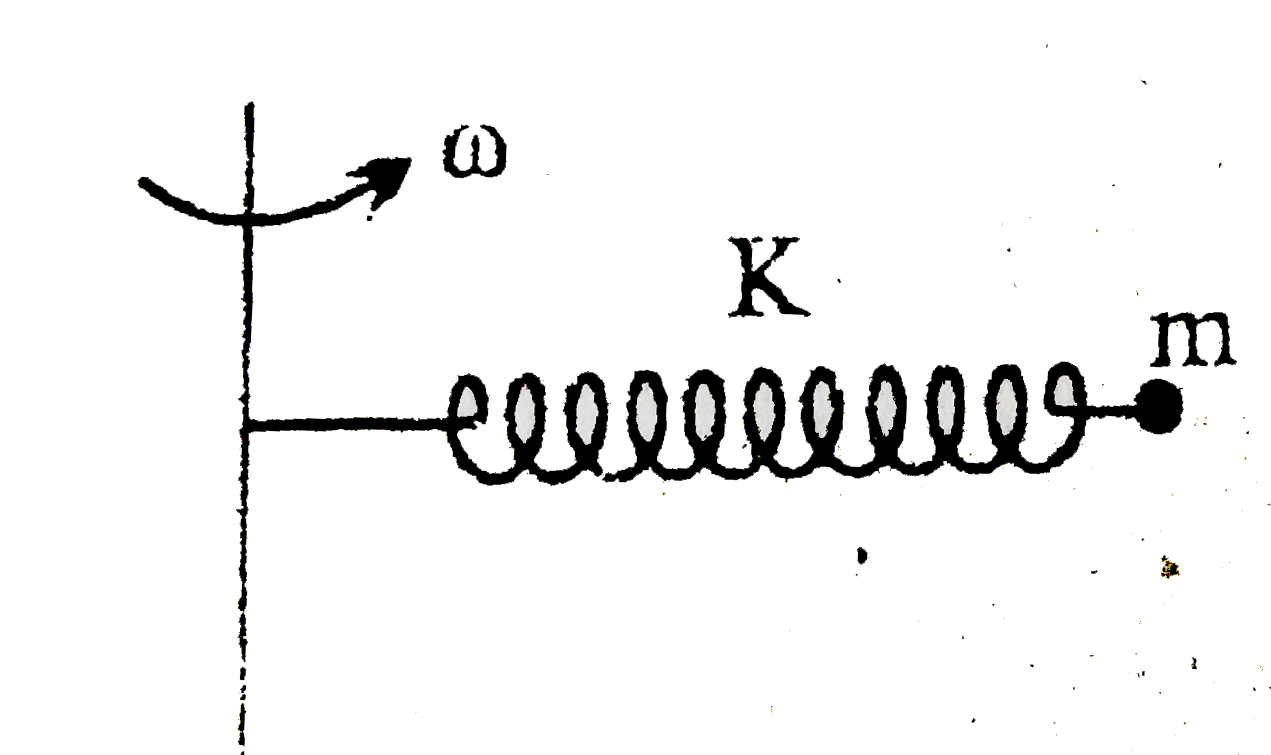
View Solution
