A bead of mass m is attached to one end of a spring of natural length R and spring is fixed at point A on a smooth vertical ring of radius R as shown in figure. The normal reaction at B just after it is released to move is

mg2
√3mg
3√3mg
3√3mg2
The correct Answer is:D
The extension is spring is x=2Rcos30∘−R=(√3−1)R
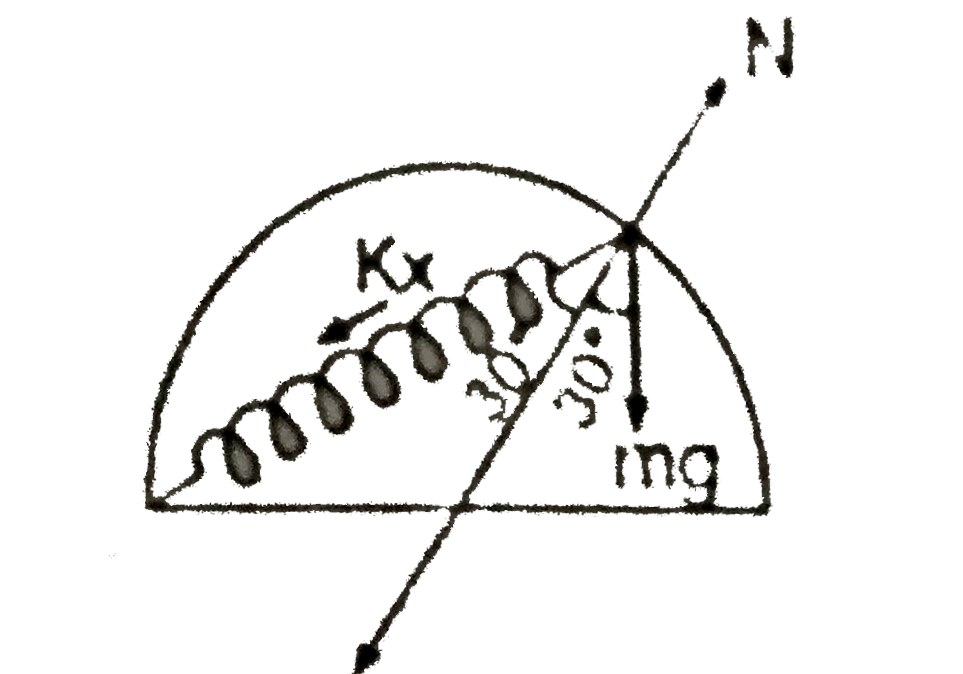
kxcos30∘+mgcos30∘
Applying Newton's second law to the bead normal to circular rind at point B
N=K(√3−1)Rcos30∘+mgcos30∘
=(√3−1)Rmg(√3−1)Rcos30∘+mgcos30∘
N=3√3mg2.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 48
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 49
6 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 46
6 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
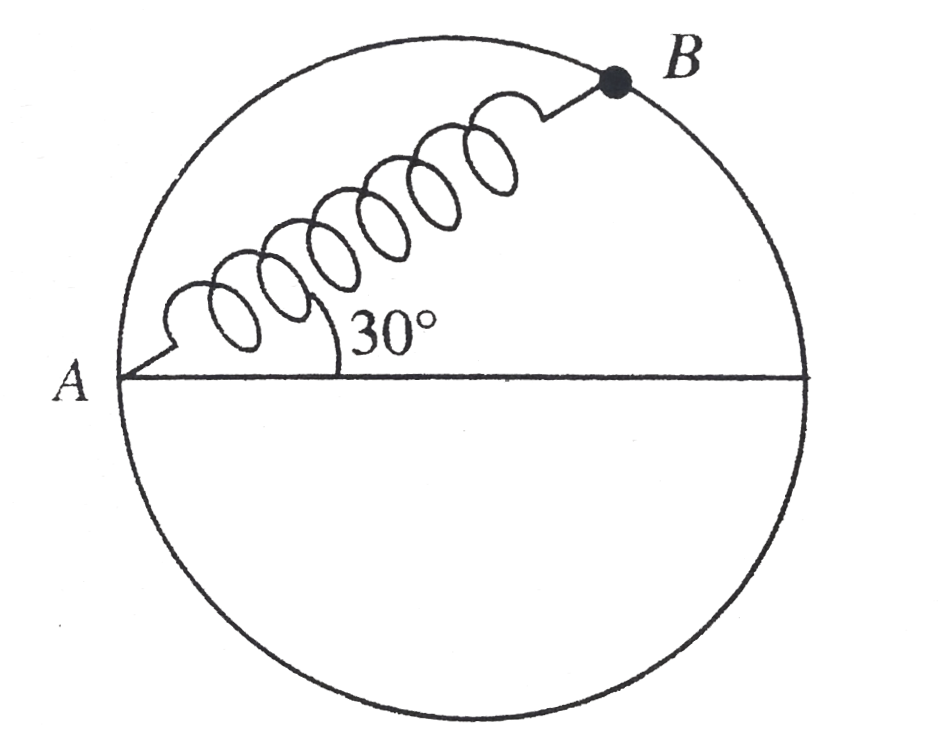
A bead of mass m is attached to one end of a spring of natural length R and spring constant K=(√3+1)mgR. The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
View SolutionA block A of mass m is attached at one end of a light spring and the other end of the spring is connected to another block B of mass 2m through a light string as shown in the figure. A is held and B is in static equilibrium. Now A is released. The acceleration of A just after that instant is a . In the next case, B is held and A is in static equilibrium. Now when B is released, its acceleration immediately after the releas is b . The value of a/b is (pulley, string and the spring are massless).

View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionTwo beads of equal masses m are attached by a string of length √2a and are free to move in a smooth circular ring lying in a vertical plane as shown in figure. Here a is the radius of the ring. Find the tension and acceleration of B just offer the heads are released to move.

View Solution
A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall.The block can slide on a frictionless table as shown in the figure. The natural length of the spring is L0 and it is compressed to one fourth of natural length and the block is released.Find its velocity as a function of its distance (x) from the wall and maximum velocity of the block. The block is not attached to the spring.
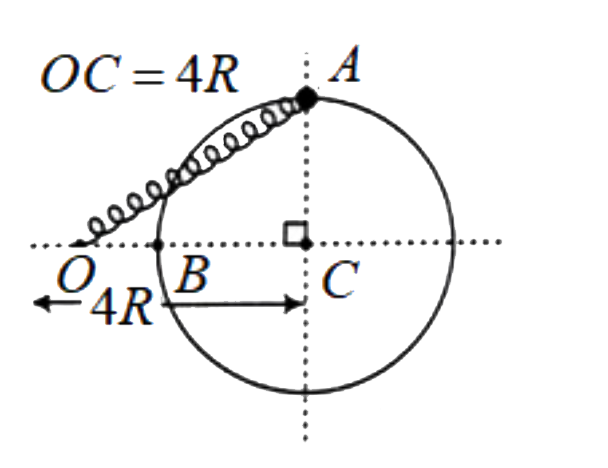
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionA uniform rod of mass m length l is attached to smooth hinge at end A and to a string at end B as shown in figure. It is at rest. The angular acceleration of the rod just after the string is cut is :

View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truck starts moving towards right with a constant accleration a0. As seen from the truck

View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.

View SolutionOn end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).

View Solution
