One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
During circular motion, minimum value of tension in the string−
zero only if m1=m2
mg
10mg
15mg
The correct Answer is:D
To find the minimum value of tension in the string when the ball is performing circular motion, we can follow these steps:
Step 1: Identify the forces acting on the ball at the highest position
At the highest point of the circular motion, the forces acting on the ball are:
- The gravitational force (weight) acting downward, which is mg.
- The tension in the string, which also acts downward at this point.
Step 2: Apply the centripetal force equation
At the highest point, the net force acting towards the center of the circular path must equal the centripetal force required to keep the ball moving in a circle. Therefore, we can write:
T+mg=mv2L
where T is the tension in the string, m is the mass of the ball, v is the velocity at the highest point, and L is the length of the string.
Step 3: Use conservation of energy to find the velocity at the highest point
Using the conservation of mechanical energy, we can relate the kinetic energy at the lowest point to the potential energy at the highest point:
- At the lowest point, the potential energy is 0, and the kinetic energy is 12mu2, where u=√20gl.
- At the highest point, the potential energy is mg(2L) (since the height is 2L), and the kinetic energy is 12mv2.
Setting the total energy at the lowest point equal to the total energy at the highest point:
12mu2=mg(2L)+12mv2
Substituting u2=20gl:
12m(20gl)=mg(2L)+12mv2
Dividing through by m and simplifying:
10gl=2gL+12v2
Rearranging gives:
12v2=10gl−2gL
v2=20gl−4gL
v2=4g(5l−L)
Step 4: Substitute v2 back into the centripetal force equation
Now we substitute v2 into the centripetal force equation:
T+mg=m(4g(5l−L))L
This simplifies to:
T=4mg(5l−L)L−mg
Factoring out mg:
T=mg(4(5l−L)L−1)
Step 5: Find the minimum tension
To find the minimum tension, we evaluate T at the highest point where L=l:
T=mg(4(5l−l)l−1)
T=mg(4(4l)l−1)
T=mg(16−1)=15mg
Thus, the minimum value of tension in the string is:
15mg
At the highest point of the circular motion, the forces acting on the ball are:
- The gravitational force (weight) acting downward, which is mg.
- The tension in the string, which also acts downward at this point.
At the highest point, the net force acting towards the center of the circular path must equal the centripetal force required to keep the ball moving in a circle. Therefore, we can write:
T+mg=mv2L
where T is the tension in the string, m is the mass of the ball, v is the velocity at the highest point, and L is the length of the string.
Using the conservation of mechanical energy, we can relate the kinetic energy at the lowest point to the potential energy at the highest point:
- At the lowest point, the potential energy is 0, and the kinetic energy is 12mu2, where u=√20gl.
- At the highest point, the potential energy is mg(2L) (since the height is 2L), and the kinetic energy is 12mv2.
12mu2=mg(2L)+12mv2
Substituting u2=20gl:
12m(20gl)=mg(2L)+12mv2
Dividing through by m and simplifying:
10gl=2gL+12v2
Rearranging gives:
12v2=10gl−2gL
v2=20gl−4gL
v2=4g(5l−L)
Now we substitute v2 into the centripetal force equation:
T+mg=m(4g(5l−L))L
This simplifies to:
T=4mg(5l−L)L−mg
Factoring out mg:
T=mg(4(5l−L)L−1)
To find the minimum tension, we evaluate T at the highest point where L=l:
T=mg(4(5l−l)l−1)
T=mg(4(4l)l−1)
T=mg(16−1)=15mg
15mg
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
Motion of ball is in nature of
View SolutionOne end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
At the highest position of ball, tangential acceleration of ball is −
View Solution
Knowledge Check
One end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
ATBT−(mv)2lCT+mv2lD0
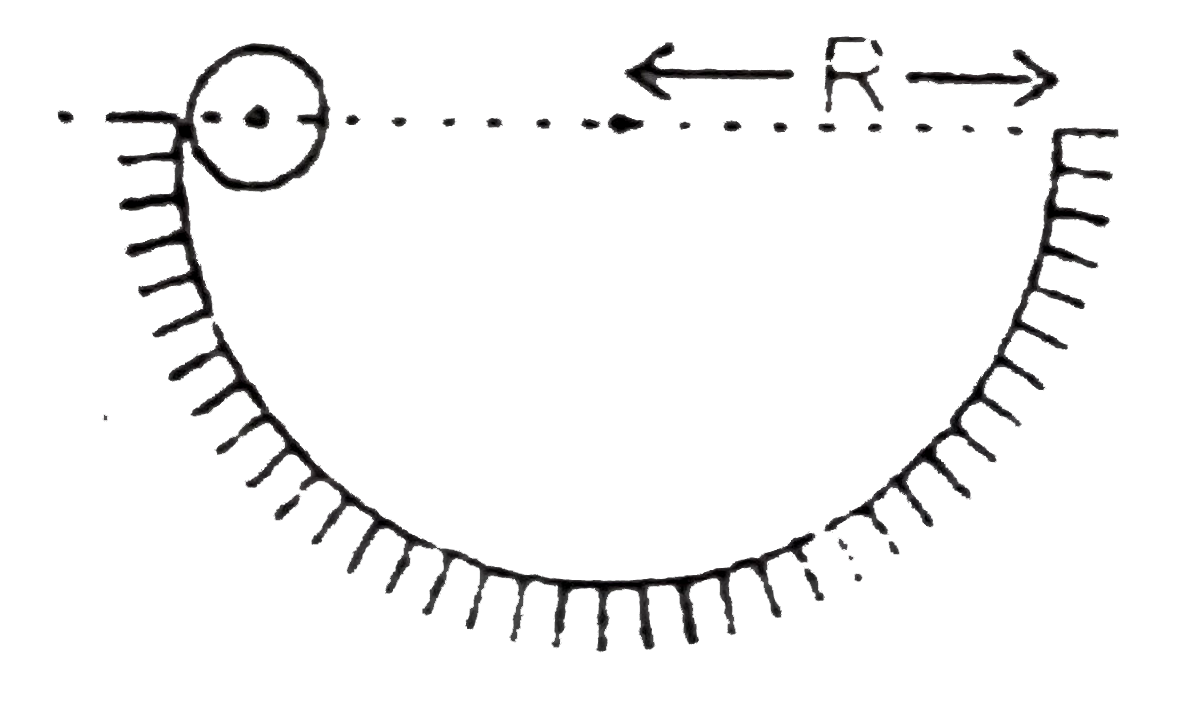
In the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
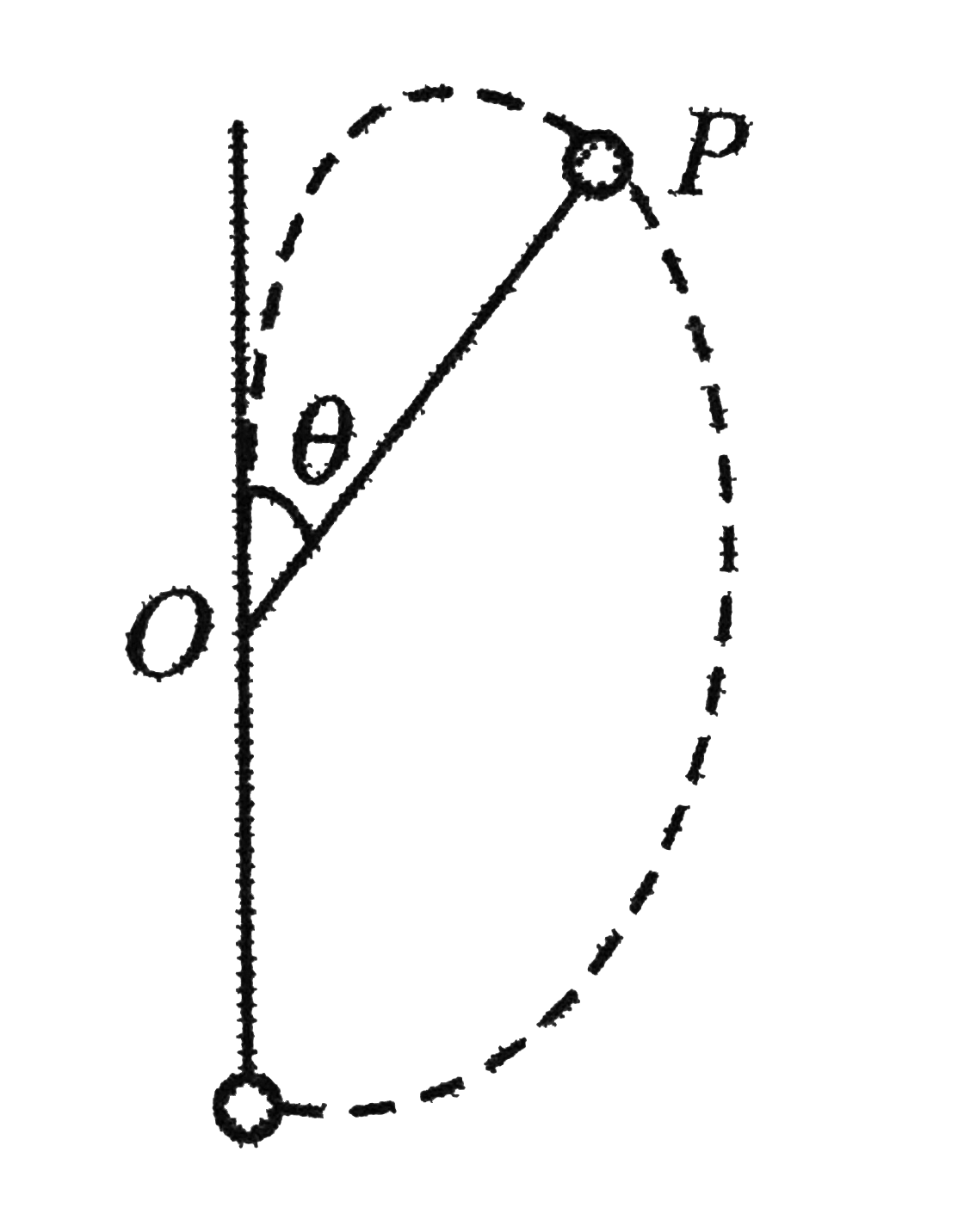
View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
View SolutionOne end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
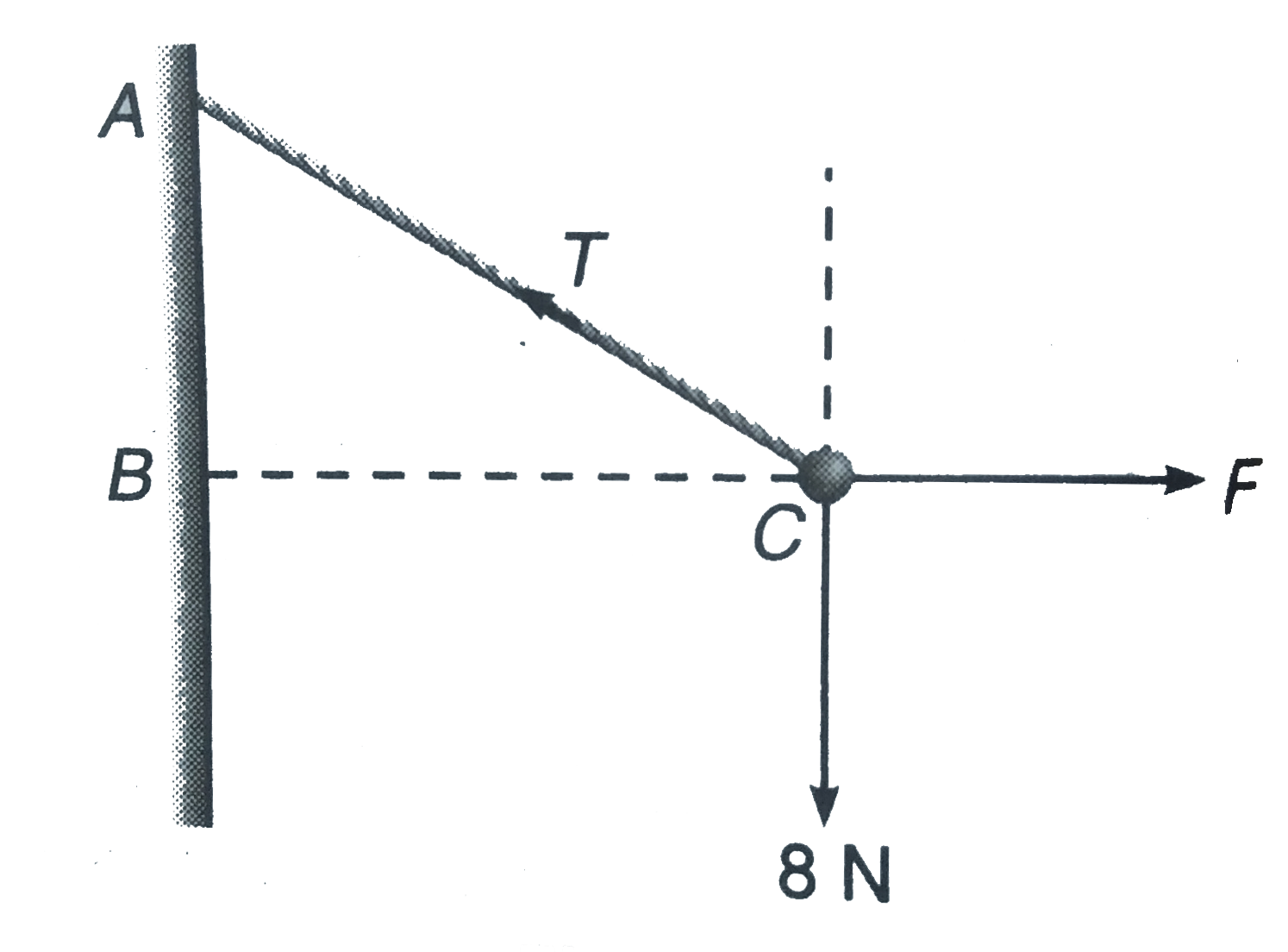
View SolutionOne end of a string 0.5m long is fixed to a point A and the other end is fastened to a small object of weight 8N. The object is pulled aside by a horizontal force F, until it is0.3m from the vertical through A.Find the magnitude of the tension T in the string and force F.
View Solution
