One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
Motion of ball is in nature of
circular motion with constant speed
circular motion with variable speed
circular motion with constant angular acceleration about centre of the circle.
none of these
The correct Answer is:B
To determine the nature of the motion of the ball tied to a massless inextensible string performing circular motion in a vertical plane, we can analyze the situation step by step.
Step 1: Understanding the System
The ball is tied to a string of length l and is performing circular motion in a vertical plane. At the lowest point of the motion, the speed of the ball is given as v=√20gl.
Step 2: Analyzing Forces at the Lowest Point
At the lowest point of the circular path, two forces act on the ball:
1. The gravitational force mg acting downward.
2. The tension T in the string acting upward.
The net force acting towards the center of the circular path is the difference between the tension and the weight of the ball:
Fnet=T−mg
Step 3: Applying Newton's Second Law
According to Newton's second law, the net force is also equal to the mass times the centripetal acceleration:
Fnet=m⋅ac
where ac=v2l is the centripetal acceleration.
Setting the two expressions for the net force equal gives:
T−mg=m⋅v2l
Step 4: Substituting the Given Speed
Substituting v=√20gl into the equation:
T−mg=m⋅(√20gl)2l
T−mg=m⋅20gll
T−mg=20mg
T=21mg
Step 5: Analyzing the Motion
Since the speed of the ball changes as it moves along the circular path (it is maximum at the lowest point and decreases as it rises), we can conclude that:
1. The speed of the ball is not constant; it varies as the ball moves through the vertical circle.
2. The ball is undergoing circular motion with variable speed.
Step 6: Considering Angular Acceleration
The ball is also experiencing a change in direction, which implies that there is angular acceleration involved. However, since the tangential speed is changing, we can conclude that there is a non-zero tangential acceleration.
Conclusion
The nature of the motion of the ball is:
- Circular motion with variable speed.
- Circular motion with constant angular acceleration about the center of the circle.
The ball is tied to a string of length l and is performing circular motion in a vertical plane. At the lowest point of the motion, the speed of the ball is given as v=√20gl.
At the lowest point of the circular path, two forces act on the ball:
1. The gravitational force mg acting downward.
2. The tension T in the string acting upward.
Fnet=T−mg
According to Newton's second law, the net force is also equal to the mass times the centripetal acceleration:
Fnet=m⋅ac
where ac=v2l is the centripetal acceleration.
T−mg=m⋅v2l
Substituting v=√20gl into the equation:
T−mg=m⋅(√20gl)2l
T−mg=m⋅20gll
T−mg=20mg
T=21mg
Since the speed of the ball changes as it moves along the circular path (it is maximum at the lowest point and decreases as it rises), we can conclude that:
1. The speed of the ball is not constant; it varies as the ball moves through the vertical circle.
2. The ball is undergoing circular motion with variable speed.
The ball is also experiencing a change in direction, which implies that there is angular acceleration involved. However, since the tangential speed is changing, we can conclude that there is a non-zero tangential acceleration.
The nature of the motion of the ball is:
- Circular motion with variable speed.
- Circular motion with constant angular acceleration about the center of the circle.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
One end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
At the highest position of ball, tangential acceleration of ball is −
View SolutionOne end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
During circular motion, minimum value of tension in the string−
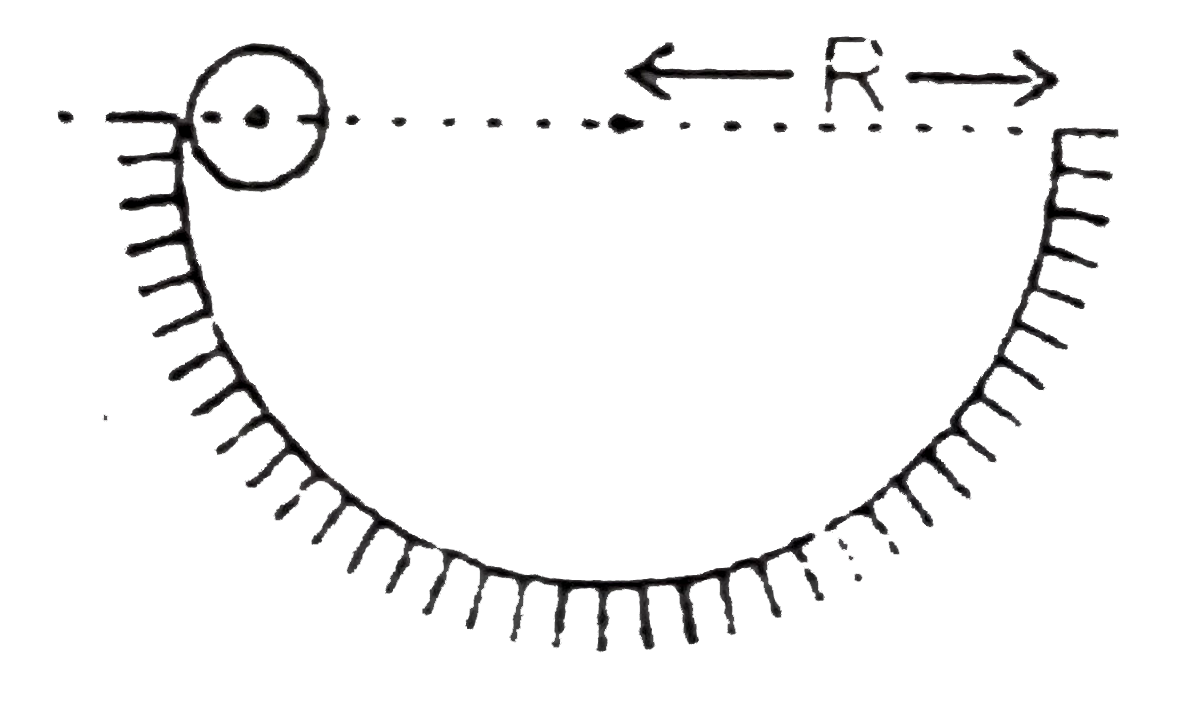
View SolutionIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
View SolutionA particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
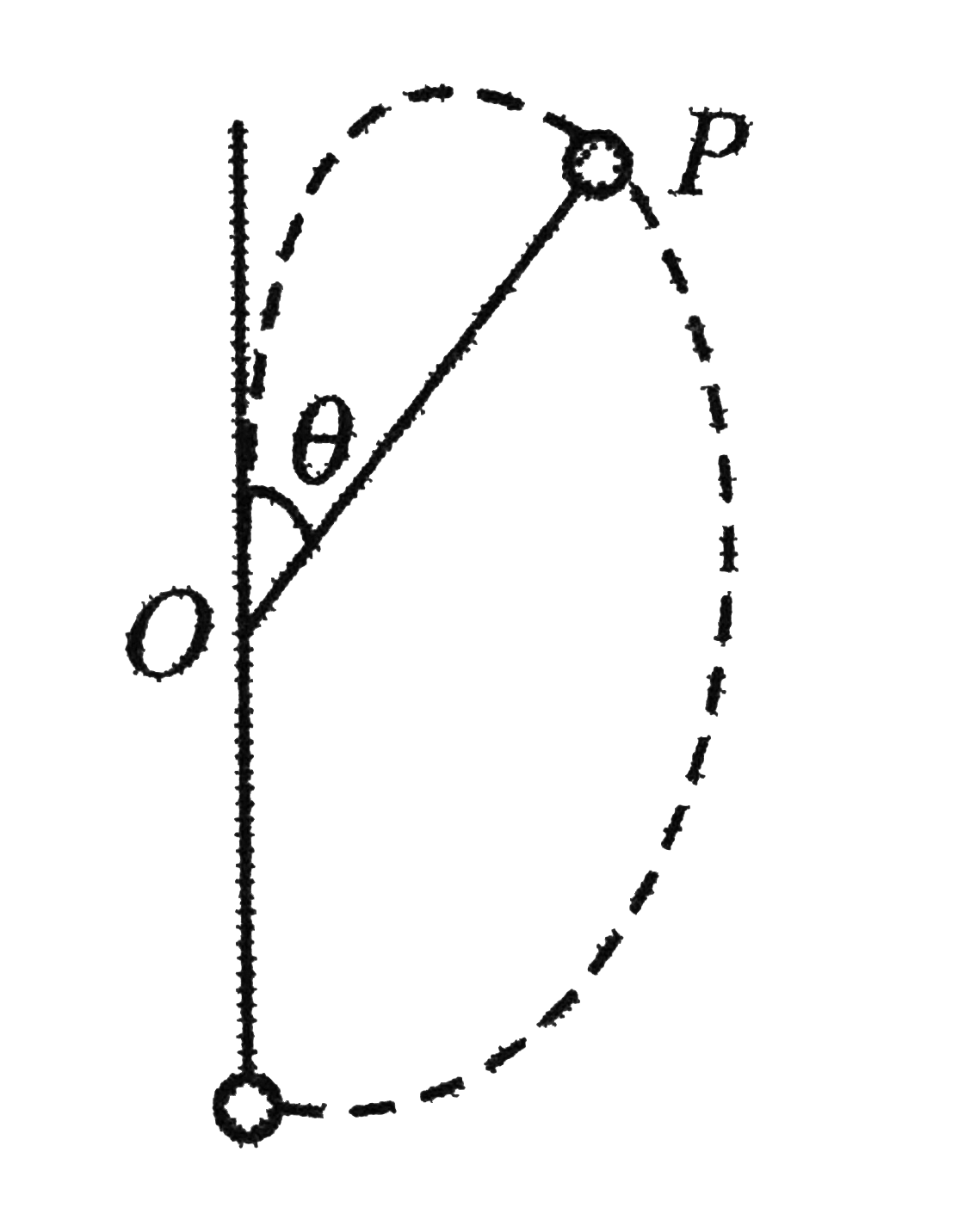
View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
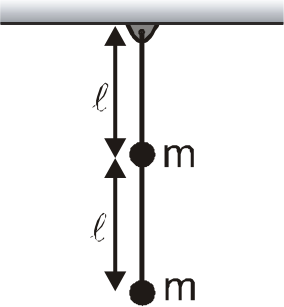
View SolutionTwo particle of mass m each are fixed to a massless rod of length 2l . The rod is hinged at one end about a smooth hinge and it performs oscillations of small angle in vertical plane. The length of the equivalent simple pendulum is:
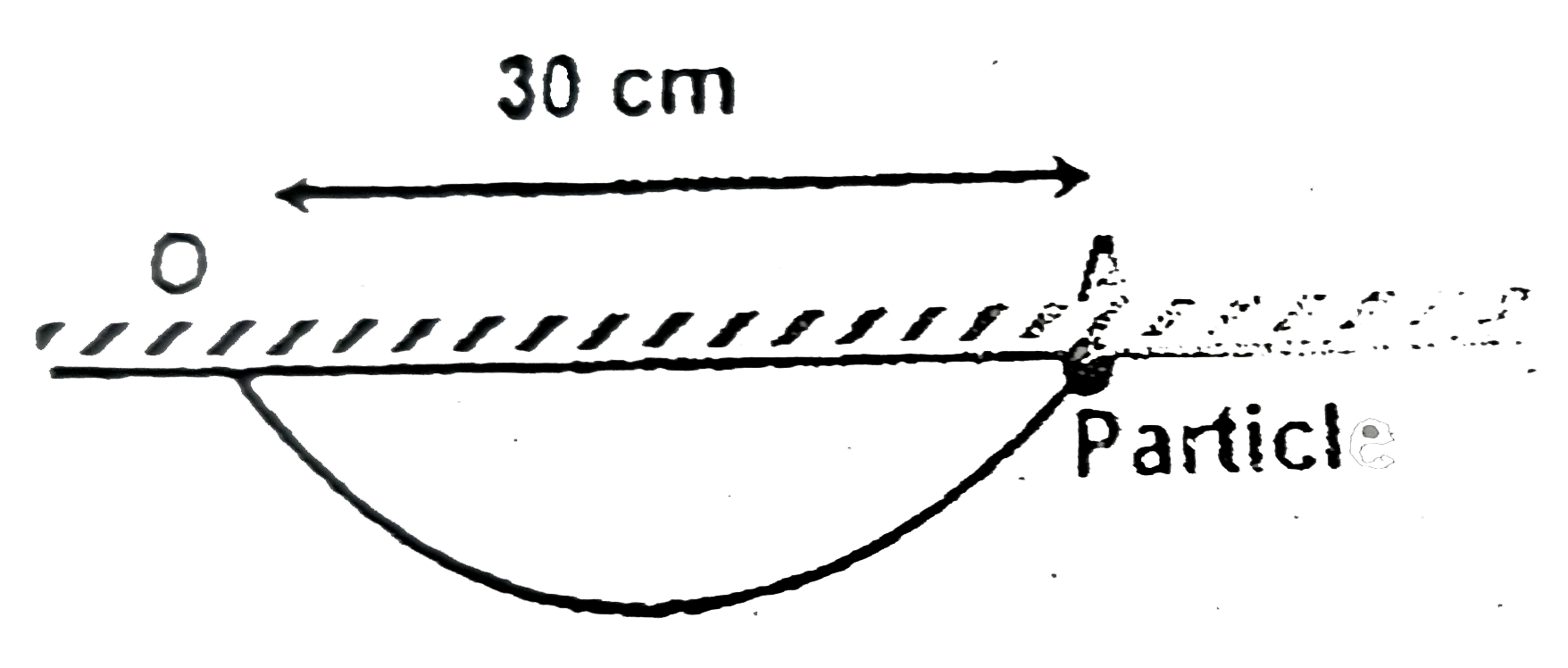
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionOne end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.
If |→vC=2|→vB∣ then the value of θ as shown is
View SolutionOne end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA stone is tied to one end of a light inexensible string of length l and made to roate on a vertical circle keeping other end of the spring at the centre. If speed of stone at the highest point is v(v>√gl) then its speed at the lowest point is
View Solution
