A smooth rope of mas m and length L lies in a heap on a smooth horizontal floor, with one end attached to a block of mass M. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude V0 as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance x from point P as shown in figure −2(P is a point on the rope which has just started to move at the given instant ), choose correct options for next three question.

The speed of block of mass M is
m3LV20(M+mLx)3
mM2LV20(M+mLx)3
m4MLV20(M+mLx)3
M2LV20(M+mLx)3
The correct Answer is:B
The mass of moving material is M+mLx
From conservation of momentum MV0=(M+mLx)V
∴Velocity of moving block and moving rope is
V=MV0M+mLx
(B) The acceleration of moving block is
a=−vdvdx=−MV0(M+mLx)2×mLdxdt
=−mLM2V20(M+mLx)3
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 70
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 71
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 69
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
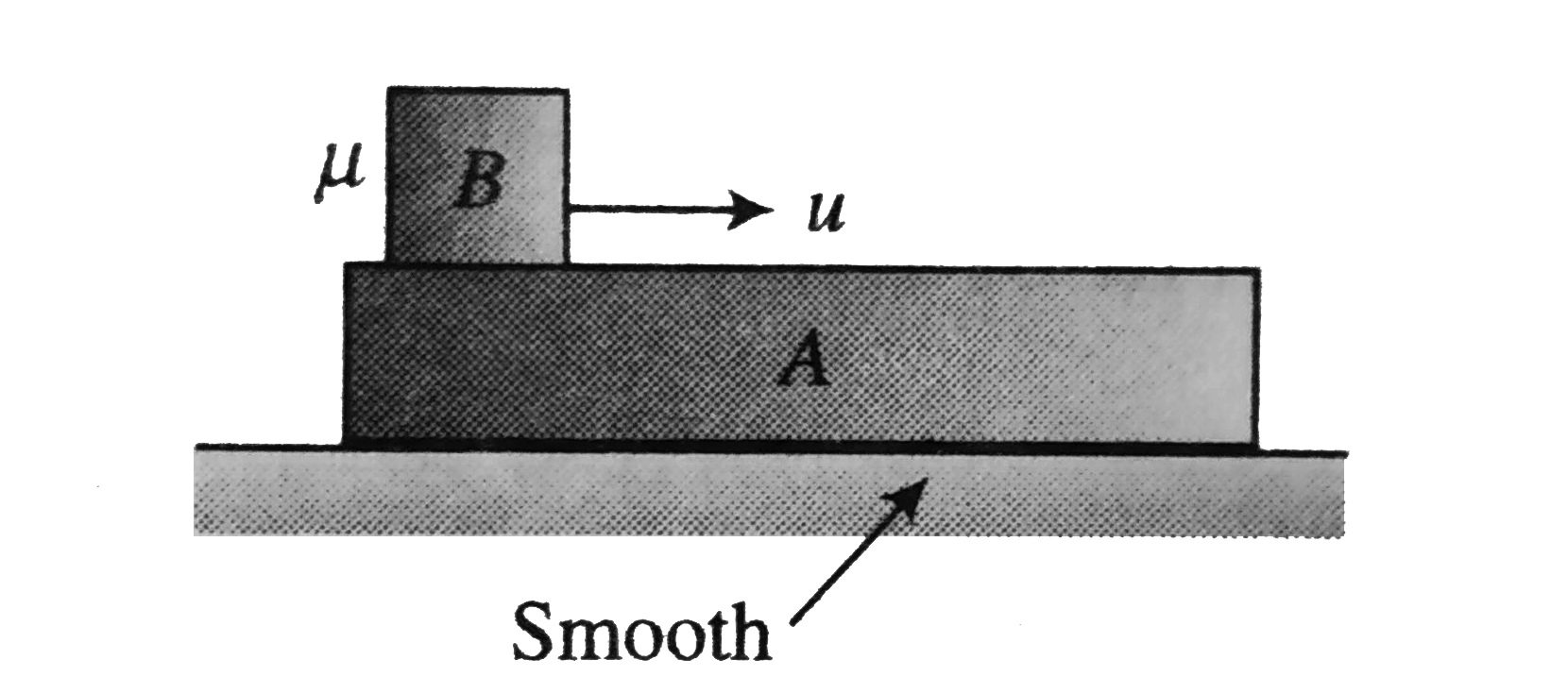
A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
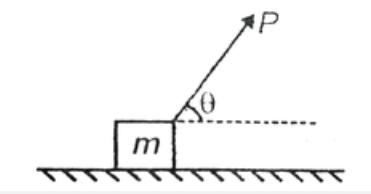
View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block
View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

View SolutionA rope of length 10m and linear density 0.5kg/m is lying length wise on a smooth horizontal floor It is pulled by a force of 25N. The tension in the rope at a point 6m away from the point of application is .
View SolutionA block is dragged on a smooth plane with the help of a rope which moves with a velocity v as shown in figure. The horizontal velocity of the block is :

View SolutionA block of mass of 20kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in figure.Find the acceleration of the pulley
_PHY_E05_034_Q01.png) .jpg
.jpg
View SolutionA block of mass 20 kg is set into motion on a frictionless horizontal surface with the help of massless smooth pulley and rope as shown in the figure. Find the acceleration of the pulley
_PHY_E05_192_Q05.png)
View SolutionA block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
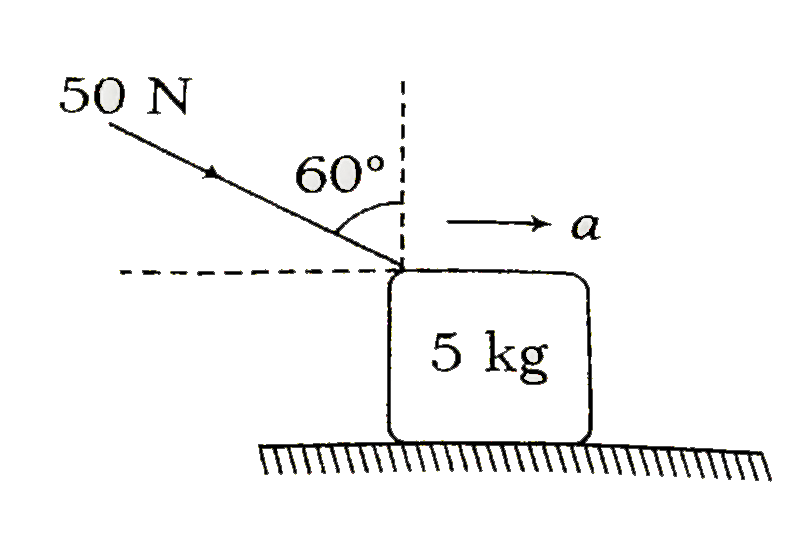
View SolutionA force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.

View Solution
