Uniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.
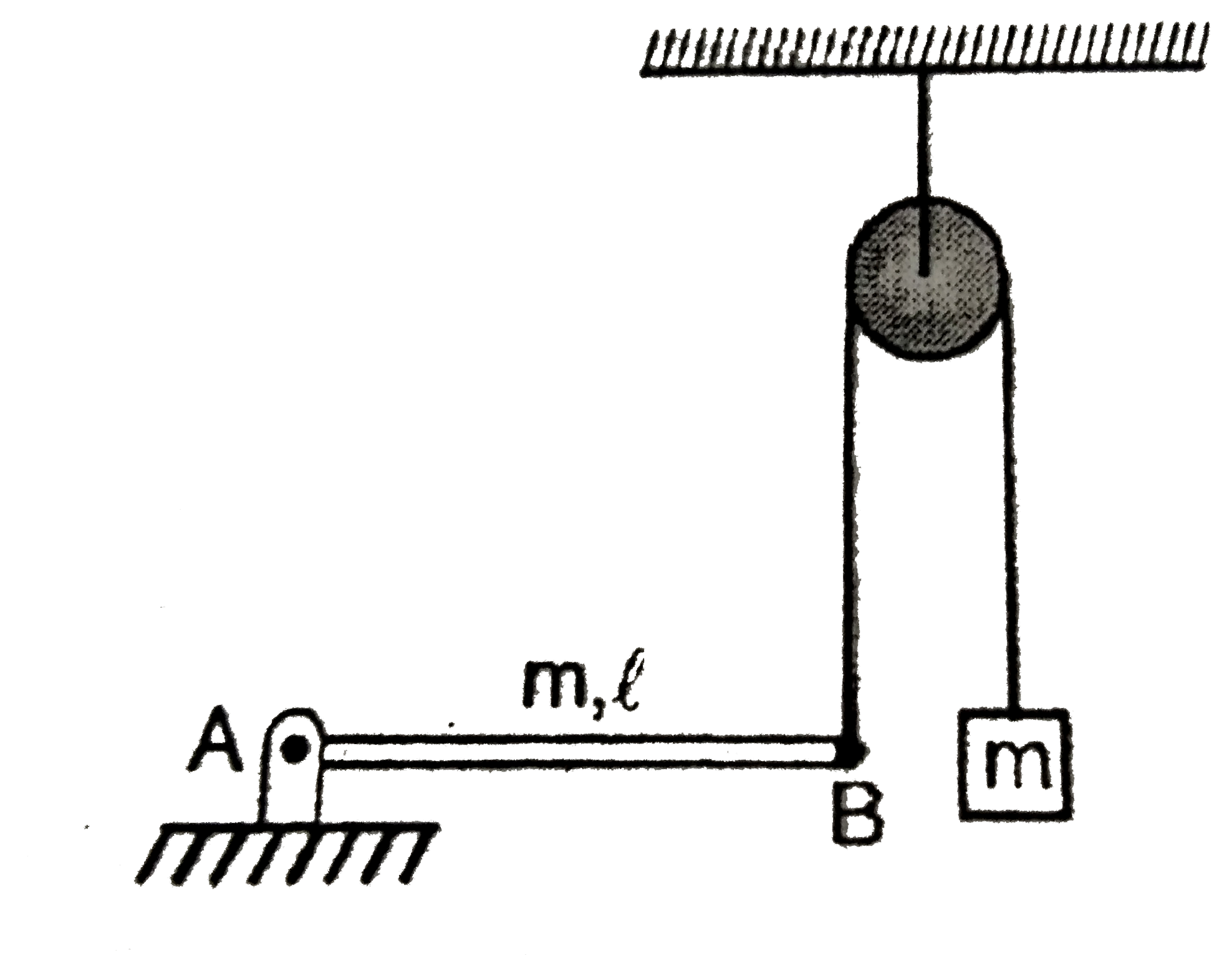
Then just after released of block from this position, the angular acceleration of the rod is
g8l
5g8l
11g8l
3g8l
The correct Answer is:D
Let α be the angular acceleration of rod and a be acceleration of block just after its release.
∴Mg−T=ma…….(1)
Tl=mgl2=ml23α....(2)
and a=lα….(3)
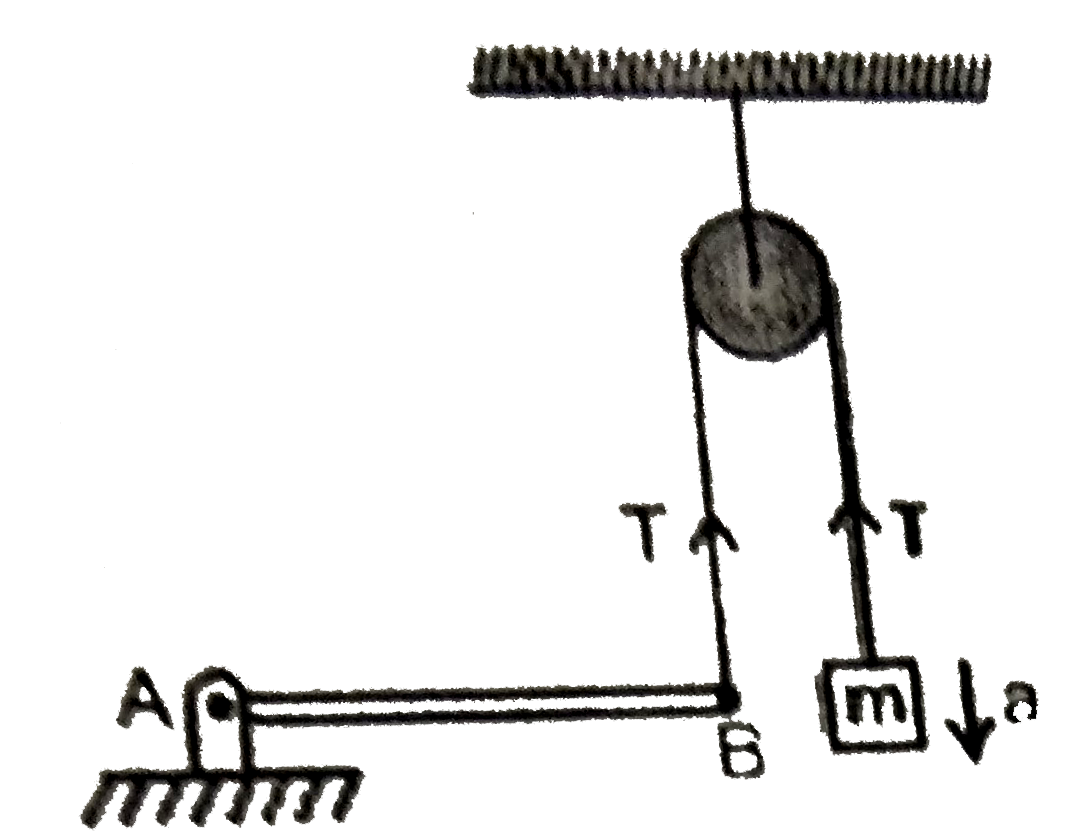
Solving we get
T=5mg8and α=3g8l
Now from free body diagram of rod, let R be the reaction by hinge on rod.
R+T−mg=macm=m12α

Solving we get R=9mg16
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Uniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.
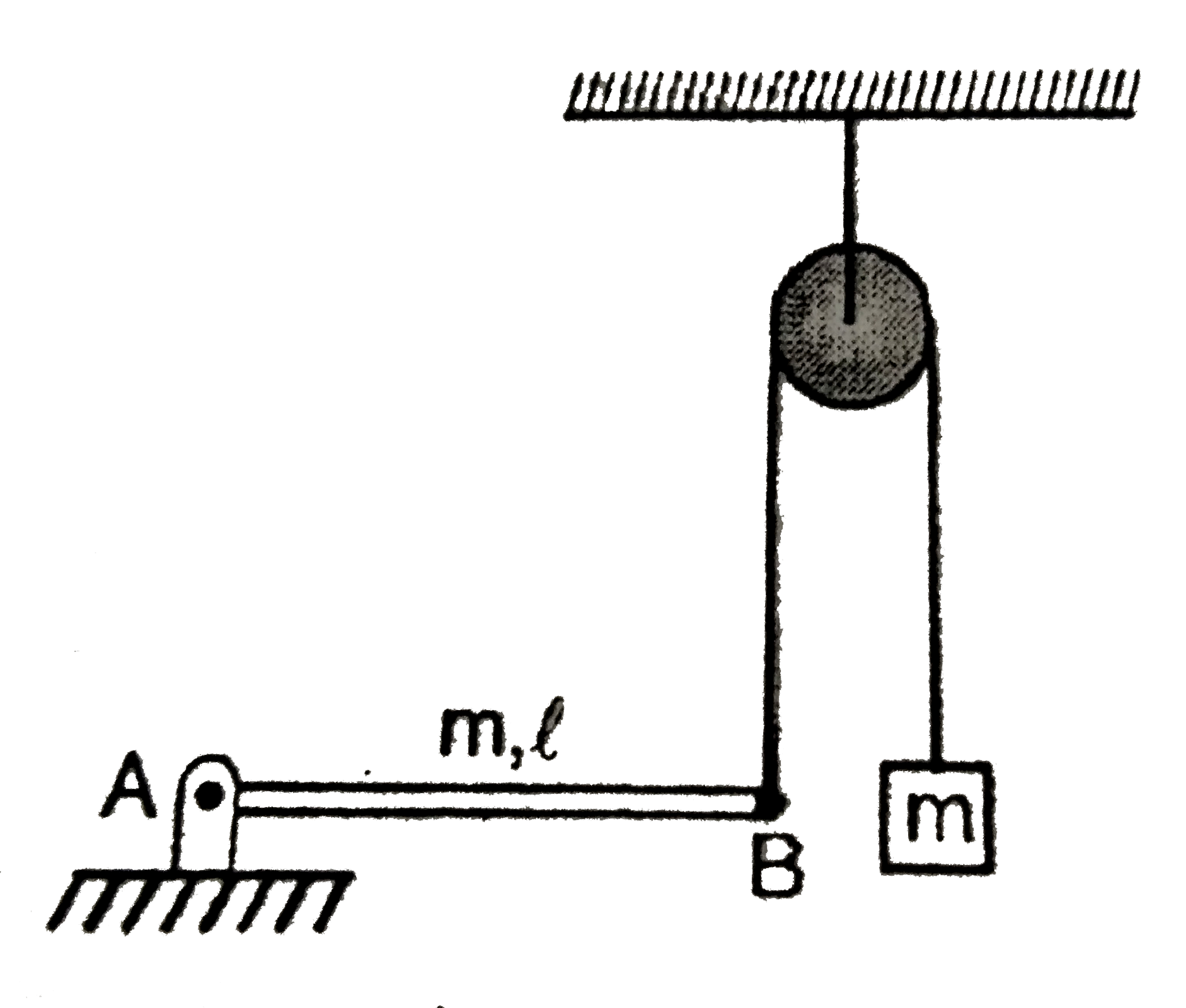
Then just after release of block from this position, the tension in the thread is
View SolutionUniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.

Then just after release of block from this position, the magnitude of reaction exerted by hinge on the rod is
View Solution
Uniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to m Then acceleration of block just after release from this position is
View SolutionUniform rod AB is hinged at the end A in the figure. The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are

View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
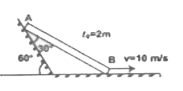
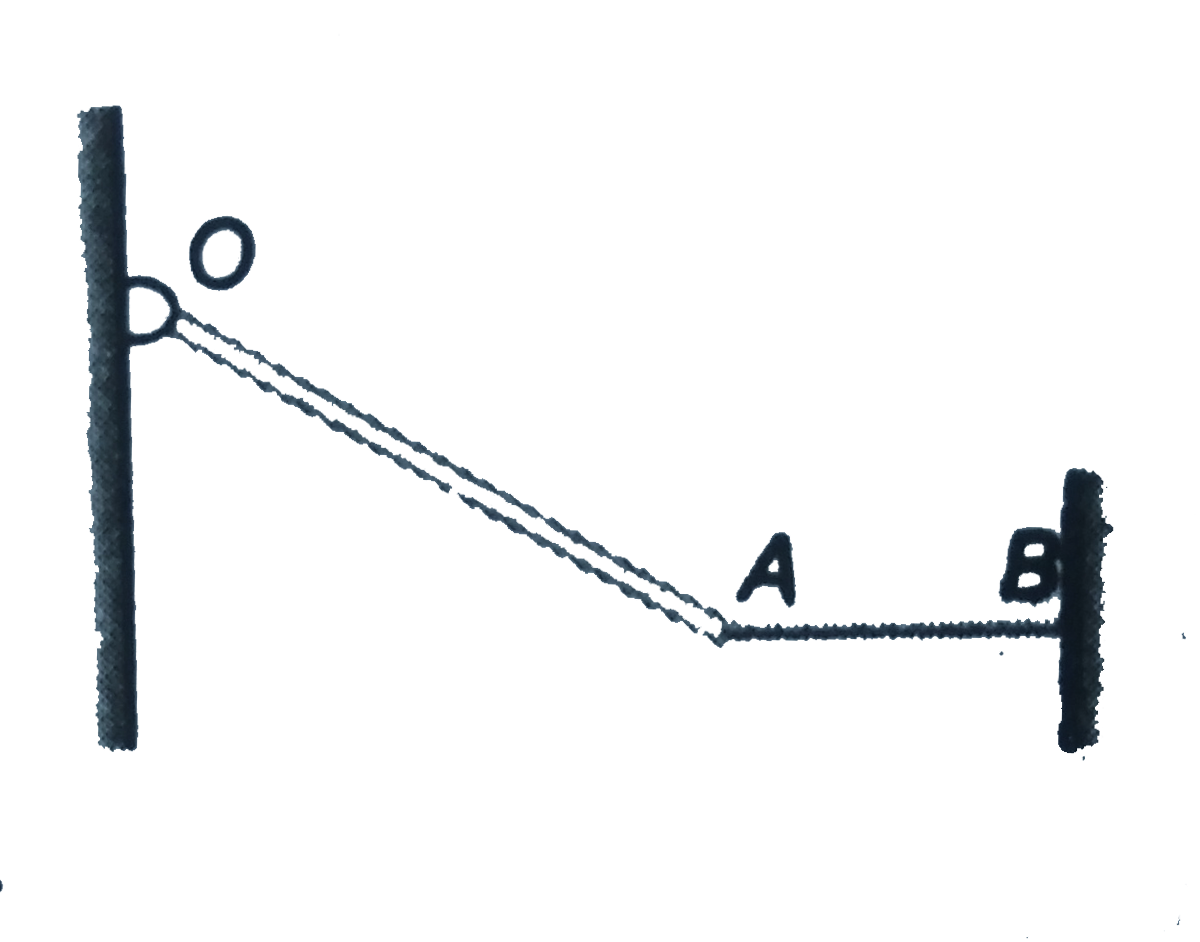
View SolutionA rod OA is suspended with the help of a massless string AB as shown in figure. Rod is hinged at pointO. Draw free body diagrame of the rod.
View Solution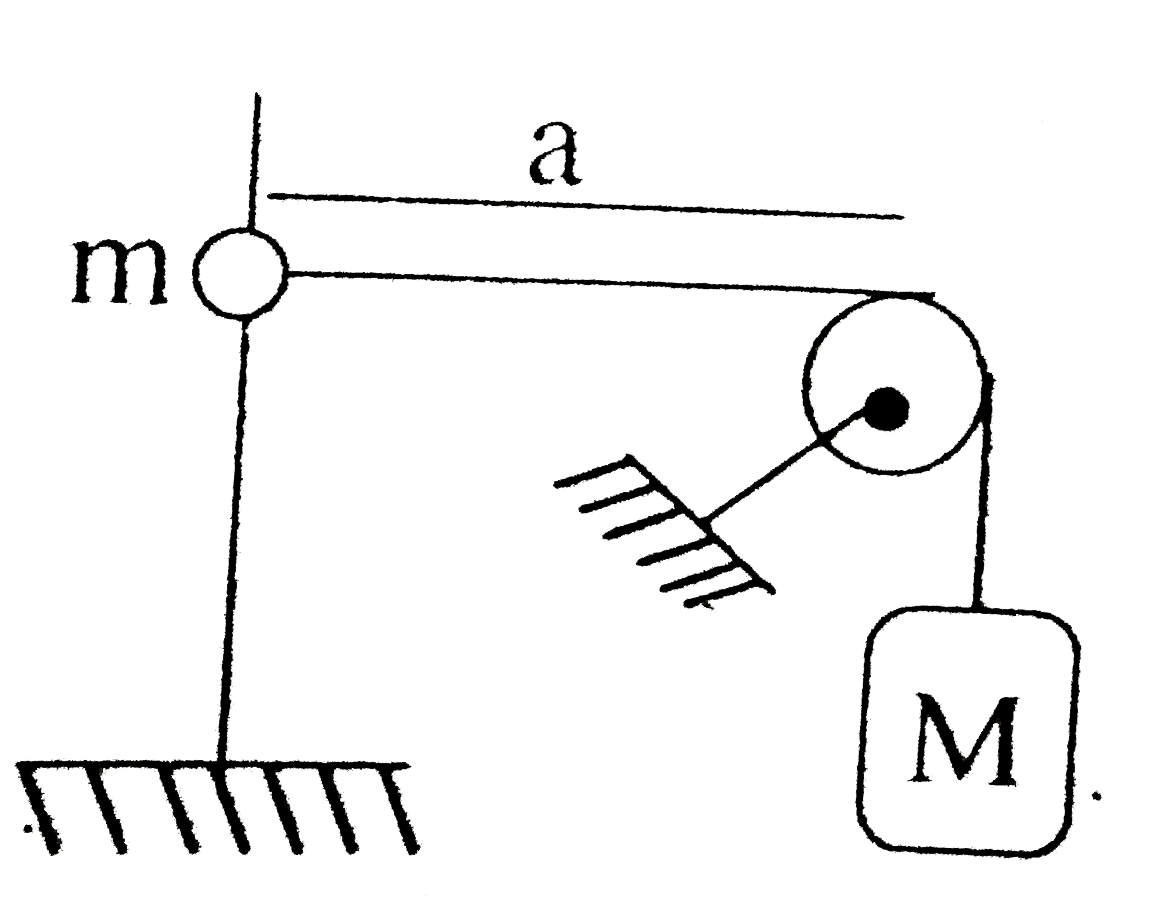
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from the rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes verticle is

View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.

View SolutionA uniform rod of mass m, hinged at its upper end, is released from rest from a horizontal position. When it passes through the vertical position, the force on the hinge is
View Solution
