A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The magnitude of normal reaction exerted by the rod on the cylinder is
mg4
mg3
mg2
2mg3
The correct Answer is:C
FBD of rod and cylinder is as shown.
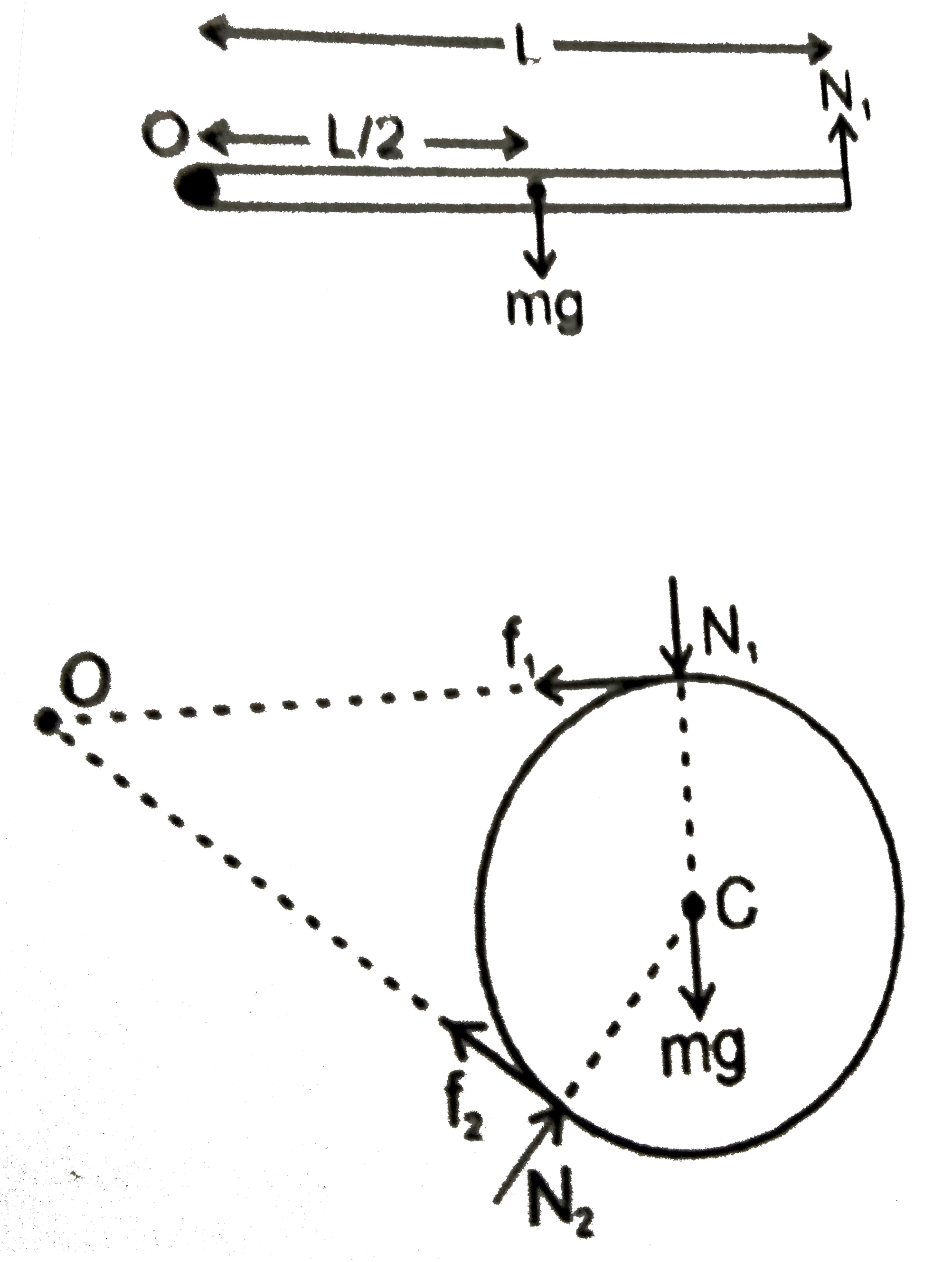
Net torque on rod about hinge 'O'=0
∴N1×L=mg×L2or
N1=mg2
Net torque on cylinder about its centre C is zero :
f1R=f2R orf1=f2
Net torque on cylinder about hinge O is zero.
∴N2×L=N1×L+mgL
or N2= , 3mg2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 70
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 71
8 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 69
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
53 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
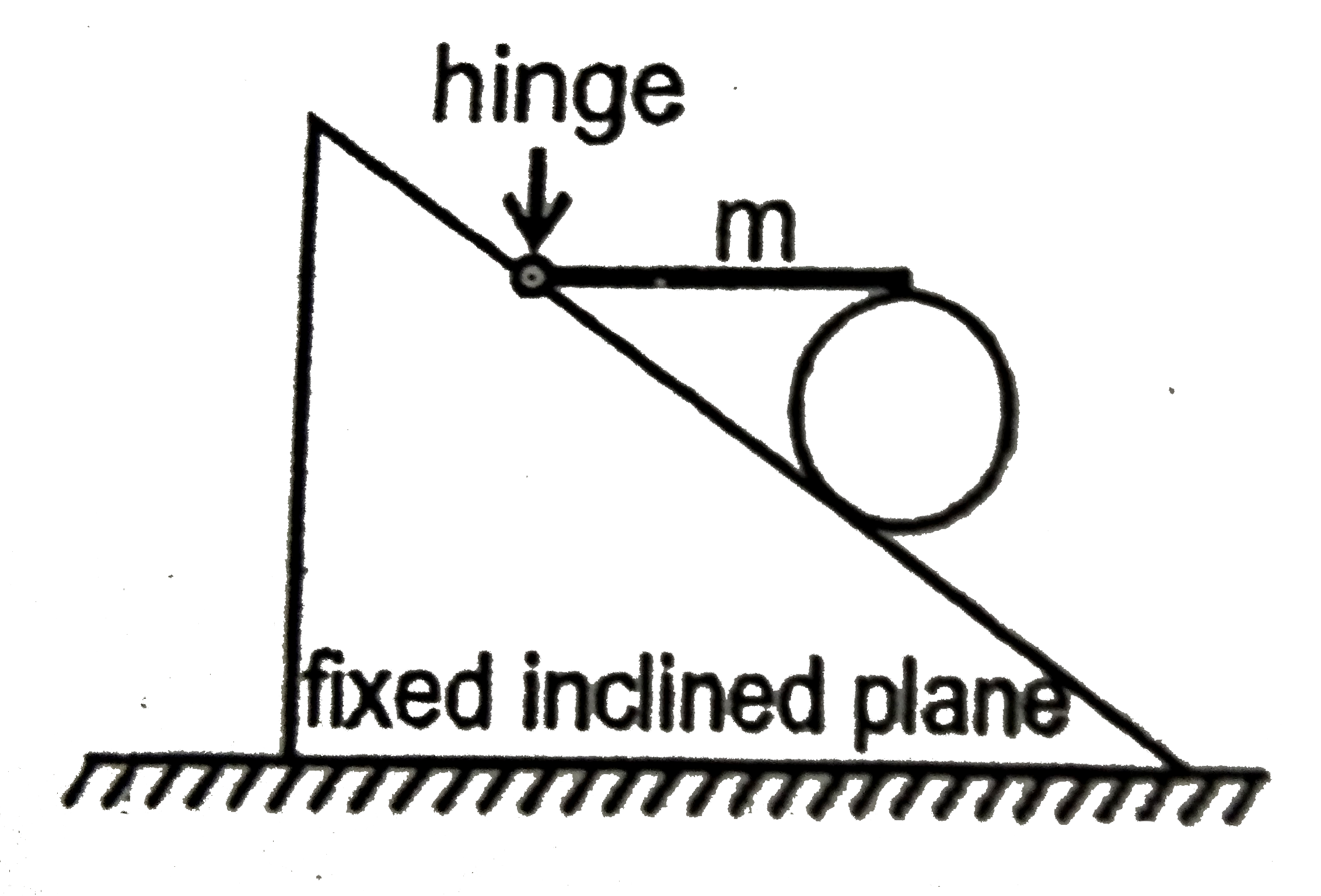
The magnitude of normal reaction exerted by the inclinded plane on the cylinder is :
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.

The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :
View Solution
Knowledge Check
A block of mass m is at rest on an inclined plane. The coefficient of static friction is μ. The maximum angle of incline before the block begins to slide down is :
Atan−1(μ/m)Btan−1(μ)Ctan−1(μ/2)Dcos−1(μ)
A uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is

View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
View SolutionThe two blocks A and B of equal mass are initially in contact when released from rest on the inclined plane. The coefficients of friction between the inclined plane and A and B are μ1 and μ2 respectiely. Friction is not sufficient to prevent slipping.
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionIf a solid cylinder rolls down an inclined plane, then its:
View Solution
