A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u. The tension in the string is T and acceleration of the particle is a at any position then T. a' is positive at the lowest point for
u=√2gl
u=√5gl
u=√7gl
any value of u
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of the particle in a vertical circular path and the relationship between tension (T) and acceleration (a) at the lowest point of the circular motion.
1. Understanding the Setup:
- A particle is attached to a string of length l and moves in a vertical circular path.
- The particle has a velocity u at the lowest point of the circular path.
2. Forces Acting on the Particle:
- At the lowest point, the forces acting on the particle are:
- The tension T in the string acting upwards.
- The weight mg of the particle acting downwards (where m is the mass of the particle and g is the acceleration due to gravity).
3. Applying Newton's Second Law:
- At the lowest point, the net force acting on the particle provides the centripetal force required for circular motion.
- The equation can be written as:
T−mg=mv2l
- Rearranging gives:
T=mg+mv2l
4. Acceleration of the Particle:
- The acceleration a of the particle at the lowest point is the centripetal acceleration, which can be expressed as:
a=u2l
5. Dot Product of Tension and Acceleration:
- The dot product T⋅a is given by:
T⋅a=T⋅a⋅cos(θ)
- At the lowest point, both tension T and acceleration a act in the same direction (upwards), making the angle θ=0∘.
- Therefore, cos(0∘)=1:
T⋅a=T⋅a
6. Conclusion on the Sign of T⋅a:
- Since both T and a are positive quantities at the lowest point, their product T⋅a is also positive.
- Hence, we conclude that T⋅a is positive at the lowest point for any value of u.
Final Answer:
The dot product T⋅a is positive at the lowest point for any value of u.
- A particle is attached to a string of length l and moves in a vertical circular path.
- The particle has a velocity u at the lowest point of the circular path.
- At the lowest point, the forces acting on the particle are:
- The tension T in the string acting upwards.
- The weight mg of the particle acting downwards (where m is the mass of the particle and g is the acceleration due to gravity).
- At the lowest point, the net force acting on the particle provides the centripetal force required for circular motion.
- The equation can be written as:
T−mg=mv2l
- Rearranging gives:
T=mg+mv2l
- The acceleration a of the particle at the lowest point is the centripetal acceleration, which can be expressed as:
a=u2l
- The dot product T⋅a is given by:
T⋅a=T⋅a⋅cos(θ)
- At the lowest point, both tension T and acceleration a act in the same direction (upwards), making the angle θ=0∘.
- Therefore, cos(0∘)=1:
T⋅a=T⋅a
- Since both T and a are positive quantities at the lowest point, their product T⋅a is also positive.
- Hence, we conclude that T⋅a is positive at the lowest point for any value of u.
The dot product T⋅a is positive at the lowest point for any value of u.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is moving in a circular path in the vertical plane. It is attached at one end of a string of length l whose other end is fixed. The velocity at lowest point is u . The tension in the string T and acceleration of the particle is a at any position. Then T.a is zero at highest point if
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
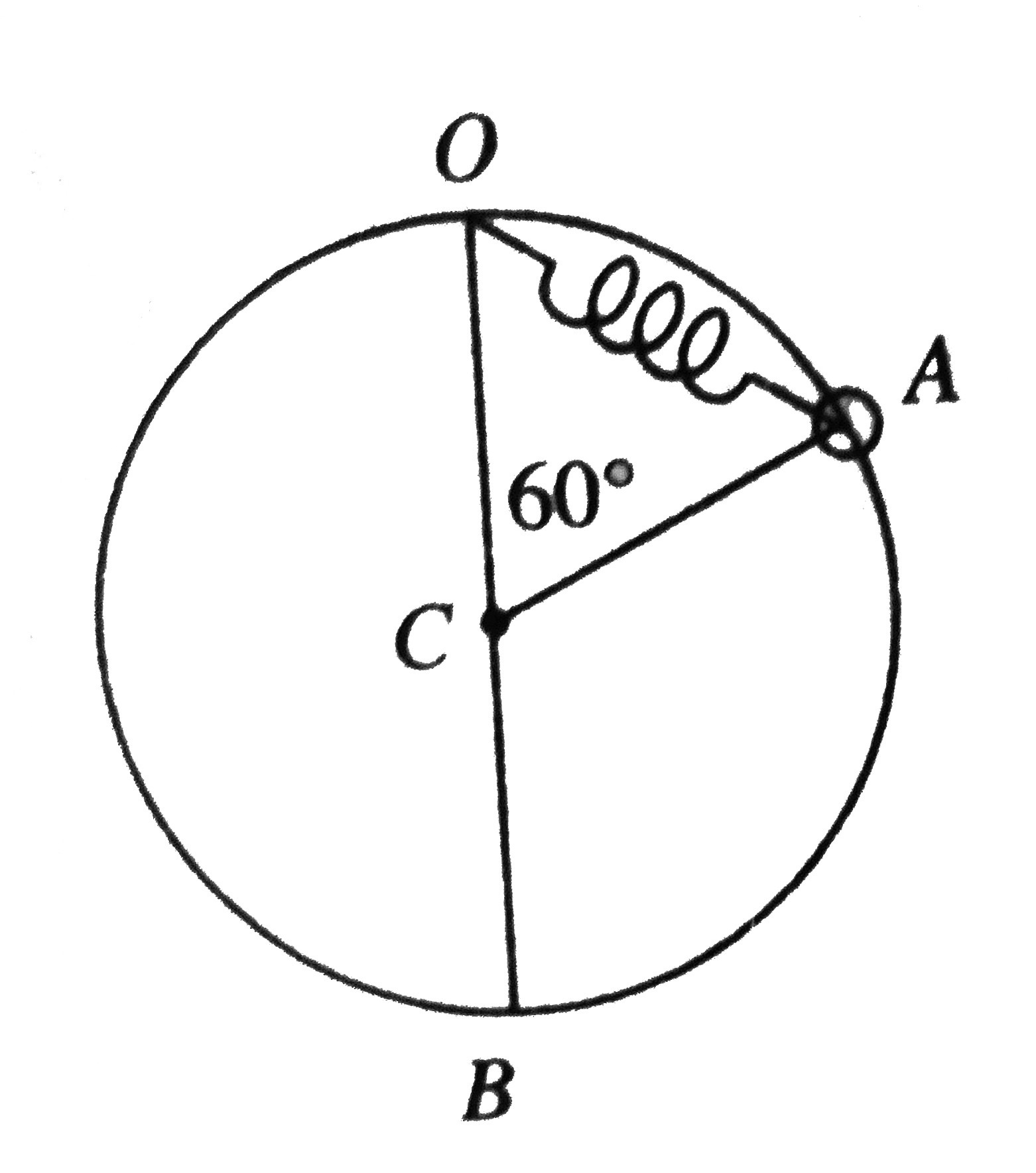
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA particle tied to a string moves in a circular path in vertical plane. Its velocity at lowerst point is such that it just completes circle. Find the ratio of resultant force on particle at the lowerst point to that at highest point.
View Solution
