A dics is rotating in a room. A boy standing near the rim of the disc of radius R finds the water droplet falling from the ceiling is always falling on his head. As one drop hits his head, other one starts from the ceiling. If height of the roof above his head is H , then angular velocity of the disc is
π√2gRH2
π√2gHR2
π√2gH
None of these
The correct Answer is:C
To solve the problem, we need to determine the angular velocity (ω) of a disc that is rotating such that water droplets falling from the ceiling always land on the boy's head standing at the rim of the disc.
1. Understanding the Situation:
- The boy is standing at the rim of a disc of radius R.
- Water droplets fall from the ceiling (height H) and hit the boy's head.
- The time taken for a droplet to fall from the ceiling to the boy's head is denoted as T.
2. Time of Fall:
- The time T for the droplet to fall can be calculated using the equation of motion under gravity:
H=12gT2
- Rearranging this gives:
T2=2Hg
- Taking the square root:
T=√2Hg
3. Relating Time to Angular Velocity:
- The disc makes one complete rotation in time T. The angular velocity ω is given by:
ω=2πT
- Substituting the expression for T:
ω=2π√2Hg
4. Simplifying the Expression:
- We can simplify this expression further:
ω=2π⋅√g2H
- This can be rewritten as:
ω=π⋅√4g2H=π⋅√2gH
5. Final Result:
- Thus, the angular velocity of the disc is:
ω=π√2gH
- The boy is standing at the rim of a disc of radius R.
- Water droplets fall from the ceiling (height H) and hit the boy's head.
- The time taken for a droplet to fall from the ceiling to the boy's head is denoted as T.
- The time T for the droplet to fall can be calculated using the equation of motion under gravity:
H=12gT2
- Rearranging this gives:
T2=2Hg
- Taking the square root:
T=√2Hg
- The disc makes one complete rotation in time T. The angular velocity ω is given by:
ω=2πT
- Substituting the expression for T:
ω=2π√2Hg
- We can simplify this expression further:
ω=2π⋅√g2H
- This can be rewritten as:
ω=π⋅√4g2H=π⋅√2gH
- Thus, the angular velocity of the disc is:
ω=π√2gH
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
If water drops are falling at regular time intervals from ceiling of height H, then position of drop from the ceiling is (when nth drop falling from the ceiling and rth drop is in its way)
View SolutionIn the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.

View Solution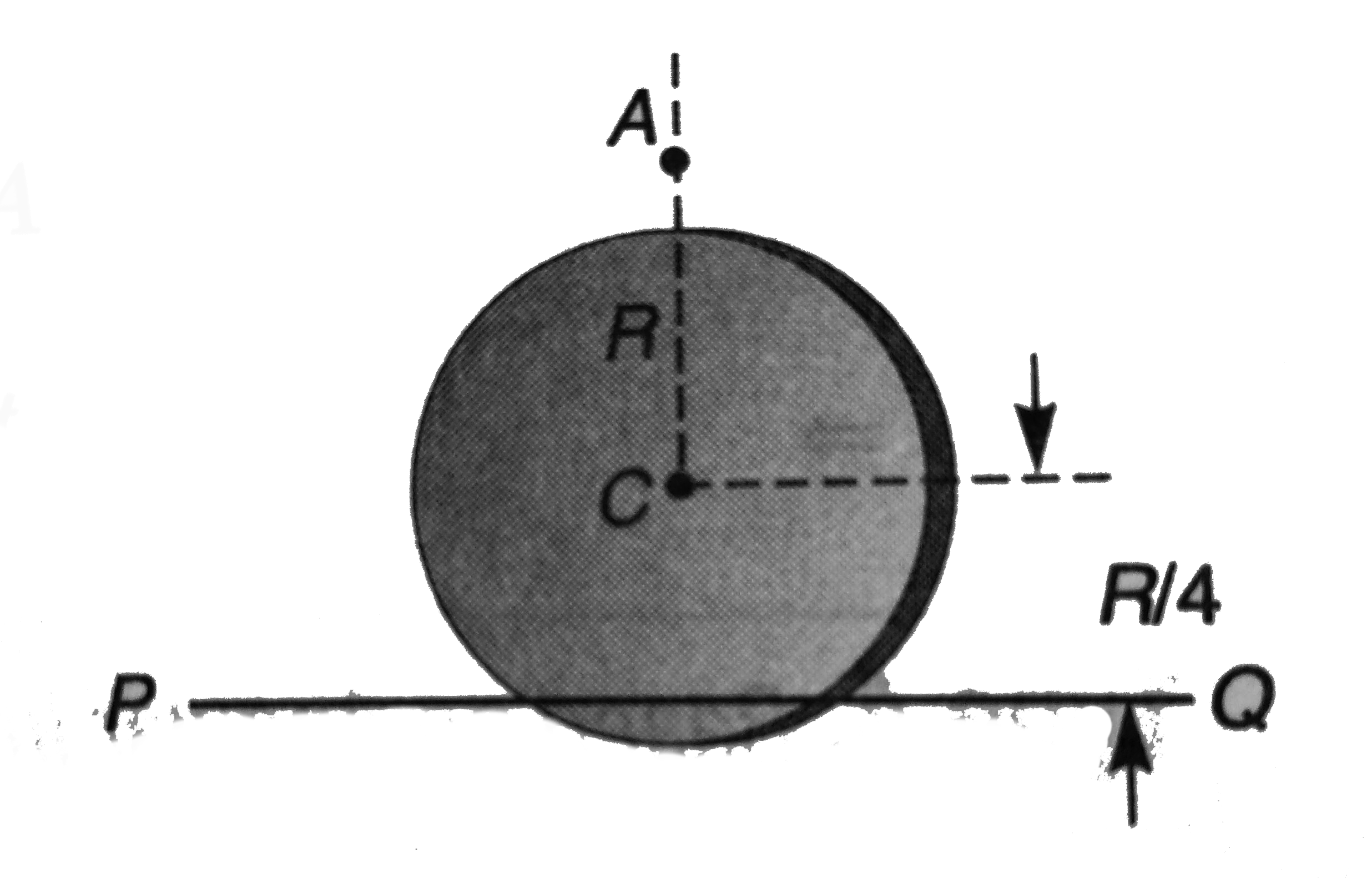
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.
View SolutionWater drops are falling from a tap at regular time intervals. When the fifth drop is near to fall from tap the first drop is at ground. If the tap is fixed at height H from ground then find out
(i) the height of the second drop from ground
(ii) distance between the second and third drop
(iii) velocity of third drop
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
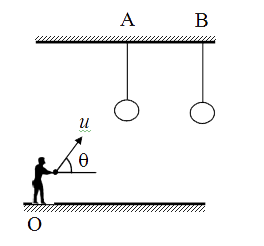
The maximum height attained by the ball above the floor is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
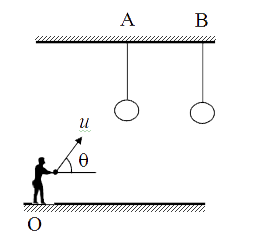
The projection speed of the ball is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.

When the ball lands on the floor, the stop watch reads:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
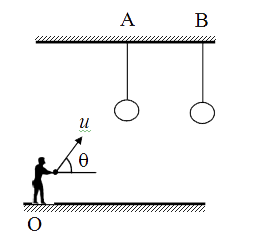
The ball lands on the floor at a distance:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.

The projection speed of the ball is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
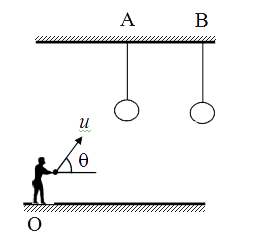
The angle of projection of the ball is:
View Solution
