An ideal monoatomic gas is initially in state with pressure and volume . If is then taken to state with pressure and volume . The change in internal energy from state to state is equal to
The correct Answer is:D
To solve the problem of finding the change in internal energy from state 1 to state 2 for an ideal monoatomic gas, we can follow these steps:
Step 1: Understand the Internal Energy Formula
The change in internal energy (ΔU) for an ideal gas is given by the formula:
ΔU=NCvΔT
where:
- N is the number of moles of the gas,
- Cv is the molar heat capacity at constant volume,
- ΔT is the change in temperature.
For a monoatomic ideal gas, the value of Cv is:
Cv=32R
where R is the universal gas constant.
Step 2: Use the Ideal Gas Law
The ideal gas law states:
PV=nRT
From this equation, we can derive the change in internal energy in terms of pressure and volume.
Step 3: Express ΔU in terms of P and V
We can express the change in internal energy as:
ΔU=32NRΔT=32NR(Δ(PV)R)=32Δ(PV)
Thus, we can write:
ΔU=32(PfVf−PiVi)
where:
- Pf and Vf are the final pressure and volume,
- Pi and Vi are the initial pressure and volume.
Step 4: Substitute the Given Values
From the problem:
- P1=20atm
- V1=1500cm3
- P2=1.5P1=1.5×20=30atm
- V2=2V1=2×1500=3000cm3
Now, substituting these values into the equation for ΔU:
ΔU=32(P2V2−P1V1)
=32(30atm×3000cm3−20atm×1500cm3)
Step 5: Calculate the Values
Convert the units:
- 1atm=105N/m2
- 1cm3=10−6m3
Thus, we convert:
- P1=20×105N/m2
- P2=30×105N/m2
- V1=1500×10−6m3
- V2=3000×10−6m3
Now substituting these into the ΔU equation:
ΔU=32((30×105)(3000×10−6)−(20×105)(1500×10−6))
=32(30×3−20×1.5)×105×10−6
=32(90−30)×10−1
=32×60×10−1
=90×10−1=9000J
Final Answer
The change in internal energy from state 1 to state 2 is:
ΔU=9000J
The change in internal energy (ΔU) for an ideal gas is given by the formula:
ΔU=NCvΔT
where:
- N is the number of moles of the gas,
- Cv is the molar heat capacity at constant volume,
- ΔT is the change in temperature.
Cv=32R
where R is the universal gas constant.
The ideal gas law states:
PV=nRT
From this equation, we can derive the change in internal energy in terms of pressure and volume.
We can express the change in internal energy as:
ΔU=32NRΔT=32NR(Δ(PV)R)=32Δ(PV)
Thus, we can write:
ΔU=32(PfVf−PiVi)
where:
- Pf and Vf are the final pressure and volume,
- Pi and Vi are the initial pressure and volume.
From the problem:
- P1=20atm
- V1=1500cm3
- P2=1.5P1=1.5×20=30atm
- V2=2V1=2×1500=3000cm3
ΔU=32(P2V2−P1V1)
=32(30atm×3000cm3−20atm×1500cm3)
Convert the units:
- 1atm=105N/m2
- 1cm3=10−6m3
- P1=20×105N/m2
- P2=30×105N/m2
- V1=1500×10−6m3
- V2=3000×10−6m3
ΔU=32((30×105)(3000×10−6)−(20×105)(1500×10−6))
=32(30×3−20×1.5)×105×10−6
=32(90−30)×10−1
=32×60×10−1
=90×10−1=9000J
The change in internal energy from state 1 to state 2 is:
ΔU=9000J
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -III
25 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -IV
9 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCE ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
64 Videos
Similar Questions
An ideal monoatomic gas initially in state 1 with pressure P1=20 atm and volume V11500cm3 it is then taken to state 2 with pressure P2=1.5P1 and volume V2=2V1 find the change in internal energy in this process in KJ. (take 1atm lit =100J)
View SolutionA monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionTwo moles of an ideal monoatomic gas, initially at pressure p1 and volume V1, undergo an adiabatic compression until its volume is V2. Then the gas is given heat Q at constant volume V2.
(i) Sketch the complete process on a p-V diagram.
(ii) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of p1,V1,V2,QandR]
View SolutionAn ideal gas (Cp/Cv=γ) having initial pressure P0 and volume V0 (a) The gas is taken isothermally to a pressure 2P0 and then adiabatically to a pressure 4P0. Find the final volume. (b) The gas is brought back to its initial state. It is adiabatically taken to a pressure 2P0 and then isothermally to a pressure 4P0. Find the final volume.
View SolutionAn ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature T1, pressure P1 and volume V1and the spring is in its relaxed state. The gas is then heated very slowly to temperature T2,pressure P2and volume V2. During this process the piston moves out by a distance x. Ignoring the friction between the piston and the cylinder, the correct statement (s) is (are)

View SolutionConsider a P−V diagram in which the path followed by one mole of perfect gas in a cyclinderical container is shown in (figure)
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures T1/T2,ifV2=2V1?
(c ) Given the internal energy for one mole of gas at temperature Tis(3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2=2V1.
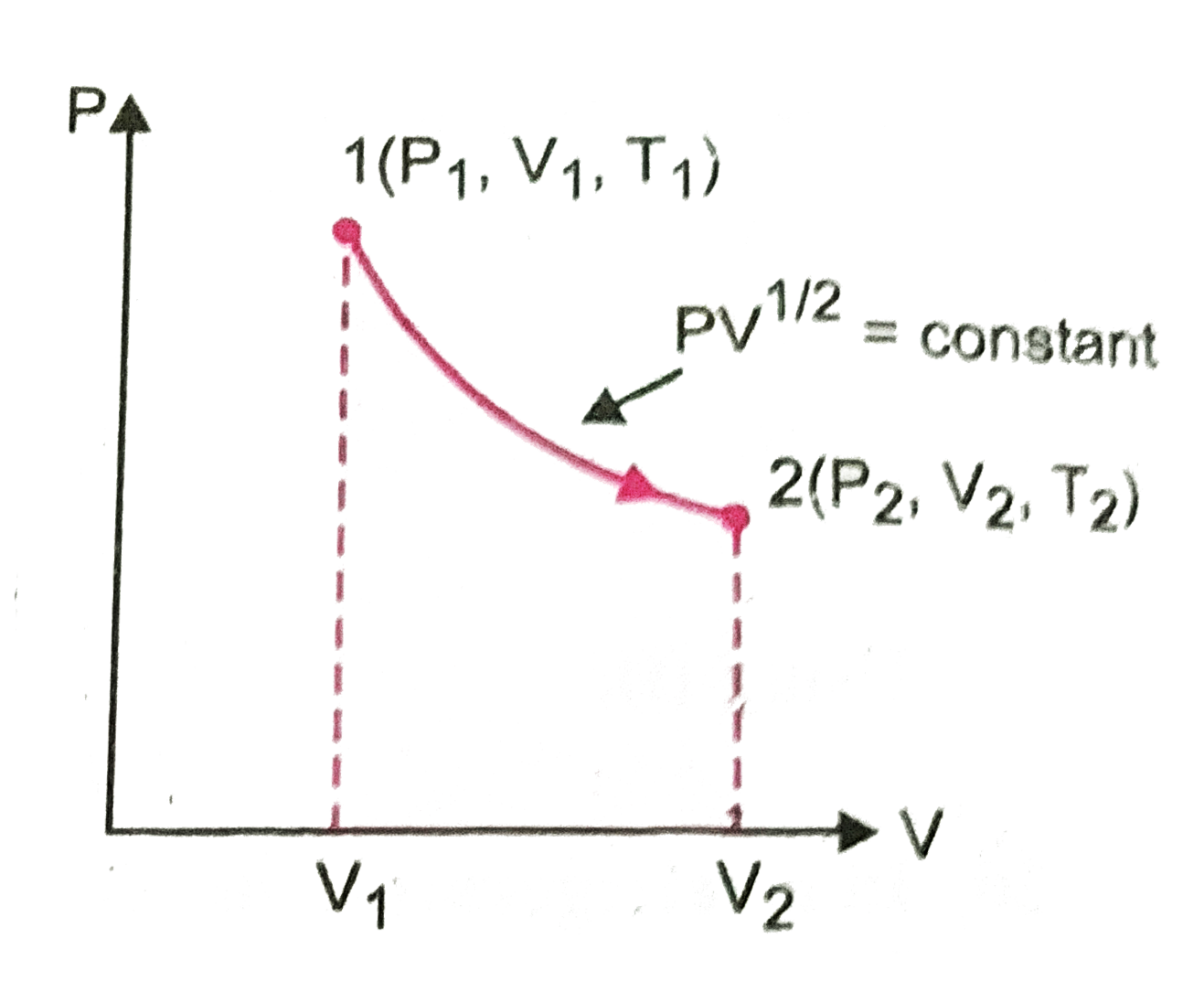
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
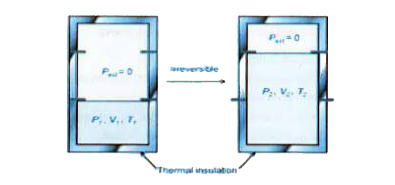
View SolutionAn ideal gas (CpCv=γ)has initial volume V0 is kept in a vessel. It undergoes a change and follows the following relation P=kV2 (where P is pressure, and V is volume) find the change in internal energy of the gas if its final pressure is P0:
View SolutionUnit mass of liquid of volume V1 completely turns into a gas of volume V2 at constant atmospheric pressure P and temperature T. The latent heat of vaporization is "L". Then the change in internal energy of the gas is
View Solution
