A mono-atomic ideal gas is compressed form volume V to V/2 through various process. For which of the following processes final pressure will be maximum:
isobaric
isothermal
adiabatic
PV2= constant
The correct Answer is:D
To determine which process results in the maximum final pressure when a monoatomic ideal gas is compressed from volume V to V2, we will analyze four different processes: isobaric, isothermal, adiabatic, and a process where PV2 is constant.
1. Identify Initial Conditions:
- Let the initial pressure be Pi=P0.
- The initial volume is Vi=V.
- The final volume is Vf=V2.
2. Isobaric Process:
- In an isobaric process, the pressure remains constant.
- Therefore, the final pressure Pf is:
Pf=Pi=P0
3. Isothermal Process:
- In an isothermal process, the temperature remains constant.
- Using the ideal gas law PV=nRT, we have:
PiVi=PfVf
- Substituting the values:
P0V=Pf(V2)
- Rearranging gives:
Pf=2P0
4. Adiabatic Process:
- For an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
- For a monoatomic gas, γ=53.
- Thus, we have:
PiVγi=PfVγf
- Substituting the values:
P0V53=Pf(V2)53
- Rearranging gives:
Pf=P0⎛⎝VV2⎞⎠53=P0(2)53=P0⋅253
5. Process where PV2 is Constant:
- For this process, we have:
PiV2i=PfV2f
- Substituting the values:
P0V2=Pf(V2)2
- Rearranging gives:
Pf=P0⋅4
6. Comparison of Final Pressures:
- From the calculations:
- Isobaric: Pf=P0
- Isothermal: Pf=2P0
- Adiabatic: Pf=P0⋅253≈2.519P0
- PV2 constant: Pf=4P0
- Comparing these values:
- P0<2P0<2.519P0<4P0
7. Conclusion:
- The maximum final pressure occurs in the process where PV2 is constant, yielding Pf=4P0.
Final Answer:
The final pressure will be maximum for the process where PV2 is constant.
- Let the initial pressure be Pi=P0.
- The initial volume is Vi=V.
- The final volume is Vf=V2.
- In an isobaric process, the pressure remains constant.
- Therefore, the final pressure Pf is:
Pf=Pi=P0
- In an isothermal process, the temperature remains constant.
- Using the ideal gas law PV=nRT, we have:
PiVi=PfVf
- Substituting the values:
P0V=Pf(V2)
- Rearranging gives:
Pf=2P0
- For an adiabatic process, the relationship between pressure and volume is given by:
PVγ=constant
- For a monoatomic gas, γ=53.
- Thus, we have:
PiVγi=PfVγf
- Substituting the values:
P0V53=Pf(V2)53
- Rearranging gives:
Pf=P0⎛⎝VV2⎞⎠53=P0(2)53=P0⋅253
- For this process, we have:
PiV2i=PfV2f
- Substituting the values:
P0V2=Pf(V2)2
- Rearranging gives:
Pf=P0⋅4
- From the calculations:
- Isobaric: Pf=P0
- Isothermal: Pf=2P0
- Adiabatic: Pf=P0⋅253≈2.519P0
- PV2 constant: Pf=4P0
- P0<2P0<2.519P0<4P0
- The maximum final pressure occurs in the process where PV2 is constant, yielding Pf=4P0.
The final pressure will be maximum for the process where PV2 is constant.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -III
Explore 25 Videos
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:PART -IV
Explore 9 Videos
- KTG & THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KTG & THERMODYNAMICSExercise:Exercise-2
Explore 1 Video
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCE ENGLISHChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCE ENGLISHChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 64 Videos
Similar Questions
An ideal gas is compressed to half its initial volume by means of several peocesses. Which of the process results in the maximum work done on the gas ?
View SolutionStatement I: A gas is expanded from a volume V to 2V, first through adiabatic process then through isothermal process. Work done in isothermal process is more if final state (i.e. pressure and volume ) in both the cases is same.
Statement II: Work done by the gas is equal to area under p−V curve.

View Solution
Knowledge Check
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
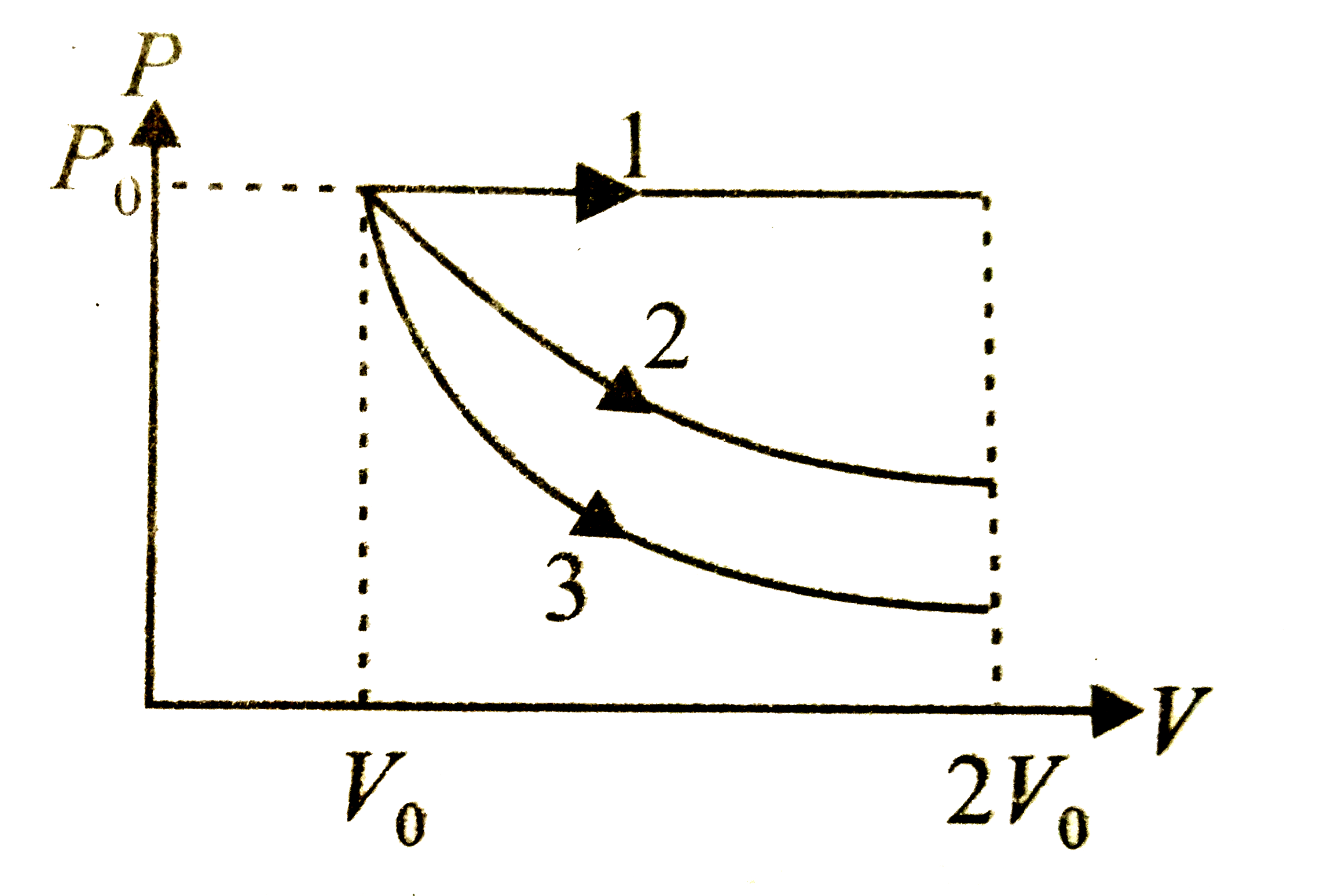 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3Two samples, A and B of a gas at the same initial temperature and pressure are compressed from volume V to V/2, A isothermally and B adiabatically. The final pressure of A will be
Agreater than that of BBequal to that of BCless than of BDtwice that of B
The pressure v/s volume graph of an ideal gas is given different thermodynamics process which of the following option relevant in order : (Isochoric, isobaric, isothermal, adiabatic)
_2019_CBT2_E01_013_Q01.png)
View SolutionA monoatomic gas at pressure P1 and volume V1 is compressed adiabatically to 18th of its original volume. What is the final pressure of gas.
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be

View SolutionA sample of an ideal gas with initial pressure 'P' and volume 'V' is taken through an isothermal process during which entropy change is found to be DS. The work done by the gas is
View SolutionA mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate
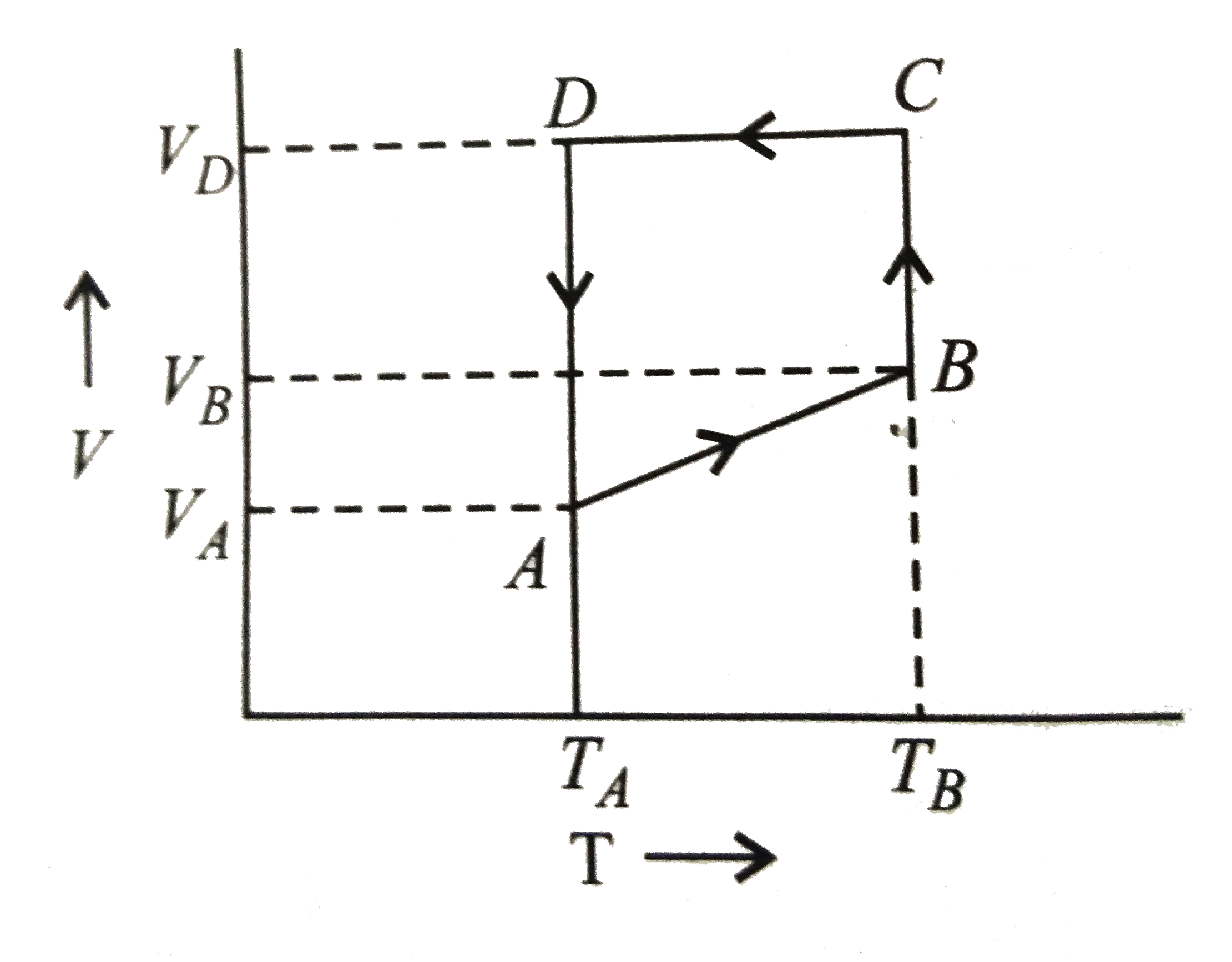
a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total work done in cyclic process.
View SolutionA mono-atomic ideal gas of two moles is taken through a cyclic process starting from A as shwon in the figure below.
The volume ratios are VB/VA=2 and VD/VA=4. If the temperature TA at A is 27∘C. Calculate

a. The temperature of gas at B.
b. Heat absorbed or evolved in each process.
c. Total wrok done in cyclic process.
View Solution

