Question

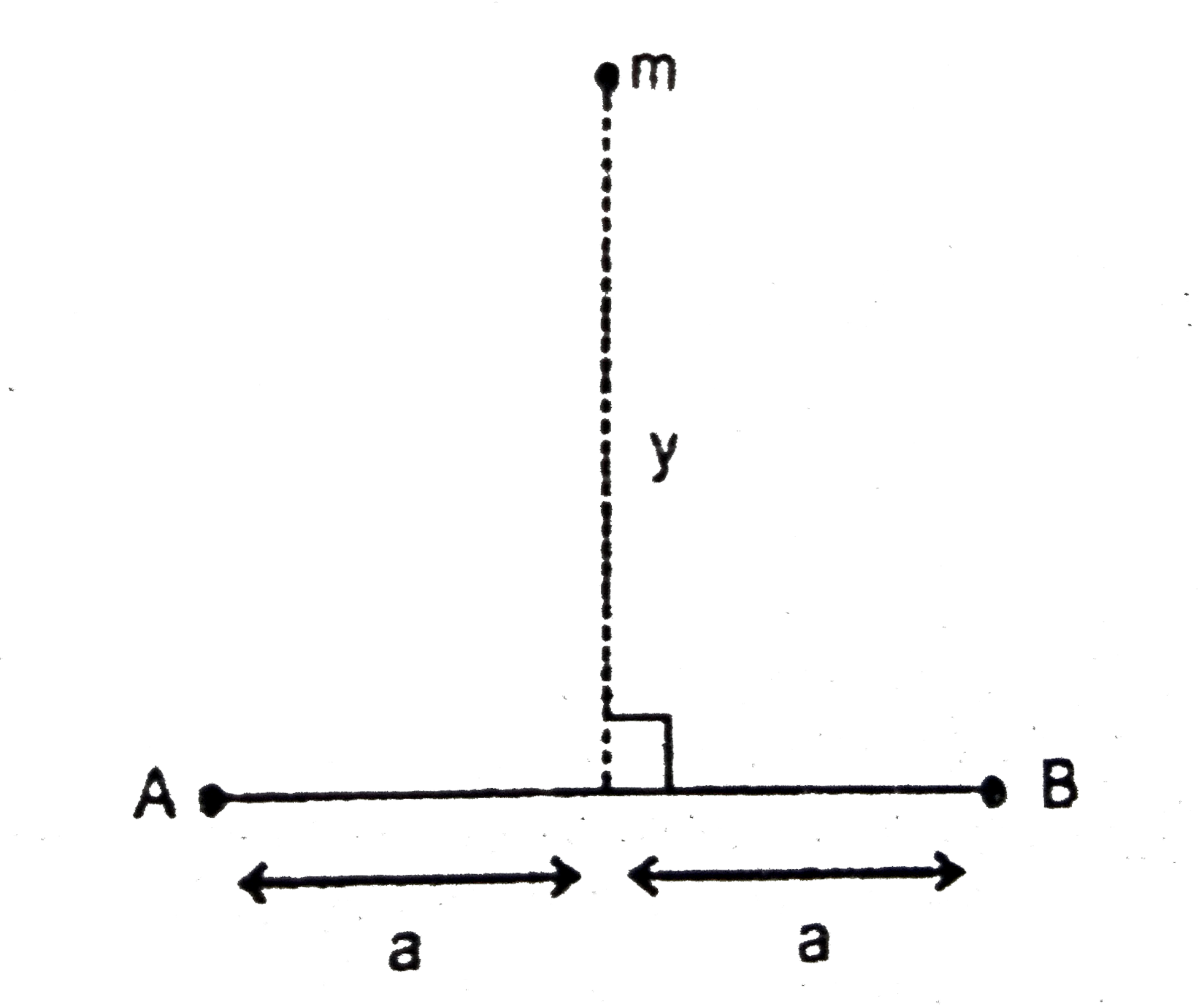
Potential energy of a particle of mass $m$, depends on distance $y$ from line $AB$ according to given relation $U=\frac{K}{\sqrt{y^2+a^2}}$, where $K$ is a positive constant. A particle of mass $m$ is projected from $y=\sqrt{3}$ towards line $AB$. (perpendicular to it) then minimum velocity so that it connot return to its initial point is $\sqrt{\frac{K}{aNm}}$, calculate $N$.

Answer

1

Explanation

`U_(i) + k_(i) = U_(f) + k_(f)`
`(K)/(2a) + (1)/(2)mV_(0)^(2) = (K)/(a)`
`(mV_(0)^(2))/(2) = (K)/(2a) rArr v_(0) = sqrt((K)/(am))`