A light rod of length L is hanging from the vertical smooth wall of a vehicle moving with acceleration √3g along the horizontal plane having a small mass attached at its one end is free to rotate about an axis passing through the other end. The minimum velocity given to the mass at its equilibrium position with respect to the vehicle so that it can complete vertical circular motion is
The correct Answer is:8
geff=√g2+a2=√g2+3g2=2g
Vmin at equilibrium position =√4geffl
=√4(2g)l
=√8gl
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A light rod length L, is hanging from the vertical smooth wall of a vehicle moving with acceleration √3g having a small mass attached at its one end is free to rotate about an axis passing through the other end. The minimum velocity given to the mass at its equilibrium position with respect to vehicle so that it can complete vertical circular motion respect to vehical) is √KgL. Find the value of K.
View SolutionFind the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).

View SolutionA particle of mass of mass m is attached to a light rod of lenght l other end of the rod is hinged to a wall . Minimumm velocity (Vo) that should be given to a particle in lowest positiion so that it completes a vertical circle
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
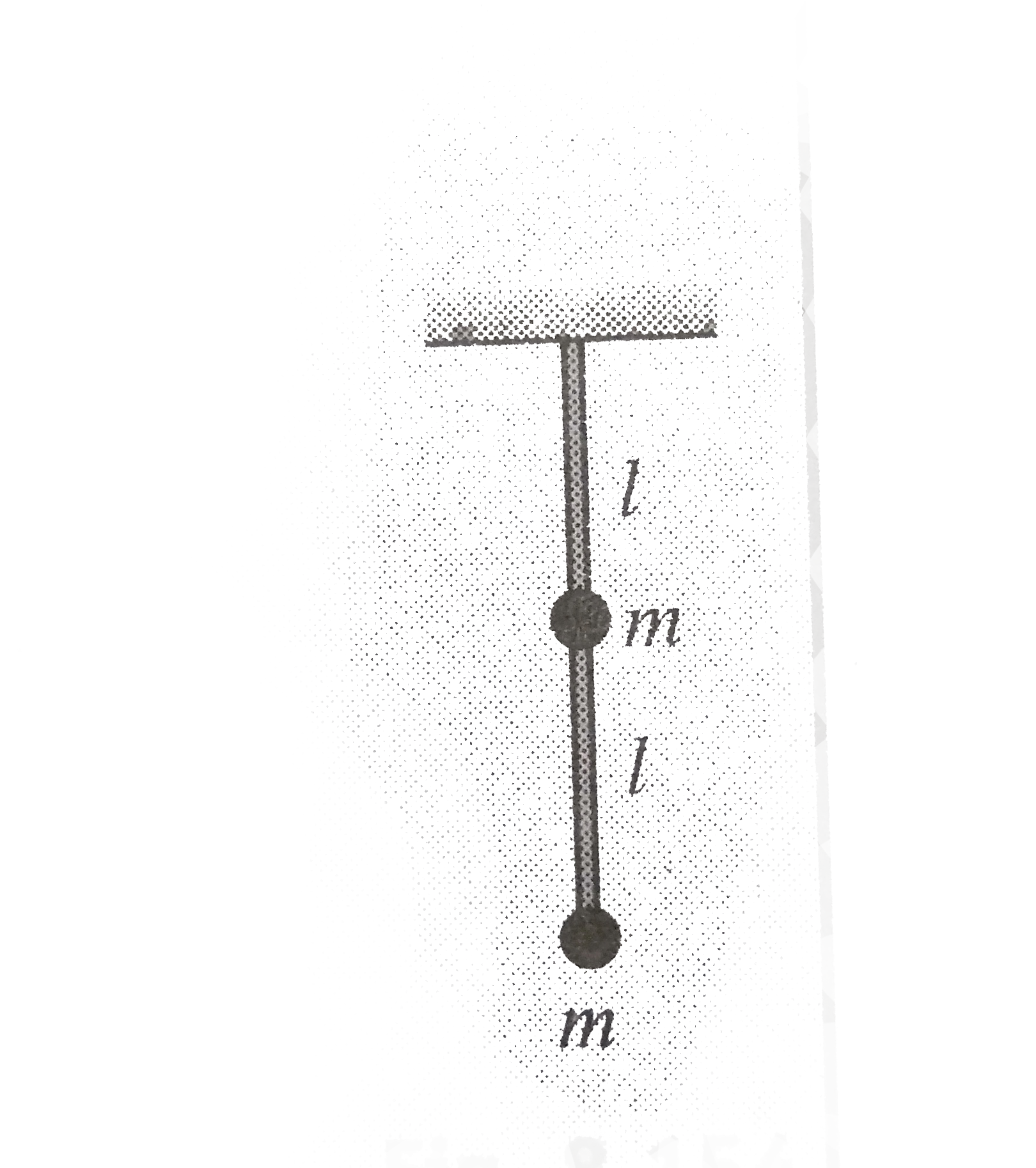
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
View Solution

