A skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from top of a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is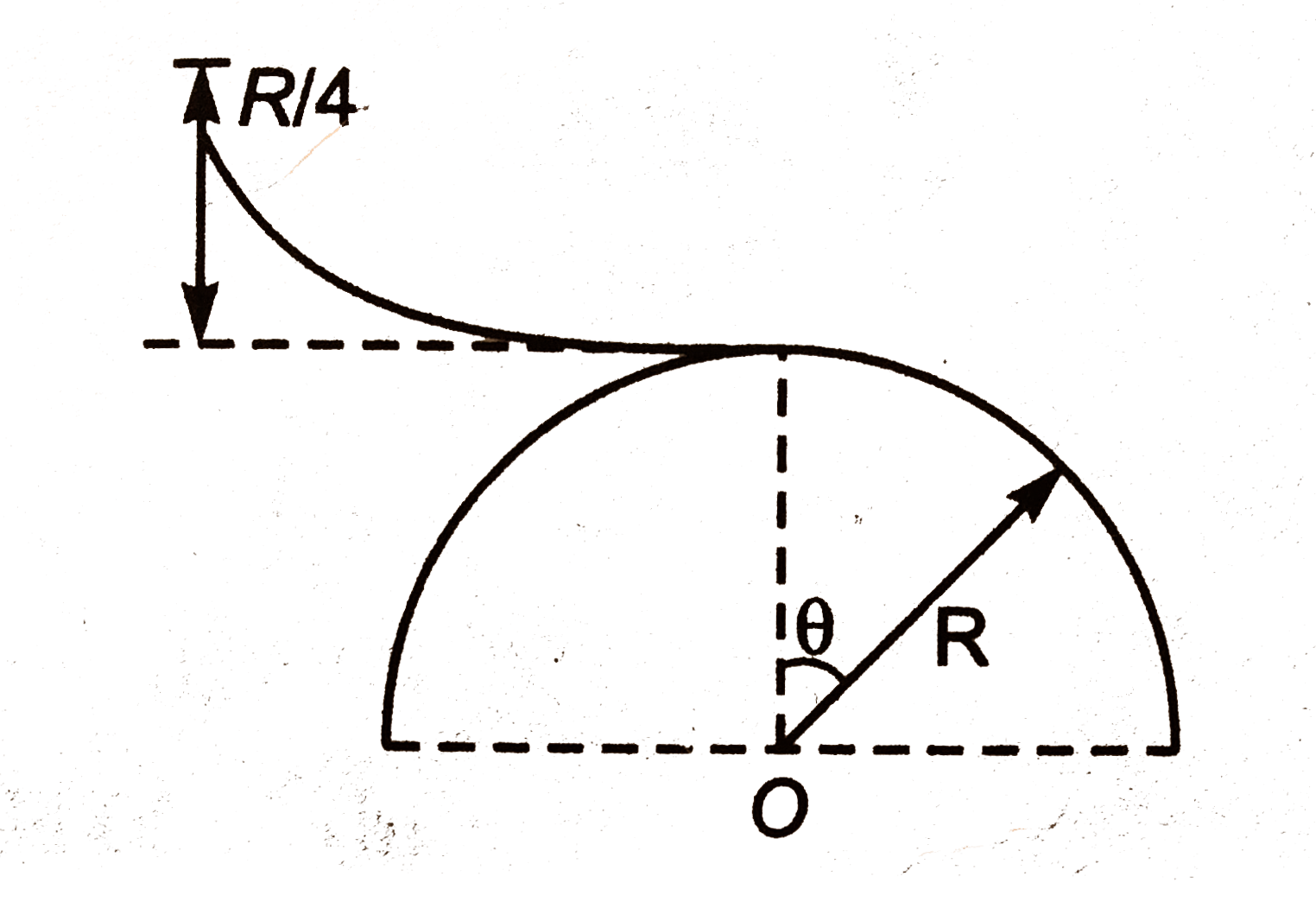 
cos−1(2/3)
cos−1(5/√3)
cos−1(5/6)
cos−1(5/2√3)
The correct Answer is:C
A skier plans …………..
Δh=R4+R(1−cosθ)
12mv2=mgΔh=mgR4{1+4(1−cosθ)}
∴mv2R=mg2(5−4cosθ)
mgcosθ−N=mv2R
mgcosθ=mg2(5−4cosθ)
cosθ=5/6
Topper's Solved these Questions
Similar Questions
A skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is
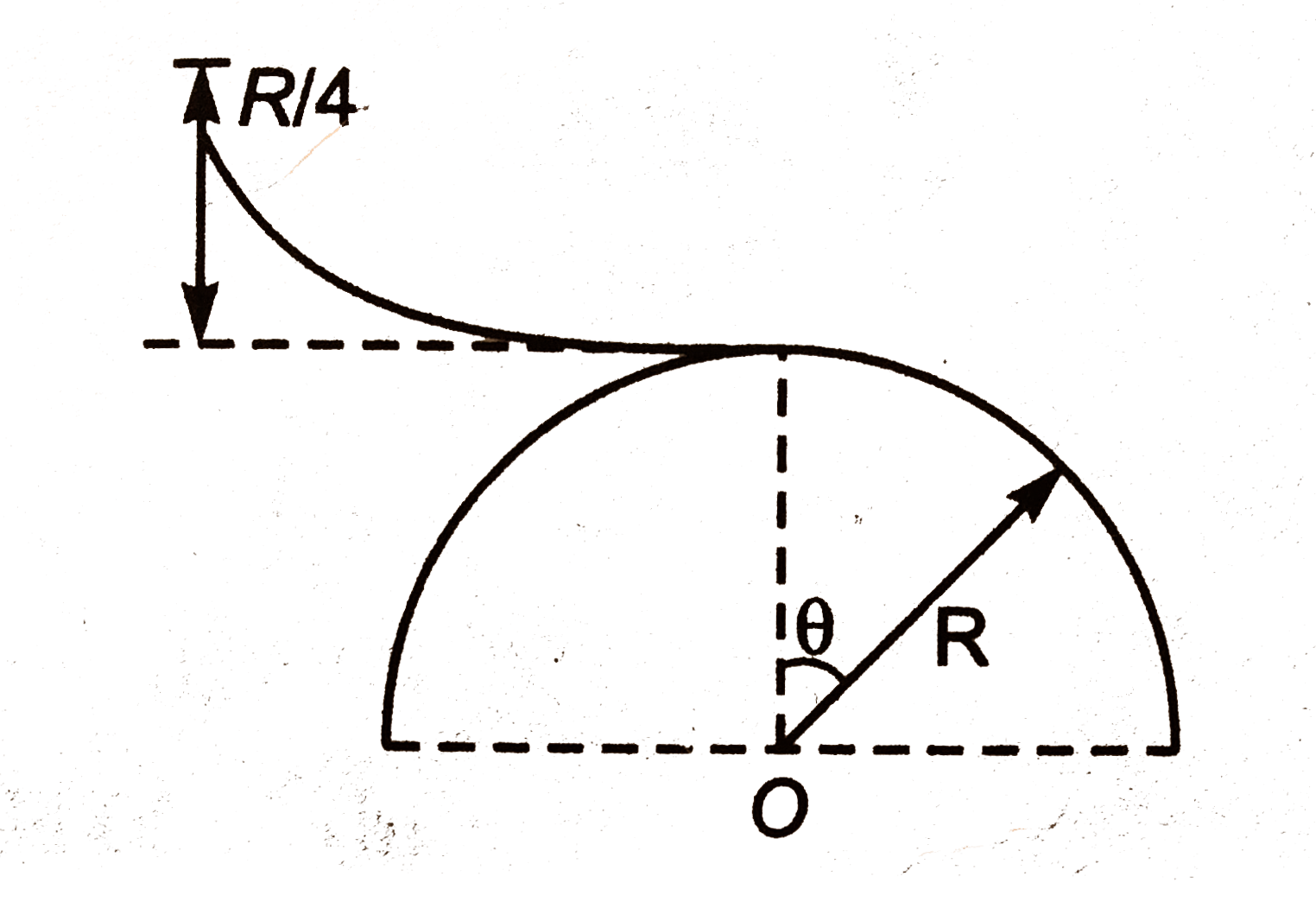
View SolutionA particle of mass m is placed in equilibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical where cosθ=35. if the work done against friction is 2mgR10x, find x.
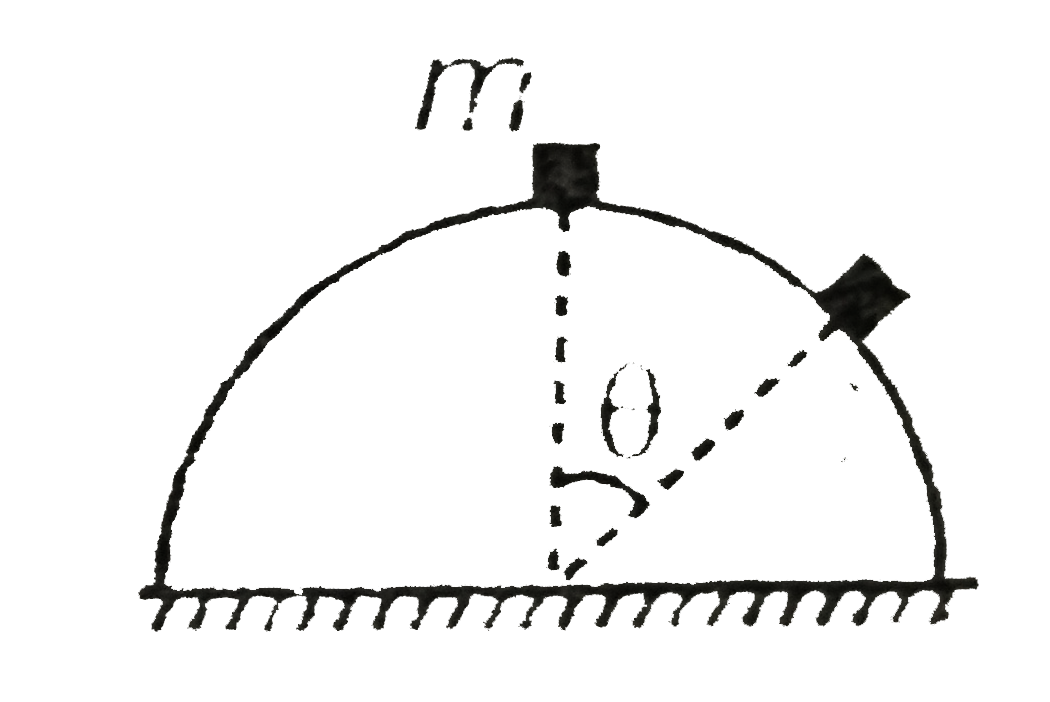
View Solution
Knowledge Check
- Question 1 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1 - Question 2 - Select One
A particle rests on the top of a hemishpere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is yo leave the hemisphere without sliding down it.
A√gRB√2gRC√3gRD√5gR
A small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
For u=u0/3, Find the height from the ground at which it leaves the hemisphereView SolutionA small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
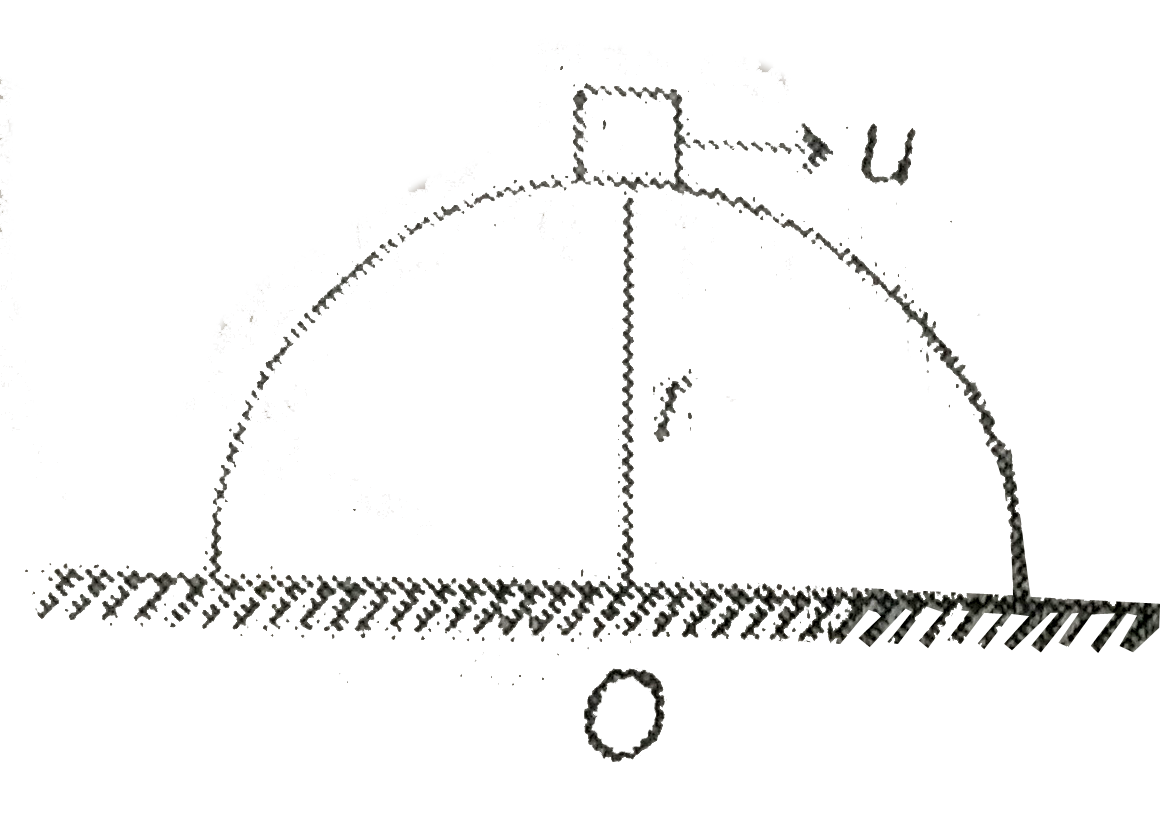
In the above problem find its net acceleration at the instant it levels the hemisphere.View SolutionA small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
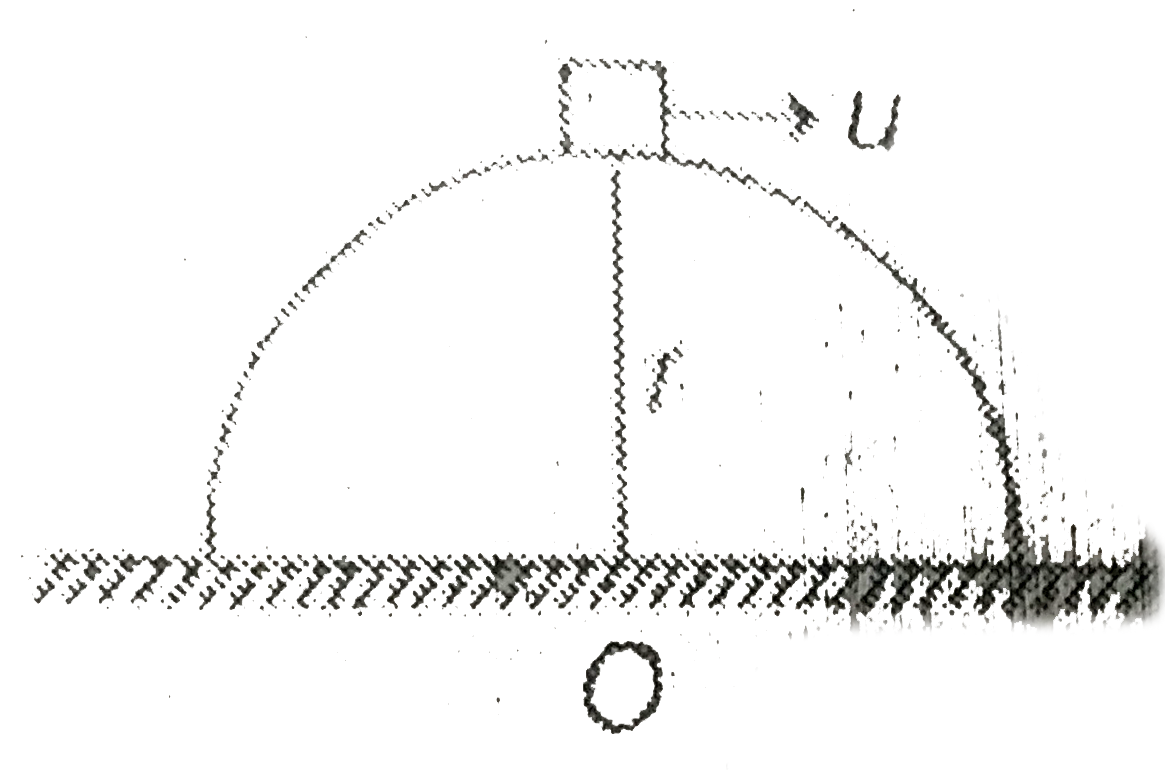
For u=2u0, it lands at point P on ground. Find OP.View SolutionA particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionA particle rests on the top of a smooth hemisphere of radius r. It is imparted a horizontal velocity of √ηgr. Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.
View SolutionA block of mass m moving on a fixed smooth hemisphere of rudius R. If speed of block at top most point of the hemisohere is √gR as shown in the figure, then the angle (θ) with the vertical, where the normal contact force becomes zero will be
View Solution