
A solid spherical planet of mass 2m and radius 'R' has a very small tunnel along its diameter. A small cosmic
particle of mass m is at a distance 2R from the centre of the planet as shown. Both are initially at rest, and due
to gravitational attraction, both start moving toward each other. After some time, the cosmic particle passes
through the centre of the planet. (Assume the planet and the cosmic particle are isolated from other planets)
4R3
velocity of the cosmic particle at that instant is
√8Gm3R
Total work done by the gravitational force on both the particle is −2Gm2R
Total work done by the gravitational force on both the particle is −2Gm2R
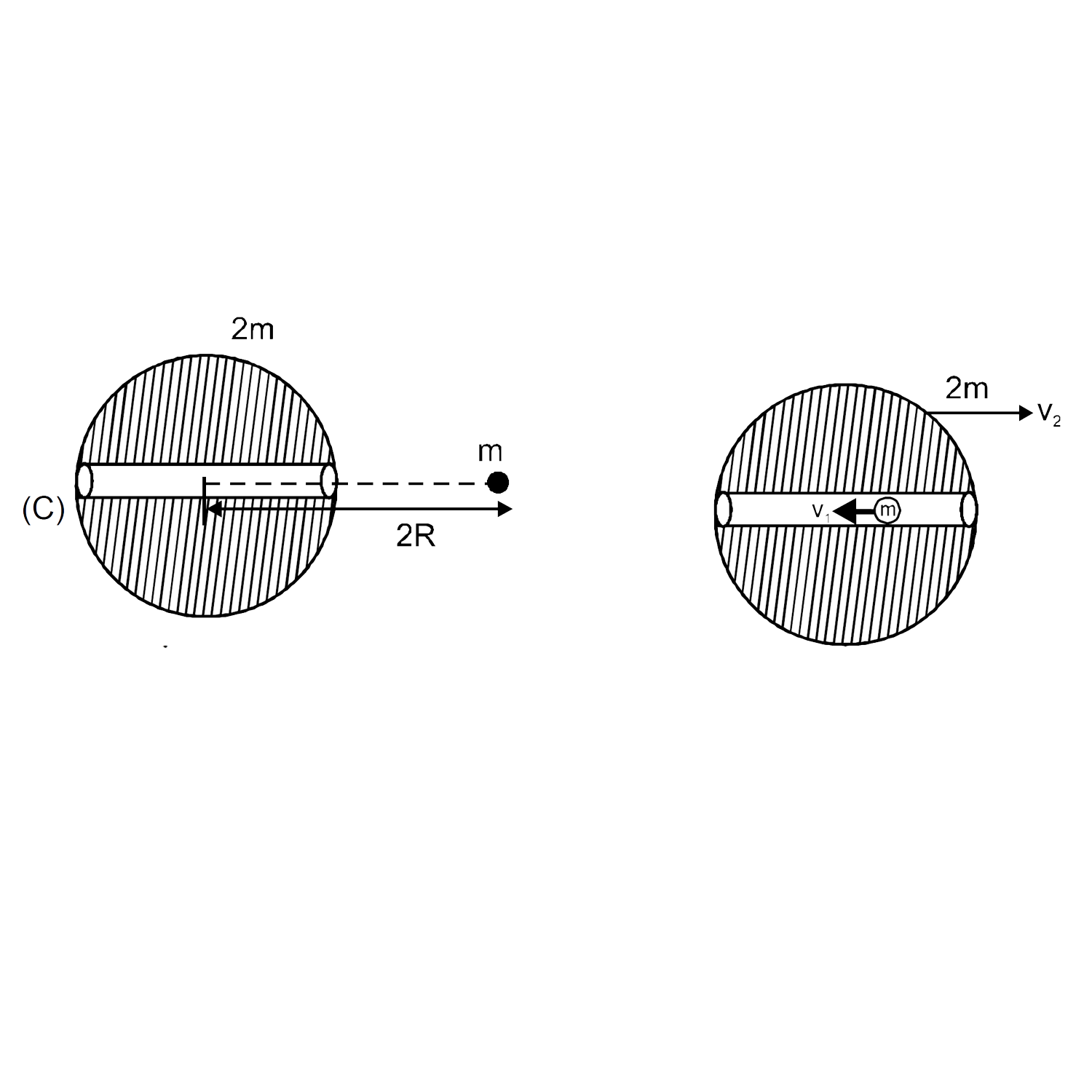
Applying momentum conservation
0=mv1−2mv2
⇒v2=v12 ..(i) Ki+Ui=kf+Uf
0+(−G(2m)2R)m=12mv21+12(2m)v22+(−32G(2m)R)(m) ..(ii)
Solving eqs. (i) and (ii) get
(A) COM will be fixed so
Scm=m1s1+m2s2m1+m2
0=(m)(x)+(2m)(−(2R−x))m+2m⇒x=4R3
(B). Fnet=0⇒a=0
(D). Wgr=U⏐⏐
⏐
⏐
⏐↓⇒Wgr=(−G(2m)2R)m−(−32G(2m)R)m
Topper's Solved these Questions
Similar Questions
_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle for that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionThe escape velocity for a planet is ve. A particle starts from rest at a large distance from the planet, reaches the planet only under gravitational attraction, and passes through a smooth tunnel through its centre. Its speed at the centre of the planet will be
View Solution