A kite is attached to a string. Find the length of the string , when the height of the kite is 60 m and the string makes an angle 30∘ with the ground .
The correct Answer is:120 m
To find the length of the string attached to the kite, we can use trigonometric ratios. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a kite at a height of 60 meters, and the string makes an angle of 30 degrees with the ground. We need to find the length of the string.
Step 2: Draw a Diagram
Draw a right triangle where:
- Point A is the position of the kite.
- Point B is the point on the ground directly below the kite.
- Point C is the point where the string is attached to the ground.
In this triangle:
- AB (height of the kite) = 60 m
- Angle ABC = 30 degrees
- AC (length of the string) is what we need to find.
Step 3: Use Trigonometric Ratios
In a right triangle, we can use the sine function, which is defined as:
sin(θ)=OppositeHypotenuse
Here, the opposite side is AB (height of the kite) and the hypotenuse is AC (length of the string).
Step 4: Set Up the Equation
Using the sine function:
sin(30∘)=ABAC
Substituting the known values:
sin(30∘)=60AC
Step 5: Calculate the Value of Sine
We know that:
sin(30∘)=12
So, substituting this into the equation gives:
12=60AC
Step 6: Solve for AC
Cross-multiplying to solve for AC:
AC⋅12=60
AC=60⋅2
AC=120 m
Conclusion
The length of the string is 120 meters.
---
We have a kite at a height of 60 meters, and the string makes an angle of 30 degrees with the ground. We need to find the length of the string.
Draw a right triangle where:
- Point A is the position of the kite.
- Point B is the point on the ground directly below the kite.
- Point C is the point where the string is attached to the ground.
- AB (height of the kite) = 60 m
- Angle ABC = 30 degrees
- AC (length of the string) is what we need to find.
In a right triangle, we can use the sine function, which is defined as:
sin(θ)=OppositeHypotenuse
Here, the opposite side is AB (height of the kite) and the hypotenuse is AC (length of the string).
Using the sine function:
sin(30∘)=ABAC
Substituting the known values:
sin(30∘)=60AC
We know that:
sin(30∘)=12
So, substituting this into the equation gives:
12=60AC
Cross-multiplying to solve for AC:
AC⋅12=60
AC=60⋅2
AC=120 m
The length of the string is 120 meters.
Topper's Solved these Questions
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 B
19 Videos
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 C
28 Videos
- HEIGHTS AND DISTANCES BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 C
28 Videos
- GST [GOODS AND SERVICES TAX] BOOK - ICSECHAPTER - GST [GOODS AND SERVICES TAX] EXERCISE - Exercise 1(B)
16 Videos
- LINEAR INEQUATIONSBOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions
15 Videos
Similar Questions
A kite is attached to a 100 m long string. Find the greatest height reached by the kite when its string makes an angle of 60∘ with the travel round.
View SolutionThe bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity √10gl where l is the length of the pendulum. Find the tension in the string when a. the string is horizontal. B. The bob is at its highest point and c. the string makes an angle of 600 with the upward vertical.
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
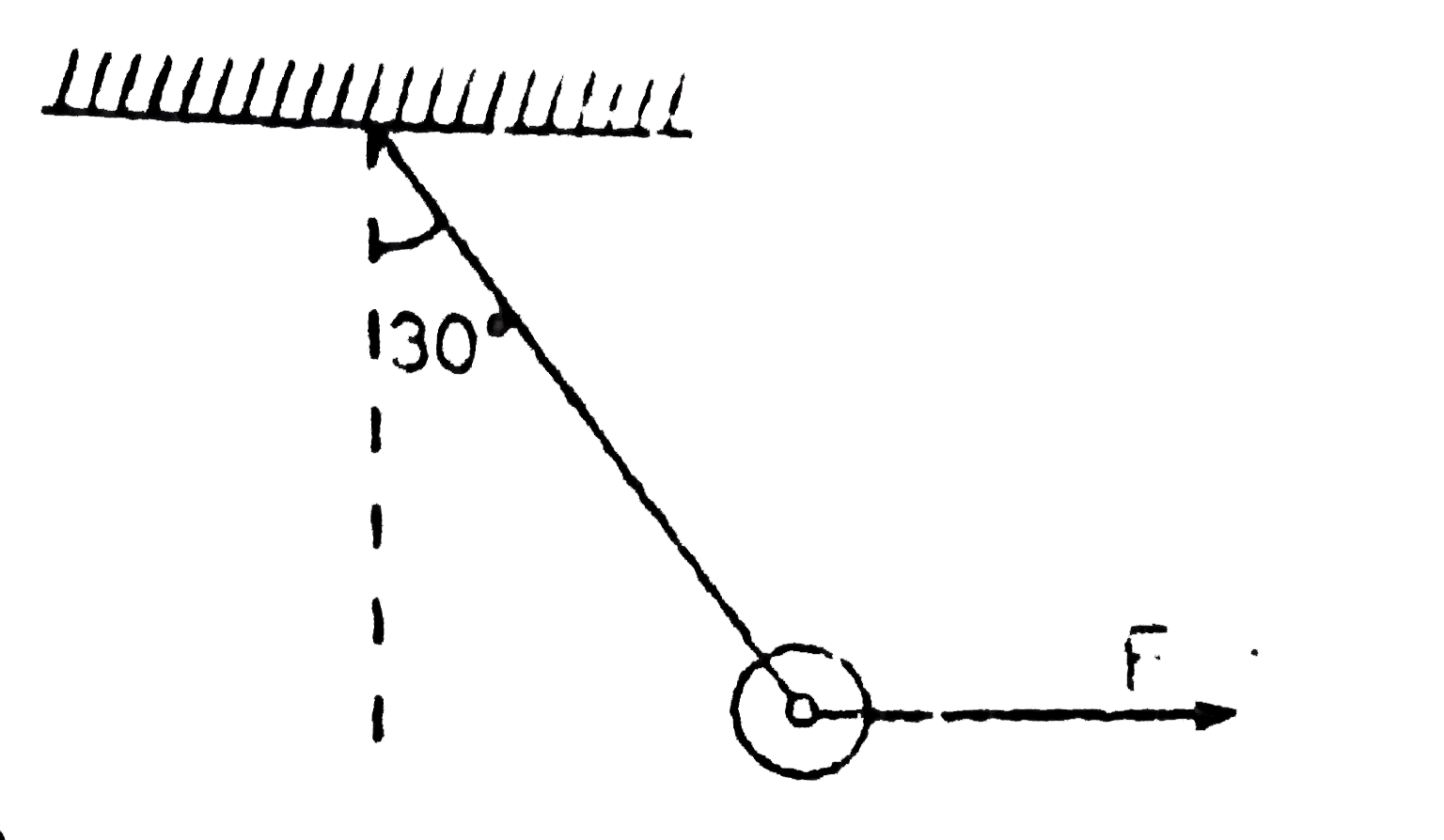 .
.
View SolutionA bead can slide on a smooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a distance.

View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA ring A which can slide on a smooth wire is connected to one end of a string as shown in fig. Other end of the string is connected to a hanging mass B. Find the speed of the ring when the string makes an angle θ with the wire and mass B is going down with a velocity v.
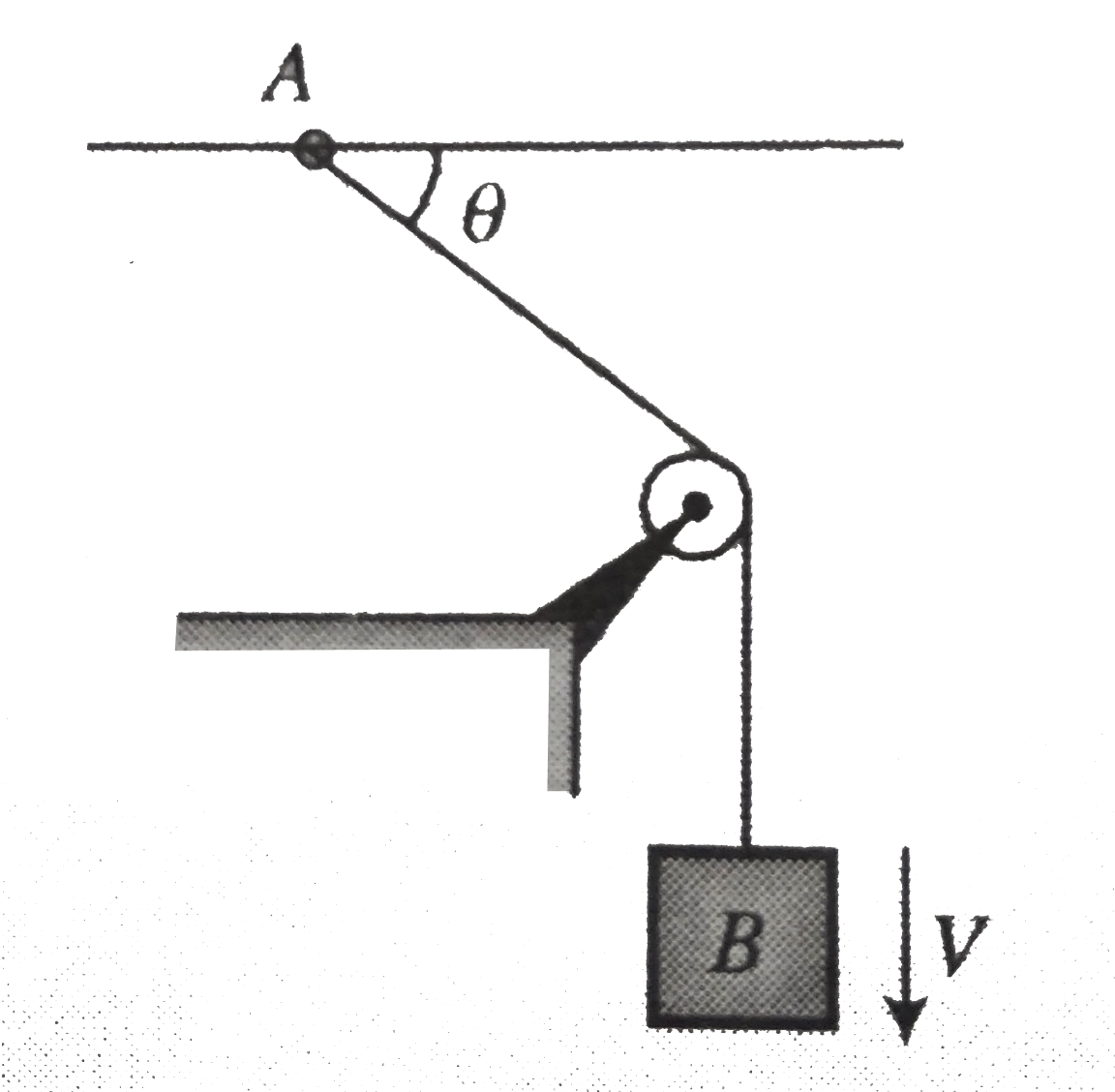
View SolutionA heavy particle is tied to the end A of a string of the length1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60∘ with the horizontal. Then,
View SolutionAn object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
View SolutionTwo small metallic spheres each of mass 'm' are suspended together with strings of length 'l' and placed together. When a quantum of charge 'q' is transferred to each the strings make and angle of 90∘ with each other. The value of 'q' is
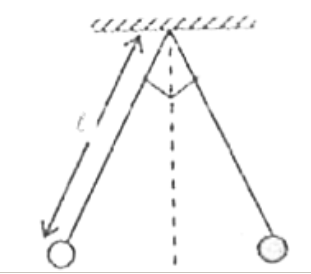
View SolutionWhen the string of a conical pendulum makes an angle of 45∘ with the vertical , its time is T1 when the string makes an angle of 60∘ with the vertical , its time period is T2 then T21/T22is
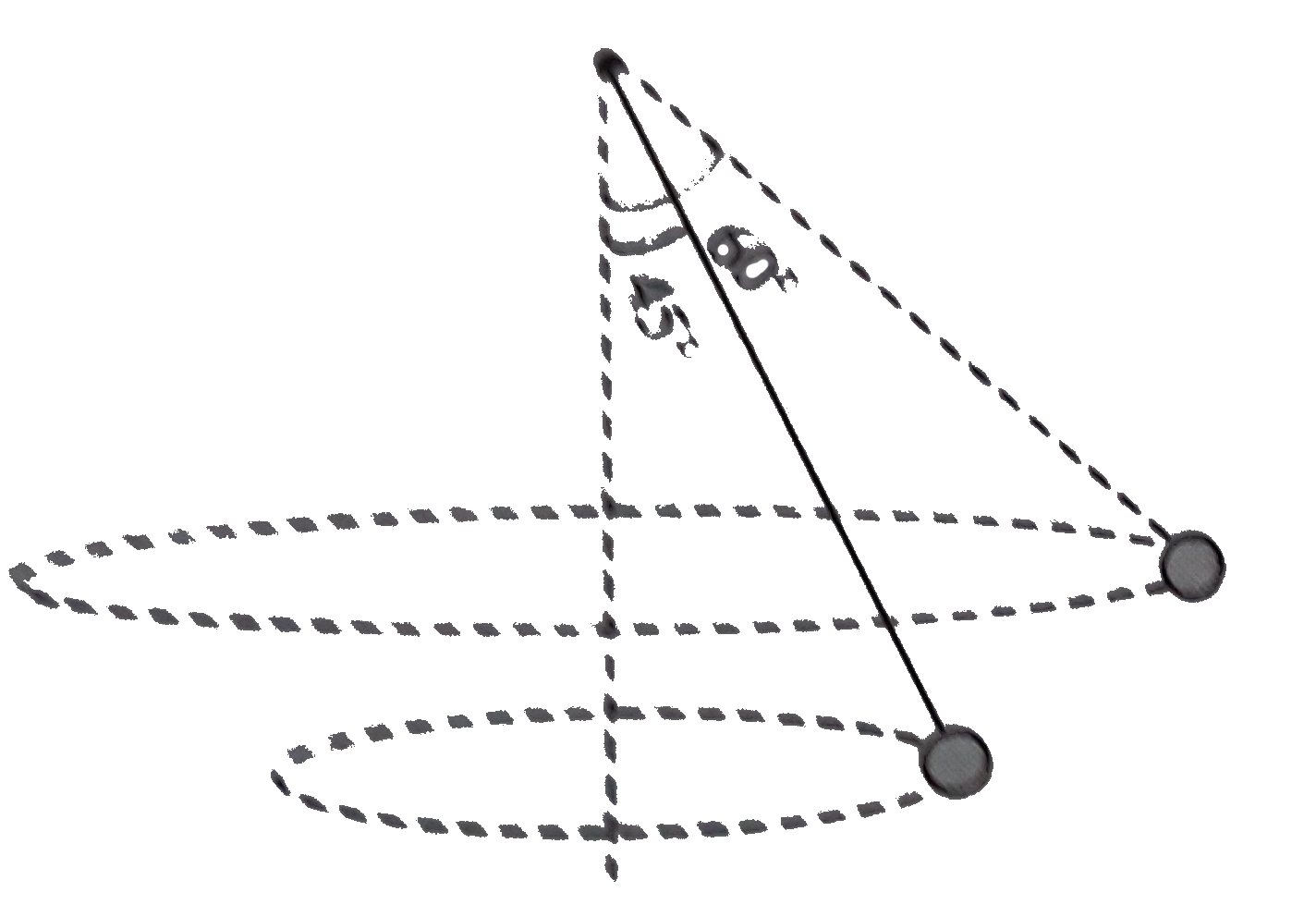
View Solution
