A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28∘ and the angle of depression of the bottom of the pole is 13∘ .Calculate the height of the pole .
The correct Answer is:6 . 86 m
Step by step video, text & image solution for A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28^(@) and the angle of depression of the bottom of the pole is 13^(@) .Calculate the height of the pole . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Related Playlists
- BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 B19videos
HEIGHTS AND DISTANCES
- BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 C28videos
HEIGHTS AND DISTANCES
- BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 C28videos
HEIGHTS AND DISTANCES
- BOOK - ICSECHAPTER - GST [GOODS AND SERVICES TAX] EXERCISE - Exercise 1(B)16videos
GST [GOODS AND SERVICES TAX]
- BOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions15videos
LINEAR INEQUATIONS
Similar Questions
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the pole, if the height of the tower is 75 mView SolutionA vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole the angle of elevation of the top of the tower is 60∘ and the angle of depression of the bottom of the tower is 30∘ . Find :
the height of the tower, it the height of the pole is 20 m ,View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA man standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a hill as 600 and the angle of depression of the base of the hill as 300. Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA man standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 60o and the angle of depression of the base of the hill as 30o . Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60∘ and the angle of depression the base of hill as 30∘. Find the distance of the hill from the ship and the height of the hill.
View SolutionA flag-staff stands on the top of a 5 m high tower. From a point on the ground, the angle of elevation of the top of the flag-staff is 60∘ and from the same point, the angle of elevation of the top of the tower is 45∘ . Find the height of the flag-staff.
View SolutionWith reference to the given figure, a man stands on the ground at point A, Which is on the same horizontal plane as B, the foot of the vertical pole BC. The height of the pole is 10 m . The man's eye is 2 m above the ground. He observes the angle of elevation of C, the top of the pole, as x∘ , where tan x∘=25 . Calculate :
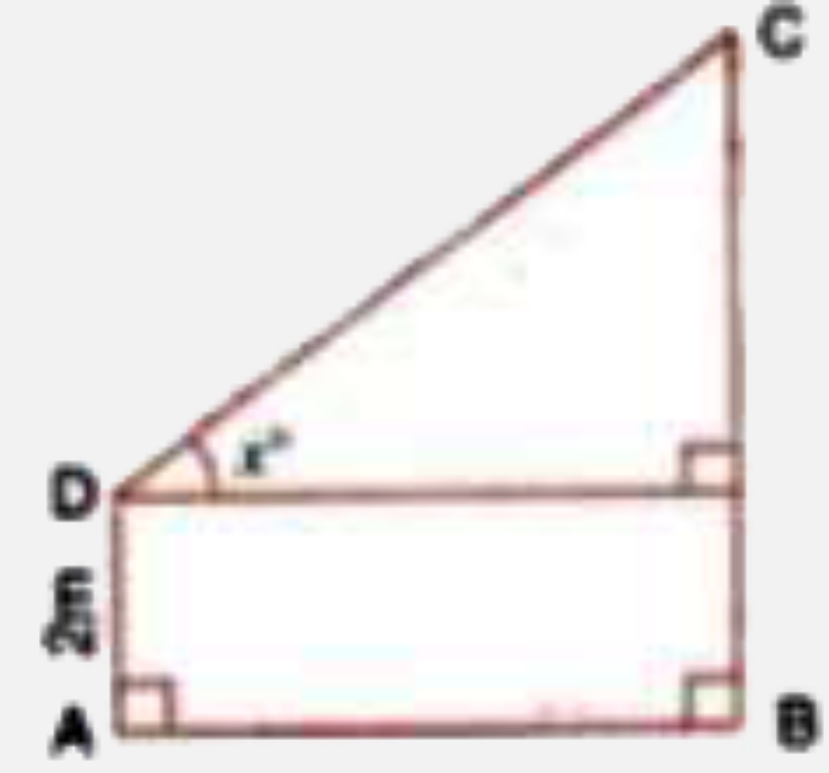
angle of elevation of the top of the pole when he is standing 15 metres from the pole. Give your answer to the nearest degree.View SolutionThe angle of elevation of the sun when the length of the shadow of a pole is √3 times the height of the pole is
View SolutionA 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60∘ and the angle of elevation of the top of the pole as seen from the foot of the tower is 30∘ . Find :
the horizontal distance between the pole and the tower.View Solution


