Three resistors each of 2 Ω are connected together so that their total resistance is 3 Ω. Draw a diagram to show this arrangement and check it by calculation.
To solve the problem of finding the total resistance of three resistors each of 2 Ω connected to achieve a total resistance of 3 Ω, we can follow these steps:
1. Understanding the Configuration:
- We need to connect three resistors (R1, R2, and R3) each of 2 Ω in such a way that the total resistance is 3 Ω.
- To achieve this, we can connect two resistors in parallel and then connect the third resistor in series with this combination.
2. Drawing the Diagram:
- Draw two resistors (R1 and R2) in parallel.
- Connect the third resistor (R3) in series with the parallel combination of R1 and R2.
R1∣|||||||⊢−−−−−−|R3||||||R2
3. Calculating the Equivalent Resistance of R1 and R2:
- The formula for the equivalent resistance (Ra) of two resistors in parallel is:
\(
\frac{1}{R_a} = \frac{1}{R_1} + \frac{1}{R_2}
\)
- Substituting the values:
\(
\frac{1}{R_a} = \frac{1}{2} + \frac{1}{2}
\)
- This simplifies to:
\(
\frac{1}{R_a} = \frac{2}{2} = 1 \implies R_a = 1 \, \Omega
\)
4. Calculating the Total Resistance:
- Now, we connect R3 (which is also 2 Ω) in series with the equivalent resistance Ra:
\(
R_{\text{total}} = R_a + R_3
\)
- Substituting the values:
\(
R_{\text{total}} = 1 \, \Omega + 2 \, \Omega = 3 \, \Omega
\)
5. Conclusion:
- The total resistance of the arrangement is indeed 3 Ω, as required.
- We need to connect three resistors (R1, R2, and R3) each of 2 Ω in such a way that the total resistance is 3 Ω.
- To achieve this, we can connect two resistors in parallel and then connect the third resistor in series with this combination.
- Draw two resistors (R1 and R2) in parallel.
- Connect the third resistor (R3) in series with the parallel combination of R1 and R2.
- The formula for the equivalent resistance (Ra) of two resistors in parallel is:
\(
\frac{1}{R_a} = \frac{1}{R_1} + \frac{1}{R_2}
\)
- Substituting the values:
\(
\frac{1}{R_a} = \frac{1}{2} + \frac{1}{2}
\)
- This simplifies to:
\(
\frac{1}{R_a} = \frac{2}{2} = 1 \implies R_a = 1 \, \Omega
\)
- Now, we connect R3 (which is also 2 Ω) in series with the equivalent resistance Ra:
\(
R_{\text{total}} = R_a + R_3
\)
- Substituting the values:
\(
R_{\text{total}} = 1 \, \Omega + 2 \, \Omega = 3 \, \Omega
\)
- The total resistance of the arrangement is indeed 3 Ω, as required.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C)
22 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(C) MULTIPLE CHOICE TYPE)
2 Videos
- CURRENT ELECTRICITYBOOK - ICSECHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-8(B) (MULTIPLE CHOICE TYPE)
3 Videos
- CALORIMETRYBOOK - ICSECHAPTER - CALORIMETRYEXERCISE - EXERCISE-11(B) (NUMERICALS)
15 Videos
- ELECTRO-MAGNETISM BOOK - ICSECHAPTER - ELECTRO-MAGNETISM EXERCISE - EXERCISE-10 (C) NUMERICALS
1 Video
Similar Questions
Three resistors of 6 Ω, 3Ω and 2Ω are connected together so that the total resistance is greater than 6 Ω, but less than 8 Ω. Draw a diagram to show this arrangement and calculate its total resistance.
View SolutionThree resistors of 2Ω,3Ω and 4Ω are connected in
series
View SolutionYou have three resistors of values 2Ω,3Ωand5Ω. How will you join them so that the total resistance is more than 7Ω?
Draw a diagram for the arrangement.
View SolutionFour resistors each of resistance 2 Ω are connected in parallel. What is the effective resistance ?
View SolutionYou have three resistors of values 2Ω,3Ω and 5 Ω. How will you join them so that the total resistance is less than 1 Ω ? Draw a diagram and find the total resistance.
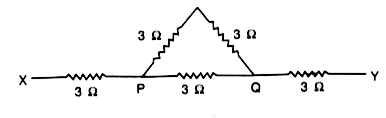
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points X and Y.

View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
View SolutionTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionTwelve resistors each of resistance 1Ω are connected in the circuit shown in figure. Net resistance between point A and H would be

View Solution
