Two resistors of resistances 2Ωand4Ω when connected to a battery will have :
same current flowing through them when connected in parallel
same current flowing through then when connected is series
same potential difference across them when connected is series
different potential difference across them when connected in parallel
The correct Answer is:B
To solve the question regarding the behavior of two resistors of resistances 2Ω and 4Ω when connected to a battery, we will analyze the two configurations: series and parallel.
1. Understanding Series Connection:
- In a series connection, the same current flows through all components. Therefore, if we connect the 2Ω and 4Ω resistors in series, the current I through both resistors will be the same.
- Formula: I=VRtotal, where Rtotal=R1+R2=2Ω+4Ω=6Ω.
2. Understanding Parallel Connection:
- In a parallel connection, the potential difference (voltage) across each resistor is the same, but the current through each resistor can be different.
- The total current I from the battery is divided between the two resistors. The current through each resistor can be calculated using Ohm's Law: I=VR.
- For the 2Ω resistor, I1=V2 and for the 4Ω resistor, I2=V4.
3. Evaluating the Options:
- Option 1: "Same current flowing through them when connected in parallel" - This is incorrect because in parallel, the current is divided.
- Option 2: "Same current flowing through them when connected in series" - This is correct because in series, the current is the same through both resistors.
- Option 3: "Same potential difference across them when connected in series" - This is incorrect because the potential difference across each resistor is different (2I and 4I).
- Option 4: "Different potential differences across them when connected in parallel" - This is incorrect because the potential difference across each resistor is the same in parallel.
4. Conclusion:
- The only correct statement is Option 2: "Same current flowing through them when connected in series".
- In a series connection, the same current flows through all components. Therefore, if we connect the 2Ω and 4Ω resistors in series, the current I through both resistors will be the same.
- Formula: I=VRtotal, where Rtotal=R1+R2=2Ω+4Ω=6Ω.
- In a parallel connection, the potential difference (voltage) across each resistor is the same, but the current through each resistor can be different.
- The total current I from the battery is divided between the two resistors. The current through each resistor can be calculated using Ohm's Law: I=VR.
- For the 2Ω resistor, I1=V2 and for the 4Ω resistor, I2=V4.
- Option 1: "Same current flowing through them when connected in parallel" - This is incorrect because in parallel, the current is divided.
- Option 2: "Same current flowing through them when connected in series" - This is correct because in series, the current is the same through both resistors.
- Option 3: "Same potential difference across them when connected in series" - This is incorrect because the potential difference across each resistor is different (2I and 4I).
- Option 4: "Different potential differences across them when connected in parallel" - This is incorrect because the potential difference across each resistor is the same in parallel.
- The only correct statement is Option 2: "Same current flowing through them when connected in series".
Topper's Solved these Questions
Similar Questions
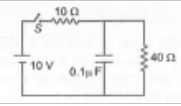
Two resistors of resistances 10Ω and 40Ω are connected with a capacitor of capacitance 0.1μF and ideal battery of emf 10 V. When switch (S) is closed, then initial current and current in steady state through the battery respectively are
View SolutionHow can three resistors of resistances 2Ω,3Ω, and 6Ω be connected to give a total resistance of
(a) 4Ω
(b) 1Ω ?
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionThree resistors 8Ω,12Ωand6Ω are connected to a 12 V battery as shown in Fig. below.

the current through the 8 Ω resistor,
View SolutionThree resistors 8Ω,12Ωand6Ω are connected to a 12 V battery as shown in Fig. below.

the current through the 6Ω resistor.
View SolutionThree resistors 8Ω,12Ωand6Ω are connected to a 12 V battery as shown in Fig. below.

the potential difference across the parallel combination of 6 Ω and 12 Ω resistors,
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power dissipated in each resistor.
View SolutionTwo resistors A and B of resistance 4 Ω and 6 Ω respectively are connected in parallel. The combination is connected across a 6 volt battery of negligible resistance. Calculate :
the power supplied by the battery,
View SolutionThree resistors of 2Ω,3Ω and 4Ω are connected in
series
View Solution
