(a) A current of 1A flows in a series curcuit containing an electric lamp and a conductor of 5Ω when connected to a 10V battery. Calculate the resistance of the electric lamp.
(b) Now if a resistance of 10Ω is connected in parallel with this series combination, what change (if any) in current flowing through 5Ω conductor and potential difference across the lamp will take place ? Give reason.
To solve the given problem step by step, we can break it down into two parts as per the question.
Part (a): Calculate the resistance of the electric lamp.
1. Given Data:
- Current (I) = 1 A
- Voltage (V) = 10 V
- Resistance of the conductor (R_conductor) = 5 Ω
2. Using Ohm's Law:
Ohm's Law states that V=I×R. In a series circuit, the total voltage across the circuit is equal to the sum of the voltage drops across each component.
3. Total Resistance in the Circuit:
The total resistance (R_total) in the circuit can be expressed as:
Rtotal=Rlamp+Rconductor
Where Rlamp is the resistance of the electric lamp.
4. Applying Ohm's Law:
The total voltage across the series circuit can be expressed as:
V=I×Rtotal
Substituting the known values:
10V=1A×(Rlamp+5Ω)
5. Solving for R_lamp:
Rearranging the equation:
10=Rlamp+5
Rlamp=10−5=5Ω
Conclusion for Part (a): The resistance of the electric lamp is 5 Ω.
Part (b): Effect of connecting a 10 Ω resistor in parallel.
1. Understanding the Circuit:
When a 10 Ω resistor is connected in parallel with the series combination of the electric lamp and the 5 Ω conductor, we need to analyze how this affects the current through the 5 Ω conductor and the potential difference across the lamp.
2. Potential Difference Across the Lamp:
The potential difference across the lamp and the 5 Ω resistor remains the same as the voltage of the battery, which is 10 V. This is because they are in series and the voltage across them does not change with the addition of a parallel resistor.
3. Current Through the 5 Ω Conductor:
The current through the 5 Ω resistor can be calculated using Ohm's Law:
I5Ω=VR5Ω=10V5Ω=2A
However, since we have a parallel resistor, we need to consider the total resistance of the circuit.
4. Total Resistance with Parallel Resistor:
The total resistance of the circuit with the 10 Ω resistor in parallel can be calculated using the formula for parallel resistors:
1Rtotal=1Rlamp+Rconductor+1Rparallel
Where Rparallel=10Ω and Rlamp+Rconductor=10Ω.
5. Calculating the New Total Resistance:
1Rtotal=110+110=210=15
Thus, Rtotal=5Ω.
6. Current through the Circuit:
The total current from the battery can be calculated as:
Itotal=VRtotal=10V5Ω=2A
7. Current Distribution:
Since the 10 Ω resistor is in parallel, the voltage across it will also be 10 V. The current through the 10 Ω resistor is:
I10Ω=10V10Ω=1A
Therefore, the remaining current through the 5 Ω resistor will be:
I5Ω=Itotal−I10Ω=2A−1A=1A
Conclusion for Part (b):
- The current flowing through the 5 Ω conductor remains 1 A.
- The potential difference across the lamp remains 10 V.
- Current (I) = 1 A
- Voltage (V) = 10 V
- Resistance of the conductor (R_conductor) = 5 Ω
Ohm's Law states that V=I×R. In a series circuit, the total voltage across the circuit is equal to the sum of the voltage drops across each component.
The total resistance (R_total) in the circuit can be expressed as:
Rtotal=Rlamp+Rconductor
Where Rlamp is the resistance of the electric lamp.
The total voltage across the series circuit can be expressed as:
V=I×Rtotal
Substituting the known values:
10V=1A×(Rlamp+5Ω)
Rearranging the equation:
10=Rlamp+5
Rlamp=10−5=5Ω
When a 10 Ω resistor is connected in parallel with the series combination of the electric lamp and the 5 Ω conductor, we need to analyze how this affects the current through the 5 Ω conductor and the potential difference across the lamp.
The potential difference across the lamp and the 5 Ω resistor remains the same as the voltage of the battery, which is 10 V. This is because they are in series and the voltage across them does not change with the addition of a parallel resistor.
The current through the 5 Ω resistor can be calculated using Ohm's Law:
I5Ω=VR5Ω=10V5Ω=2A
However, since we have a parallel resistor, we need to consider the total resistance of the circuit.
The total resistance of the circuit with the 10 Ω resistor in parallel can be calculated using the formula for parallel resistors:
1Rtotal=1Rlamp+Rconductor+1Rparallel
Where Rparallel=10Ω and Rlamp+Rconductor=10Ω.
1Rtotal=110+110=210=15
Thus, Rtotal=5Ω.
The total current from the battery can be calculated as:
Itotal=VRtotal=10V5Ω=2A
Since the 10 Ω resistor is in parallel, the voltage across it will also be 10 V. The current through the 10 Ω resistor is:
I10Ω=10V10Ω=1A
Therefore, the remaining current through the 5 Ω resistor will be:
I5Ω=Itotal−I10Ω=2A−1A=1A
- The current flowing through the 5 Ω conductor remains 1 A.
- The potential difference across the lamp remains 10 V.
Topper's Solved these Questions
Similar Questions
As electric lamp and a conductor of resistance 4Ω are connected in series to a 6 V battery. The current drawn by the lamp is 0.25 A. Find the resistance of the electric lamp.
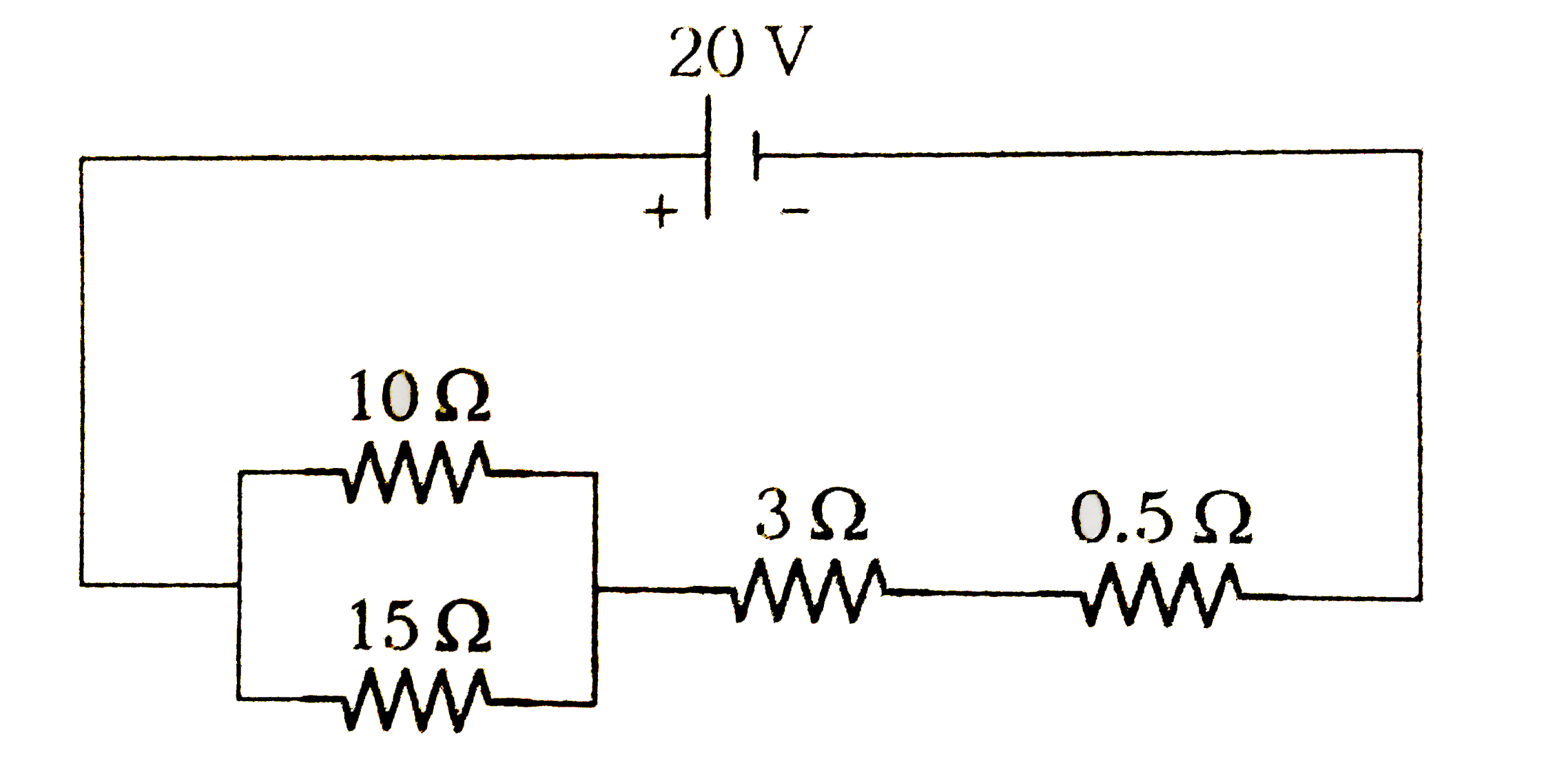
View SolutionIn the circuit, the current flowing through 10Ω resistance is
View SolutionCalculate the current flowing through a wire of resistance 5 Ω connected to a battery of potential difference 3 V.
View SolutionA 6 V, 12 W lamp is connected in series with a resistor R and a source of voltage 12 V.
What is the current flowing through the circuit?
View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View SolutionCalculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionThe current flowing through a lamp marked as 50 W and 250 V is
View Solution6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
View SolutionThe current through tungsten filament lamp connected to a 12 V accumulator of negligible resistance is 3.0 A. Calculate :
the resistance of the filament,
View SolutionAn electric lamp of resistance 2Ω and a conductor of resistance 4Ωare connected to a
6V Battery as shown in the circuit. Calculate:
(a) the totak resistance of the circuit,
(b) the current through the circuit,
(c) the potential difference across the (i) electric lamp
and (ii) conductor, and
(d) power of the lamp.
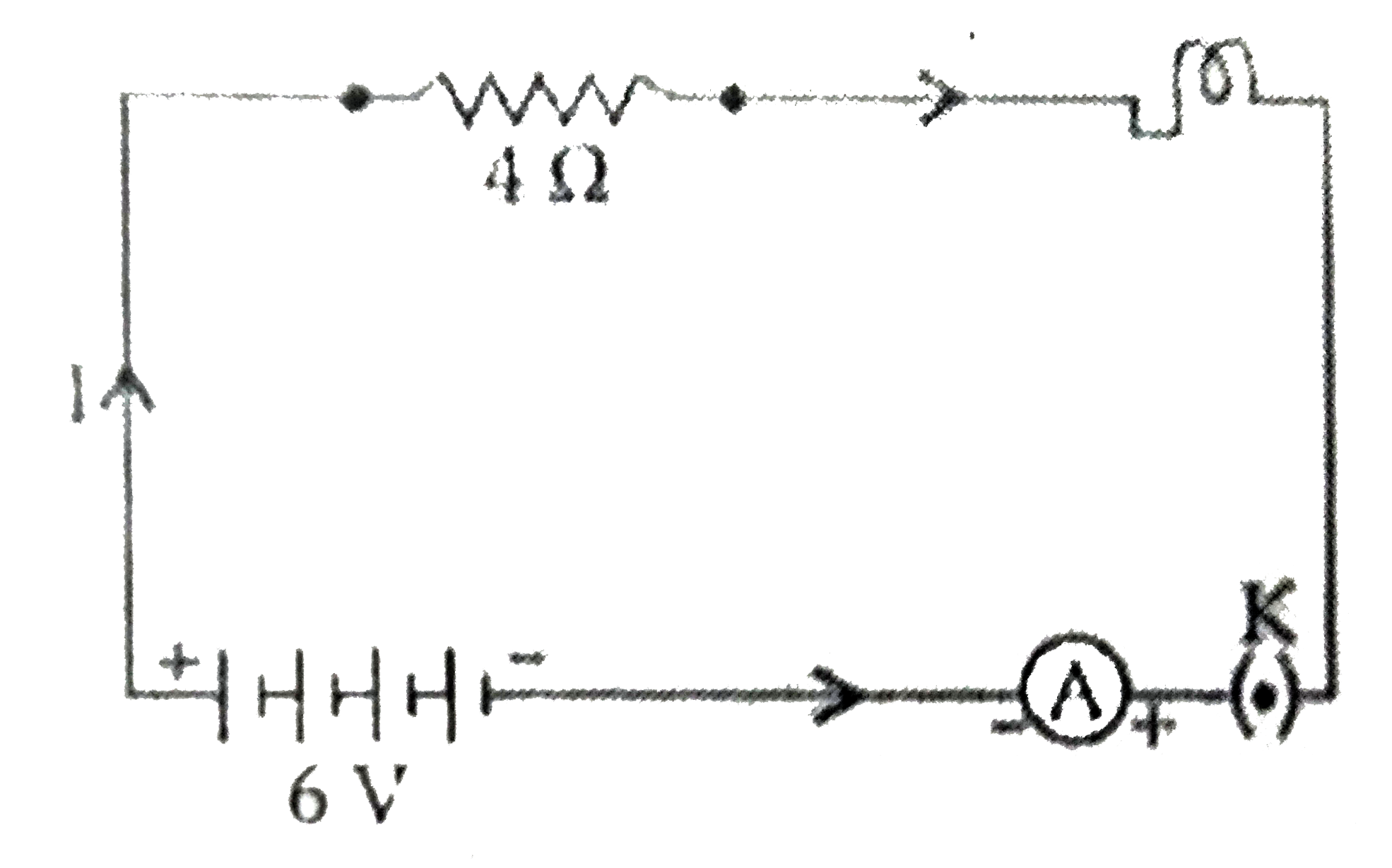
View Solution
