Draw a circuit diagram of an electric circuit containing a cell, a key, an ammeter, a resistance of in series with a combination of two resistors ( each) in parallel and a voltmeter across the parallel combination. Will the potential difference across the resistor be the same as that across the parallel combination of resistors ? Give reason.
Step-by-Step Solution
1. Draw the Circuit Diagram:
- Begin by drawing a cell (battery) with positive and negative terminals.
- Connect a key (switch) in series with the cell.
- Next, connect an ammeter in series with the key.
- After the ammeter, connect a resistor of 2Ω in series.
- Then, create a parallel combination of two resistors, each of 4Ω. Connect these resistors in parallel after the 2Ω resistor.
- Finally, place a voltmeter across the parallel combination of the 4Ω resistors.
Circuit Diagram:
+−−−−(Key)−−−−(Ammeter)−−−−(2Ω)−−−−±−−−(4Ω)−−−−+|∣||±−−−(4Ω)−−−−+|∣±−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−+(Vo<meter)
2. Determine the Equivalent Resistance of the Parallel Resistors:
- For two resistors in parallel, the equivalent resistance \( R_P \) can be calculated using the formula:
\(
\frac{1}{R_P} = \frac{1}{R_1} + \frac{1}{R_2}
\)
- Here, \( R_1 = 4 Ω \) and \( R_2 = 4 Ω \):
\(
\frac{1}{R_P} = \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}
\)
- Therefore, \( R_P = 2 Ω \).
3. Analyze the Potential Difference Across the Resistors:
- The 2Ω resistor is in series with the parallel combination of the 4Ω resistors.
- According to Ohm's Law, the potential difference across a resistor in a series circuit is proportional to its resistance.
- Since the equivalent resistance of the parallel combination is also 2Ω, the potential difference across the 2Ω resistor and the parallel combination will be the same.
4. Conclusion:
- The potential difference across the 2Ω resistor will be the same as that across the parallel combination of the 4Ω resistors because they have the same resistance value and are connected in such a way that they share the same current.
- Begin by drawing a cell (battery) with positive and negative terminals.
- Connect a key (switch) in series with the cell.
- Next, connect an ammeter in series with the key.
- After the ammeter, connect a resistor of 2Ω in series.
- Then, create a parallel combination of two resistors, each of 4Ω. Connect these resistors in parallel after the 2Ω resistor.
- Finally, place a voltmeter across the parallel combination of the 4Ω resistors.
+−−−−(Key)−−−−(Ammeter)−−−−(2Ω)−−−−±−−−(4Ω)−−−−+|∣||±−−−(4Ω)−−−−+|∣±−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−+(Vo<meter)
- For two resistors in parallel, the equivalent resistance \( R_P \) can be calculated using the formula:
\(
\frac{1}{R_P} = \frac{1}{R_1} + \frac{1}{R_2}
\)
- Here, \( R_1 = 4 Ω \) and \( R_2 = 4 Ω \):
\(
\frac{1}{R_P} = \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2}
\)
- Therefore, \( R_P = 2 Ω \).
- The 2Ω resistor is in series with the parallel combination of the 4Ω resistors.
- According to Ohm's Law, the potential difference across a resistor in a series circuit is proportional to its resistance.
- Since the equivalent resistance of the parallel combination is also 2Ω, the potential difference across the 2Ω resistor and the parallel combination will be the same.
- The potential difference across the 2Ω resistor will be the same as that across the parallel combination of the 4Ω resistors because they have the same resistance value and are connected in such a way that they share the same current.
Topper's Solved these Questions
Similar Questions
The potential drop across the 3Ω resistor is
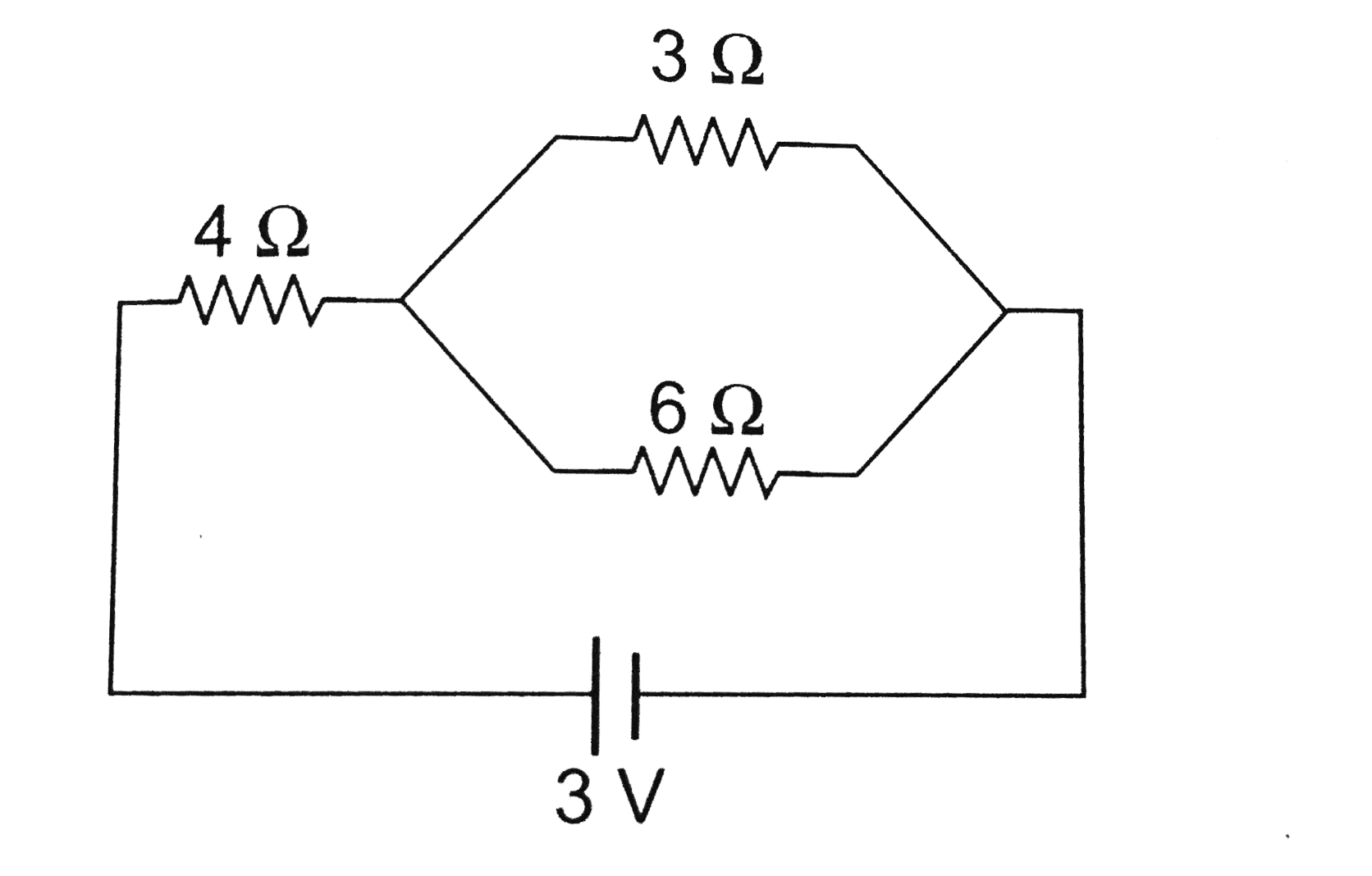
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.
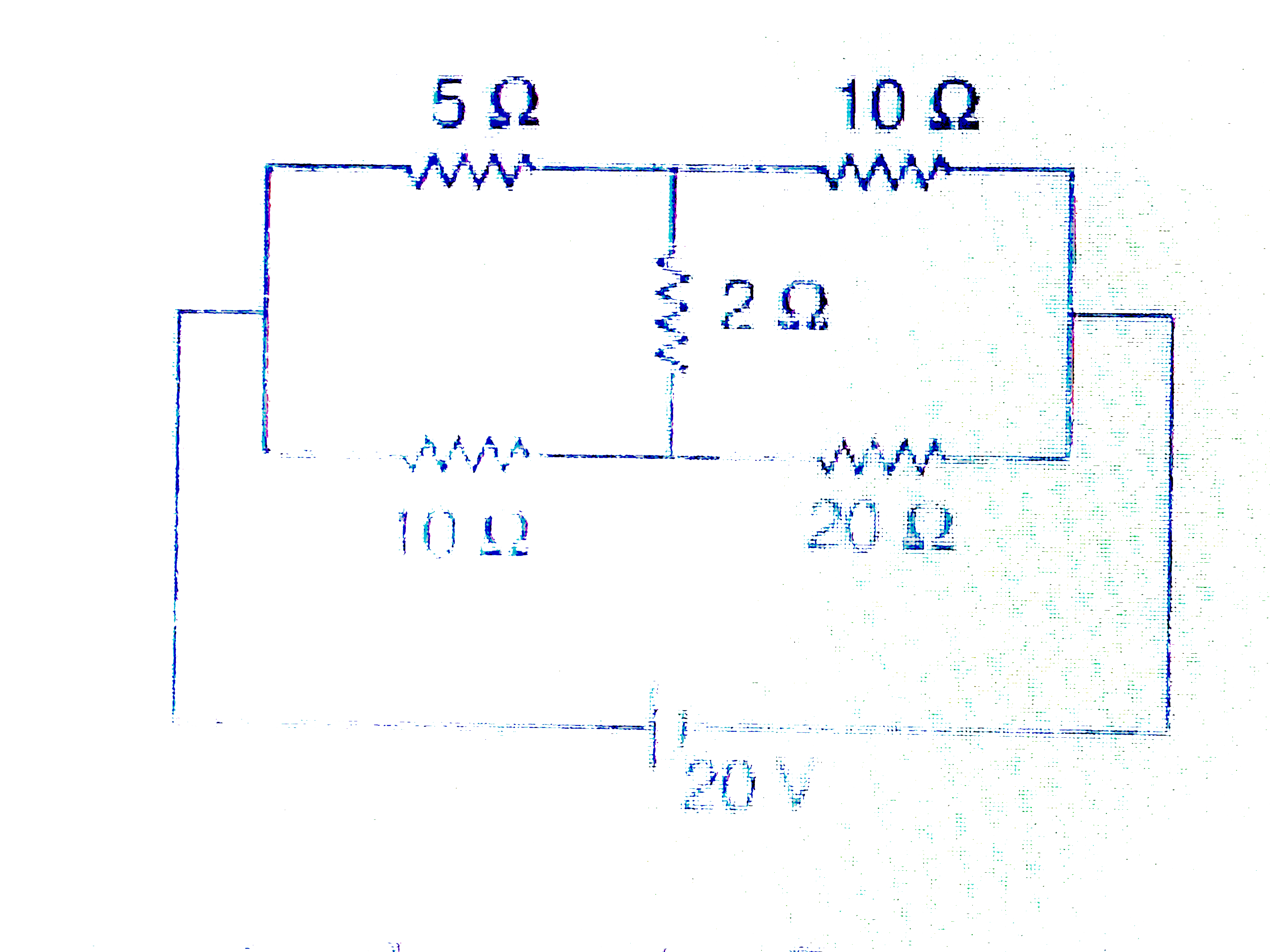
View SolutionIn the given circuit diagram find the potential difference across 2Ω resistance (in volts).
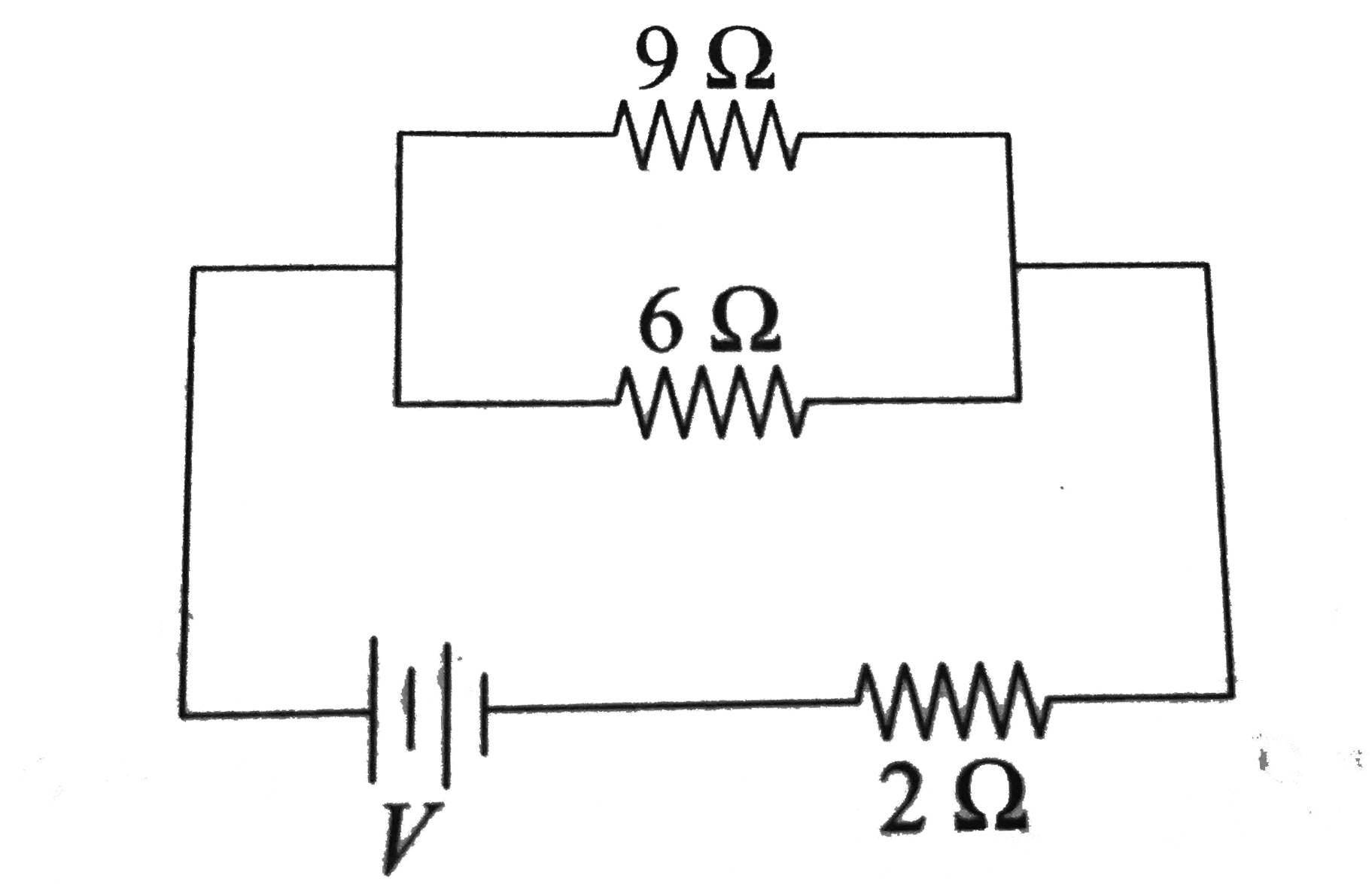
View SolutionIf power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
View SolutionIf the power dissipated in the 27Ω resistor in the circuit shown is 108 watt, the potential difference across the 4Ω resistor is
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View Solution100J of heat are produced each second in a 4Ω resistance. Find the potential difference across the resistor.
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
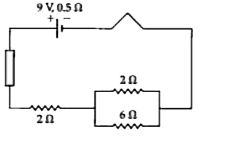
Find
The total resistance
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
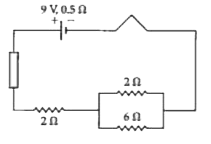
Find
The potential difference across the terminals of the cell.
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View Solution


